Câu hỏi:
26/01/2024 110
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho ^xAy=55o. Hãy tính số đo các góc sau:
^yAt.
Hướng dẫn giải:
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho ^xAy=55o. Hãy tính số đo các góc sau:
^yAt.
Hướng dẫn giải:
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Vì ^xAz và ^yAt là hai góc đối đỉnh nên ^yAt=^xAz=125o.
Hướng dẫn giải:
Vì ^xAz và ^yAt là hai góc đối đỉnh nên ^yAt=^xAz=125o.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
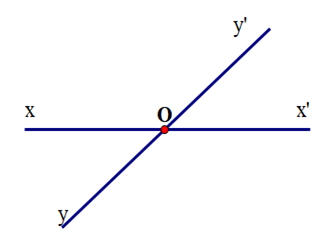
Cho hai đường thẳng xx’ và yy’ cắt nhau như hình vẽ. Biết ^xOy′=2^xOy. Tính ^xOy.
Câu 2:
Cho ^xOy![]() và ^yOz là hai góc kề bù. Biết ^xOy = 60° và tia Ot là tia phân giác của ^yOz. Số đo góc ^xOt là:
và ^yOz là hai góc kề bù. Biết ^xOy = 60° và tia Ot là tia phân giác của ^yOz. Số đo góc ^xOt là:
Câu 3:
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho ^xAy=55o. Hãy tính số đo các góc sau:
^xAz;
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho ^xAy=55o. Hãy tính số đo các góc sau:
^xAz;
Câu 6:
Cho hai đường thẳng xx’ và yy’ cắt nhau như hình vẽ. Biết ^xOy′−^xOy=90o. Tính ^xOy.
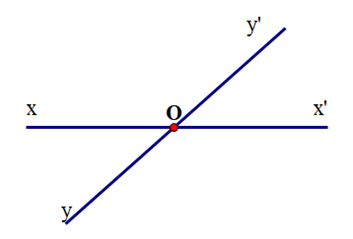
Cho hai đường thẳng xx’ và yy’ cắt nhau như hình vẽ. Biết ^xOy′−^xOy=90o. Tính ^xOy.

Câu 7:
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho ^xOy=60o. Gọi Ot là tia phân giác của ^x′Oy′. Số đo ^xOt là:
Câu 8:
Cho góc bẹt ^aOb. Gọi Oc là tia phân giác của ^aOb; Ox là phân giác của ^aOc; Oy là phân giác của ^cOb. Số đo ^xOy là:
Câu 11:
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho ^xAy=55o. Hãy tính số đo các góc sau:
^zAt;
Cho hai đường thẳng xt và yz cắt nhau tại A sao cho ^xAy=55o. Hãy tính số đo các góc sau:
^zAt;