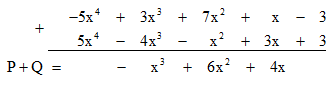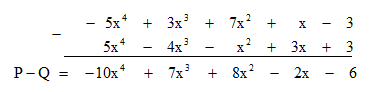Cho hai đa thức P = -5.x^4 + 3.x^3 + 7.x^2 + x - 3 và Q = 5.x^4 - 4.x^3 - x^2 + 3.x + 3

Bài 7.21 trang 35 Toán 7 Tập 2:

Cho hai đa thức P = -5x⁴ + 3x³ + 7x² + x - 3 và Q = 5x⁴ - 4x³ - x² + 3x + 3.

a) Xác định bậc của mỗi đa thức P + Q và P - Q.

b) Tính giá trị của mỗi đa thức P + Q và P - Q tại x = 1; x = -1.

c) Đa thức nào trong hai đa thức P + Q và P - Q có nghiệm là x = 0?

Trả lời

a) Đặt tính cộng P + Q như sau:

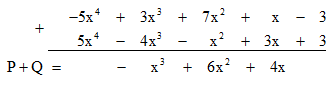
Do đó P + Q = – x³ + 6x² + 4x. Đa thức này có hạng tử bậc cao nhất là – x³ nên bậc của đa thức P + Q là 3.

Đặt tính trừ P – Q như sau:

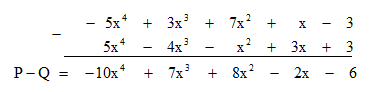
Do đó P – Q = –10x⁴ + 7x³ + 8x² – 2x – 6. Đa thức này có hạng tử bậc cao nhất là -10x⁴ nên bậc của đa thức P – Q là 4.

b) Thay x = 1 vào đa thức P + Q ta có:

P + Q = -1³ + 6 . 1² + 4 . 1 = -1 + 6 + 4 = 9.

Thay x = -1 vào đa thức P + Q ta có:

P + Q = -(-1)³ + 6 . (-1)² + 4 . (-1) = -(-1) + 6 . 1 - 4 = 1 + 6 - 4 = 3.

Thay x = 1 vào đa thức P - Q ta có:

P - Q = -10 . 1⁴ + 7 . 1³ + 8 . 1² - 2 . 1 - 6 = -10 + 7 + 8 - 2 - 6 = -3.

Thay x = -1 vào đa thức P - Q ta có:

P - Q = -10 . (-1)⁴ + 7 . (-1)³ + 8 . (-1)² - 2 . (-1) - 6

          = - 10 . 1 + 7 . (-1) + 8 . 1 + 2 - 6

          = - 10 - 7 + 8 + 2 - 6

          = - 13.

c) Ta thấy đa thức P + Q = – x³ + 6x² + 4x có hệ số tự do bằng 0 nên đa thức P + Q có nghiệm x = 0.

Thay x = 0 vào đa thức P - Q ta có:

P - Q = -10 . 0⁴ + 7 . 0³ + 8 . 0² - 2 . 0 - 6 = -6.

Do đó x = 0 không là nghiệm của đa thức P – Q.

Vậy x = 0 là nghiệm của đa thức P + Q.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 25: Đa thức một biến

Bài 26: Phép cộng và phép trừ đa thức một biến

Luyện tập chung trang 35

Bài 27: Phép nhân đa thức một biến

Bài 28: Phép chia đa thức một biến

Luyện tập chung trang 45