Câu hỏi:
19/12/2023 103Cho góc xOy bằng 60°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = \(4\sqrt 3 \). Tính độ dài đoạn OA để OB có độ dài lớn nhất.
A. \(4\sqrt 3 \);
B. \(3\sqrt 3 \);
C. 3;
D. 4.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D.
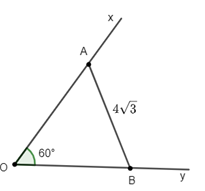
Áp dụng định lý sin trong tam giác OAB ta có:
\(\frac{{OB}}{{\sin \widehat {OAB}}} = \frac{{AB}}{{\sin \widehat {AOB}}}\)
\( \Rightarrow OB = \frac{{AB.\sin \widehat {OAB}}}{{\sin \widehat {AOB}}} = \frac{{4\sqrt 3 .\sin \widehat {OAB}}}{{\sin 60^\circ }} = 8.\sin \widehat {OAB}\).
Mà \(\sin \widehat {OAB} \le 1 \Rightarrow OB \le 8\).
Suy ra maxOB = 8 \( \Leftrightarrow \sin \widehat {OAB} = 1 \Rightarrow \widehat {OAB} = 90^\circ \)
Suy ra tam giác OAB vuông tại A.
Do đó \(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{8^2} - {{\left( {4\sqrt 3 } \right)}^2}} = 4\).
Hướng dẫn giải:
Đáp án đúng là: D.

Áp dụng định lý sin trong tam giác OAB ta có:
\(\frac{{OB}}{{\sin \widehat {OAB}}} = \frac{{AB}}{{\sin \widehat {AOB}}}\)
\( \Rightarrow OB = \frac{{AB.\sin \widehat {OAB}}}{{\sin \widehat {AOB}}} = \frac{{4\sqrt 3 .\sin \widehat {OAB}}}{{\sin 60^\circ }} = 8.\sin \widehat {OAB}\).
Mà \(\sin \widehat {OAB} \le 1 \Rightarrow OB \le 8\).
Suy ra maxOB = 8 \( \Leftrightarrow \sin \widehat {OAB} = 1 \Rightarrow \widehat {OAB} = 90^\circ \)
Suy ra tam giác OAB vuông tại A.
Do đó \(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{8^2} - {{\left( {4\sqrt 3 } \right)}^2}} = 4\).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác DEF có DE = 4 cm; DF = 5 cm và EF = 3 cm. Số đo của của góc D gần nhất với giá trị nào dưới đây?
Câu 2:
Cho tam giác ABC biết \(\frac{{\sin B}}{{\sin C}} = \sqrt 3 \) và \(AB = 2\sqrt 2 \). Tính AC.
Câu 3:
Cho tam giác ABC nhọn biết a = \(\sqrt {24} \), c = \(2 + \sqrt {12} \) và bán kính của đường tròn ngoại tiếp tam giác ABC là R = \(2\sqrt 2 \). Tìm cạnh b của tam giác ABC biết b là số nguyên.
Câu 4:
Cho tam giác ABC có \(\widehat A = 60^\circ \), \(\widehat B = 45^\circ \), b = 4. Tính cạnh a.
Câu 5:
Cho tam giác ABC có BC = 5, CA = 6, AB = 7. Côsin của góc có số đo lớn nhất trong tam giác đã cho là
Câu 6:
Cho tam giác ABC có \(\widehat A = 112^\circ \), AC = 7 và AB = 10. Tính độ dài của cạnh BC và các góc B, C của tam giác đó.
Câu 7:
Cho tam giác ABC biết AB = 4, BC = 6, \(\widehat B = 120^\circ \). Độ dài cạnh AC là
Câu 8:
Cho tam giác ABC có a = 4, b = 6 và cosC = \(\frac{2}{3}\). Giá trị của c bằng:
Câu 9:
Cho tam giác nhọn MNP có \(\widehat N = 60^\circ \); MP = 8 cm; MN = 5 cm. Số đo của góc M gần nhất với giá trị:
Câu 10:
Cho tam giác ABC có \(\widehat A = 120^\circ \), AB = 1, AC = 2. Trên tia CA kéo dài lấy điểm D sao cho BD = 2. Tính AD.


