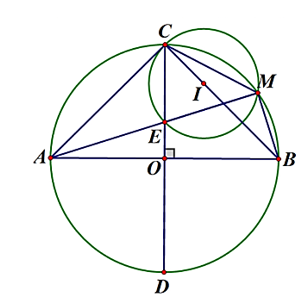
Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Điểm E thuộc OC, nối AE cắt (O) tại M.

a) Chứng minh tứ giác OBME nội tiếp.

Xét đường tròn (O) có AB là đường kính, M thuộc đường tròn

 $\Rightarrow \widehat{AMB}=90°\Rightarrow \widehat{EMB}=90°$

Do AB vuông góc với CD nên ta có: $\widehat{EOB}=90°$

Xét tứ giác OBME có:

$\widehat{EOB}+\widehat{EMB}=90°+90°=180°$

Do đó, tứ giác OBME là tứ giác nội tiếp.