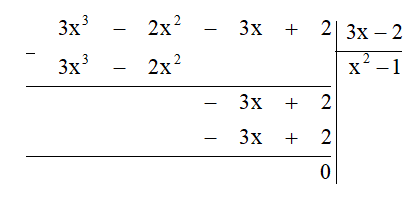Cho đa thức P(x) = 3x^3 – 2x^2 + 5. Chia đa thức P(x) cho đa thức Q(x) (Q(x) ≠ 0) được thương là đa thức S(x) = 3x – 2 và dư là đa thứ

Bài 45 trang 54 SBT Toán 7 Tập 1: 

Cho đa thức P(x) = 3x³ – 2x² + 5. Chia đa thức P(x) cho đa thức Q(x) (Q(x) ≠ 0) được thương là đa thức S(x) = 3x – 2 và dư là đa thức R(x) = 3x + 3. Tìm đa thức Q(x).

Trả lời

Dựa vào quy tắc phép chia ta có:

P(x) = Q(x) . S(x) + R(x)

Hay P(x) – R(x) = Q(x) . S(x)

Suy ra Q(x) = [P(x) – R(x)] : S(x)

Do đó Q(x) = [(3x³ – 2x² + 5) – (3x + 3)] : (3x – 2)

                   = (3x³ – 2x² + 5 – 3x – 3) : (3x – 2)

                   = (3x³ – 2x² – 3x + 2) : (3x – 2)

Ta thực hiện đặt tính chia đa thức như sau:

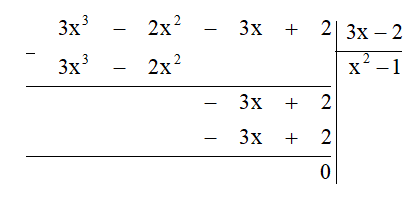
Khi đó Q(x) = (3x³ – 2x² – 3x + 2) : (3x – 2) = x² – 1.

Vậy Q(x) = x² – 1.