Câu hỏi:
21/12/2023 60
Cho bốn tập hợp E, F, G, K thỏa mãn E ⊂ F, F ⊂ G và G ⊂ K. Khẳng định nào sau đây đúng?
Cho bốn tập hợp E, F, G, K thỏa mãn E ⊂ F, F ⊂ G và G ⊂ K. Khẳng định nào sau đây đúng?
A. G ⊂ F;
B. K ⊂ G;
C. E = F = G;
D. E ⊂ K.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
⦁ F ⊂ G nên phương án A sai.
⦁ G ⊂ K nên phương án B sai.
⦁ Giả sử E = {1; 2}, F = {1; 2; 3}, G = {1; 2; 3; 4}.
Ta thấy trong trường hợp trên, ta có E ⊂ F, F ⊂ G nhưng F ⊄ E vì 3 ∈ F nhưng 3 ∉ E.
Do đó phương án C không đúng trong mọi trường hợp.
⦁ Ta có quan hệ bao hàm: E ⊂ F, F ⊂ G và G ⊂ K.
Ta biểu diễn mối quan hệ giữa bốn tập hợp trên biểu đồ Ven như hình bên:
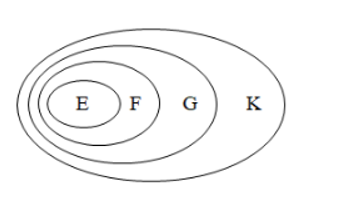
Quan sát biểu đồ Ven, ta thấy E ⊂ K.
Do đó phương án D đúng.
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
⦁ F ⊂ G nên phương án A sai.
⦁ G ⊂ K nên phương án B sai.
⦁ Giả sử E = {1; 2}, F = {1; 2; 3}, G = {1; 2; 3; 4}.
Ta thấy trong trường hợp trên, ta có E ⊂ F, F ⊂ G nhưng F ⊄ E vì 3 ∈ F nhưng 3 ∉ E.
Do đó phương án C không đúng trong mọi trường hợp.
⦁ Ta có quan hệ bao hàm: E ⊂ F, F ⊂ G và G ⊂ K.
Ta biểu diễn mối quan hệ giữa bốn tập hợp trên biểu đồ Ven như hình bên:

Quan sát biểu đồ Ven, ta thấy E ⊂ K.
Do đó phương án D đúng.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho tập hợp A = (– ∞; – 2] và tập B = (– 1; + ∞). Khi đó A ∪ B là:
Câu 5:
Cho tập hợp P = {1; 3} và tập hợp Q = {3; x}. Giá trị của x để P = Q là:
Câu 6:
Cho hai tập hợp A = {x ∈ ℤ| (x2 – 10x + 21)(x3 – x) = 0}, B = {x ∈ ℤ| – 3 < 2x + 1 < 5}. Khi đó tập X = A \ B là:
Cho hai tập hợp A = {x ∈ ℤ| (x2 – 10x + 21)(x3 – x) = 0}, B = {x ∈ ℤ| – 3 < 2x + 1 < 5}. Khi đó tập X = A \ B là:
Câu 7:
Cho mệnh đề: “Nếu hai góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?
Cho mệnh đề: “Nếu hai góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?


