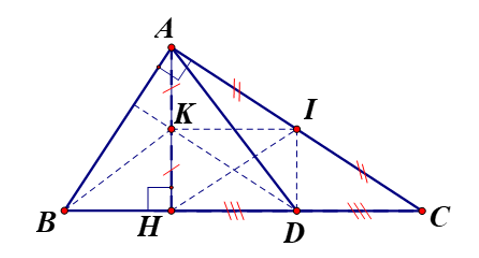
Cho ∆ABC vuông tại A, đường cao AH, lấy I là trung điểm AC. Gọi K và D thứ tự là trung điểm
23
16/11/2024
Cho ∆ABC vuông tại A, đường cao AH, lấy I là trung điểm AC. Gọi K và D thứ tự là trung điểm của AH và HC. Khẳng định nào sau đây là sai?
A. I là giao điểm ba trung trực của ∆AHC;
C. BK ⊥ AD;
D. Cả A, B, C đều sai.
Trả lời
Hướng dẫn giải:
Đáp án đúng là: D
⦁ Trong ∆AHC vuông tại H, dễ dàng chứng minh được
Do đó I cách đều ba đỉnh của tam giác nên I là giao điểm ba trung trực của ∆AHC.
⦁ Ta có AH ⊥ BC, DI ⊥ BC suy ra AH // DI nên (so le trong);
AH ⊥ BC, IK ⊥ AK suy ra IK // BC nên (so le trong).
Xét ∆KHD và ∆DIK có:
KD là cạnh chung;
Do đó ∆KHD = ∆DIK (g.c.g).
Suy ra HK = ID, HD = IK (các cặp cạnh tương ứng)
Xét ∆KDH (vuông tại H) và ∆ICD (vuông tại D) có:
HK = ID (chứng minh trên);
HD = DC (do DI là trung trực của HC).
Do đó ∆KDH = ∆IDC (hai cạnh góc vuông).
Suy ra (hai góc tương ứng)
Mà hai góc này ở vị trí đồng vị nên DK // AC.
Lại có AB ⊥ AC nên DK ⊥ AB
Trong ∆ABD có: AH ⊥ BD (giả thiết), DK ⊥ AB và AH cắt DK tại K
Do đó K là trực tâm ∆ABD, suy ra BK ⊥ AD.