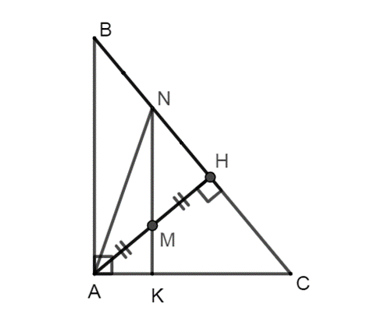
Cho ∆ABC vuông tại A có đường cao AH. Gọi M là trung điểm của AH, qua M kẻ đường thẳng song song với AB. Gọi K là giao điểm của MN và AH.

Cho các khẳng định sau:

(I) CM là đường cao của ∆ANC;

(II) CM ⊥ AN;

(III) NK, AH và CM đồng quy tại M.

 Có bao nhiêu khẳng định đúng?

A. 3;

B. 2;

Hướng dẫn giải:

Đáp án đúng là: A

⦁ Trong ∆ABC có NK // AB mà AB ⊥ AC nên NK ⊥ AC.

Xét ∆ANC có: AH ⊥ NC, NK ⊥ AC và AH và NK giao nhau tại M.

Do đó M là trực tâm của ∆ANC suy ra CM là đường cao của ∆ANC nên CM ⊥ AN.

⦁ Ta có NK, AH và CM là ba đường cao của tam giác ANC nên đồng quy tại M.

Vậy khẳng định (I), (II) và (III) đều đúng. Ta chọn đáp án A.