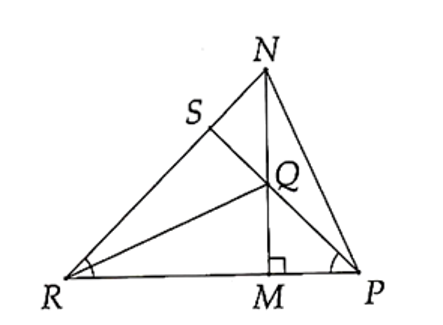
Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP,
Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP, trên tia đối của tia MP lấy điểm R sao cho MR = MN. Gọi S là giao điểm PQ và RN. Cho các khẳng định sau:
(I) PS ⊥ NR;
(II) MN, PS và RQ đồng quy tại Q.
Khẳng định nào sau đây là đúng?
A. Chỉ (I) sai;
B. Chỉ (II) sai;
C. Cả (I), (II) đúng;
D. Cả (I), (II) sai.