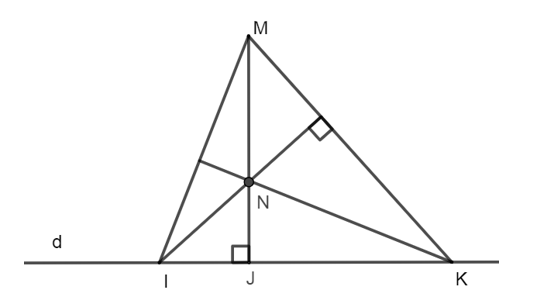
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Khẳng định nào sau đây là đúng?

A. NJ ⊥ MK;

B. MN ⊥ IN;

Hướng dẫn giải:

Đáp án đúng là: C

Ta có: MJ ⊥ IK tại J nên MJ là đường cao của ∆MIK.

Mà N nằm trên đường thẳng qua I và vuông góc với MK nên IN ⊥ MK.

Do đó IN là đường cao của ΔMIK.

Xét ∆MIK có hai đường cao IN và MJ cắt nhau tại N nên N là trực tâm của ΔMIK.

Suy ra KN là đường cao của ∆MIK hay KN ⊥ MI.