Giải các bất phương trình sau: a) 2x^2 + 3x + 1 ≥ 0
Bài 7 trang 61 Toán lớp 10 Tập 1: Giải các bất phương trình sau:
a) 2x2 + 3x + 1 ≥ 0;
b) – 3x2 + x + 1 > 0;
c) 4x2 + 4x + 1 ≥ 0;
d) – 16x2 + 8x – 1 < 0;
e) 2x2 + x + 3 < 0;
g) – 3x2 + 4x – 5 < 0.
Bài 7 trang 61 Toán lớp 10 Tập 1: Giải các bất phương trình sau:
a) 2x2 + 3x + 1 ≥ 0;
b) – 3x2 + x + 1 > 0;
c) 4x2 + 4x + 1 ≥ 0;
d) – 16x2 + 8x – 1 < 0;
e) 2x2 + x + 3 < 0;
g) – 3x2 + 4x – 5 < 0.
a) Xét tam thức bậc hai 2x2 + 3x + 1 có ∆ = 32 – 4 . 2 . 1 = 1 > 0
Suy ra tam thức này có hai nghiệm x1 = – 1, x2 = −12
Ta có hệ số a = 2 > 0.
Khi đó ta có bảng xét dấu sau:
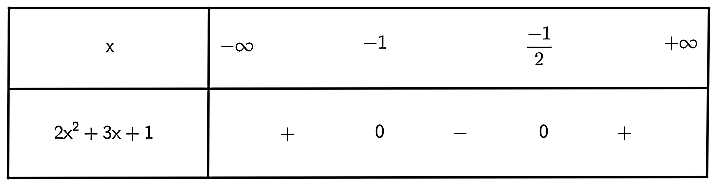
Ta thấy tam thức 2x2 + 3x + 1 không âm khi x ≤ -1 hoặc x≥−12.
Vậy tập nghiệm của bất phương trình đã cho là (−∞;−1]∪[−12;+∞).
b) Xét tam thức bậc hai – 3x2 + x + 1 có: Hệ số a = – 3 < 0 và
∆ = 12 – 4 . (– 3) . 1 = 13 > 0
Suy ra tam thức này có hai nghiệm x1=1−√136,x2=1+√136
Ta có bảng xét dấu sau:
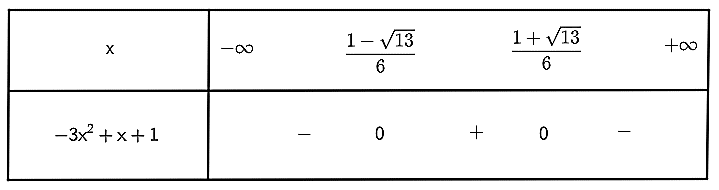
Ta thấy tam thức – 3x2 + x + 1 mang dấu “+” khi x∈(1−√136;1+√136).
Vậy tập nghiệm của bất phương trình – 3x2 + x + 1 > 0 là (1−√136;1+√136).
c) Xét tam thức bậc hai 4x2 + 4x + 1 có hệ số a = 4 > 0 và ∆ = 42 – 4 . 4 . 1 = 0
Suy ra tam thức này có nghiệm kép là x = −12.
Ta có bảng xét dấu sau:
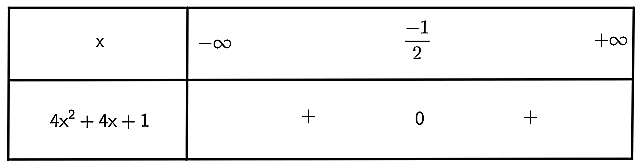
Từ bảng xét dấu ta thấy 4x2 + 4x + 1 > 0 với mọi x≠−12 và 4x2 + 4x + 1 = 0 tại x = −12.
Do đó bất phương trình 4x2 + 4x + 1 ≥ 0 đã cho có vô số nghiệm.
Vậy tập nghiệm của bất phương trình là ℝ.
d) Xét tam thức bậc hai – 16x2 + 8x – 1 < 0 có hệ số a = -16 < 0 và ∆’ = 42 – (– 16) . (– 1) = 0 nên tam thức có nghiệm kép là x = 14.
Ta có bảng xét dấu:
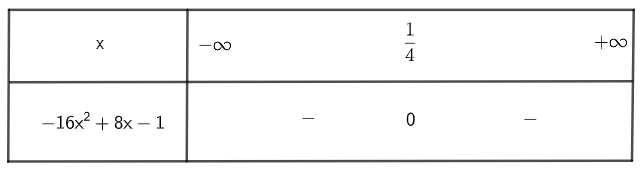
Ta thấy tam thức – 16x2 + 8x – 1 < 0 với mọi x≠14.
Vậy tập nghiệm của bất phương trình – 16x2 + 8x – 1 < 0 là ℝ\{14}.
e) Xét tam thức bậc hai 2x2 + x + 3 có hệ số a = 2 > 0 và ∆ = 12 – 4 . 2 . 3 = – 23 < 0
Ta có bảng xét dấu sau:

Dựa vào bảng xét dấu ta thấy 2x2 + x + 3 > 0 với mọi x∈ℝ.
Vậy bất phương trình 2x2 + x + 3 < 0 vô nghiệm.
g) – 3x2 + 4x – 5 < 0
Xét tam thức bậc hai – 3x2 + 4x – 5 có hệ số a = – 3 < 0 và ∆’ = 22 – (– 3) . (– 5) = – 11 < 0.
Ta có bảng xét dấu:

Dựa vào bảng xét dấu ta thấy – 3x2 + 4x – 5 < 0 với mọi x∈ℝ.
Vậy tập nghiệm của bất phương trình – 3x2 + 4x – 5 < 0 là ℝ.
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 4: Bất phương trình bậc hai một ẩn
Bài 5: Hai dạng phương trình quy về phương trình bậc hai