Cho đồ thị hàm số bậc hai ở Hình 15. a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số

Bài 4 trang 43 Toán lớp 10 Tập 1: Cho đồ thị hàm số bậc hai ở Hình 15.

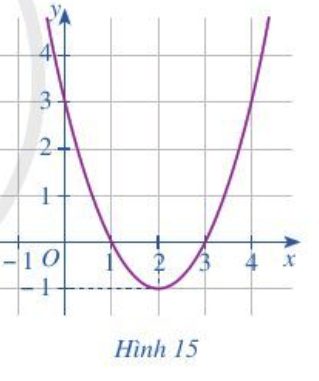
a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.

b) Xác định khoảng đồng biến, khoảng nghịch biến của hàm số. 

c) Tìm công thức xác định hàm số. 

Trả lời

a) Quan sát đồ thị hàm số ở Hình 15, ta thấy trục đối xứng của hàm số là đường thẳng x = 2, tọa độ đỉnh I(2; – 1). 

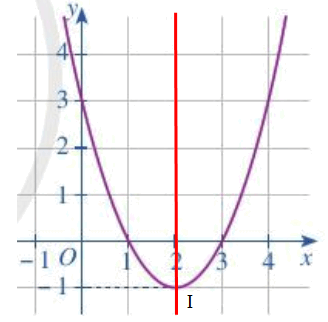
b) Quan sát hình vẽ, ta thấy:

- Đồ thị hàm số đi xuống trên khoảng (– ∞; 2) nên hàm số nghịch biến trên (– ∞; 2).

- Đồ thị hàm số đi lên trên khoảng (2; + ∞) nên hàm số đồng biến trên (2; + ∞).

c) Giả sử hàm số cần tìm có dạng: y = ax² + bx + c   (a ≠ 0) (1)

Đồ thị hàm số cắt trục tung tại (0; 3):

Thay x = 0 và y = 3 vào đồ thị hàm số (1), ta được:

3 = a.0² + b.0 + c ⇔ c = 3.

Đồ thị hàm số cắt trục hoành tại 2 điểm (1; 0) và (3; 0)

Thay x = 1 và y = 0 vào đồ thị hàm số (1), ta được:

0 = a.1² + b.1 + c ⇔ a + b + c = 0

Mà c = 3 nên a + b + 3 = 0

Thay x = 3 và y = 0 vào đồ thị hàm số (1), ta được:

0 = a.3² + b.3 + c ⇔ 9a + 3b + c = 0

Mà c = 3 nên 9a + 3b + 3 = 0

Khi đó ta có hệ phương trình:

$$\begin{gathered} \left\{\begin{array}{l}a+b+3=0\\ 9a+3b+3=0\end{array}\right. \\ \iff \left\{\begin{array}{l}a=-b-3\\ 9\left(-b-3\right)+3b+3=0\end{array}\right. \\ \iff \left\{\begin{array}{l}a=-b-3\\ -6b-24=0\end{array}\right.\iff \left\{\begin{array}{l}a=1\\ b=-4\end{array}\right. \end{gathered}$$

Vậy công thức xác định của hàm số là: y = x² – 4x + 3.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc hai một ẩn

Bài 5: Hai dạng phương trình quy về phương trình bậc hai