Cho tam giác ABC có trung tuyến AM. Chứng minh rằng a) cos góc AMB + cos góc AMC = 0
663
24/05/2023
Bài 3.16 trang 44 Toán 10 Tập 1: Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a) cos^AMB+cos^AMC=0;
b) MA2 + MB2 – AB2 = 2MA.MB.cos^AMB và MA2 + MC2 – AC2 = 2MA.MC.cos^AMC;
c) MA2=2(AB2+AC2)−BC24 (công thức đường trung tuyến).
Trả lời
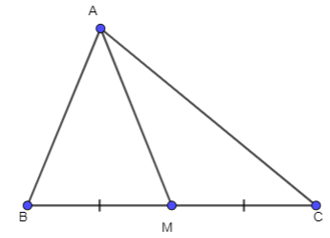
a) Ta có: ^AMB+^AMC=180o
⇒ ^AMC=180o−^AMB
⇒ cos^AMB=−cos(180o−^AMB)=−cos^AMC
⇒ cos^AMB+cos^AMC=−cos^AMC+cos^AMC=0
Vậy cos^AMB+cos^AMC=0 (đpcm)
b) Áp dụng định lí côsin trong ΔAMB, ta có:
AB2 = MA2 + MB2 – 2MA.MB.cos^AMB
⇔ MA2 + MB2 – AB2 = 2MA.MB.cos^AMB (1)
Áp dụng định lí côsin trong ΔAMC, ta có:
AC2 = MA2 + MC2 – 2MA.MC.cos^AMC
⇔ MA2 + MC2 – AC2 = 2MA.MC.cos^AMC (2)
Từ (1) và (2) suy ra điều phải chứng minh.
c) Từ (1) suy ra: MA2 = AB2 – MB2 + 2MA.MB.cos^AMB
Từ (2) suy ra: MA2 = AC2 – MC2 + 2MA.MC.cos^AMC
Cộng vế với vế, ta được:
2MA2 = (AB2 – MB2 + 2MA.MB.cos^AMB) + (AC2 – MC2 + 2MA.MC.cos^AMC)
⇔2MA2 = AB2 + AC2 – MB2 – MC2 + 2MA.MB.cos^AMB + 2MA.MC.cos^AMC
Mà MB=MC=BC2(do AM là trung tuyến) nên:
2MA2 = AB2 + AC2 – (BC2)2 – (BC2)2 + 2MA.MB.cos^AMB + 2MA.MB.cos^AMC
⇔2MA2 = AB2 + AC2 – 2 . (BC2)2 + 2MA.MB.(cos^AMB + cos^AMC)
⇔2MA2 = AB2 + AC2 – BC22
⇔ MA2=AB2+AC2−BC222
⇔MA2=2(AB2+AC2)−BC24 (công thức đường trung tuyến).
Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Bài 6: Hệ thức lượng trong tam giác
Bài tập cuối chương 3
Bài 7: Các khái niệm mở đầu
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vecto với một số

