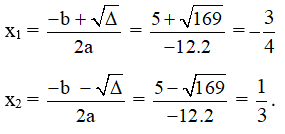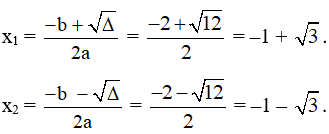Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai  trong mỗi trường hợp sau

Bài 8 trang 10 SBT Toán 10 Tập 2:Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai $f\left(x\right)=x^2+bx+c$ trong mỗi trường hợp sau:

a) Đồ thị của hàm số $f\left(x\right)$ đi qua ba điểm có toạ độ là (– 1; – 4), (0; 3) và (1; –14);

b) Đồ thị của hàm số y = f(x) đi qua ba điểm có toa độ là (0; –2), (2; 6) và (3; 13);

c) f(– 5) = 33, f (0) = 3 và f(2) = l9.

Trả lời

a) Theo đề bài:

Đồ thị của hàm số $y=f\left(x\right)$ đi qua điểm có toạ độ là (– 1; – 4) nên –4 = a – b + c (1)

Đồ thị của hàm số $y=f\left(x\right)$ đi qua điểm có toạ độ là (0; 3) nên 3 = c (2)

Đồ thị của hàm số y = f(x) đi qua điểm có toạ độ là (1; – 14) nên –14 = a + b + c (3)

Thay (2) vào phương trình (1) và (3) ta có:

 $$\begin{gathered} \left\{\begin{array}{l}\text{a}-\text{b}=-7\\ \text{a}+\text{b}=-17\end{array}\right.\iff \left\{\begin{array}{l}2a=-24\\ \text{a}+\text{b}=-17\end{array}\right. \\ \iff \left\{\begin{array}{l}a=-12\\ -12+\text{b}=-17\end{array}\right.\iff \left\{\begin{array}{l}a=-12\\ \text{b}=-5\end{array}\right. \end{gathered}$$

Vậy f (x) = –12x² – 5x + 3.

Xét f ( x ) = –12x² – 5x + 3 có ∆ = (– 5)² – 4.(–12).3 = 169 > 0 nên f (x) có hai nghiệm phân biệt lần lượt là:

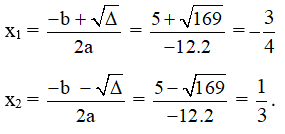
Như vậy, f (x) có a = –12 < 0, ∆ > 0 và có hai nghiệm x₁ = –$\frac{3}{4}$, x₂ = $\frac{1}{3}$  nên:

f (x) dương trong khoảng ( –$\frac{3}{4}$; $\frac{1}{3}$ ).

f (x) âm trong khoảng $\left(-\infty ;\frac{-3}{4}\right)$ và $\left(\frac{1}{3};+\infty \right)$

b) Ta có:

Đồ thị của hàm số $y=f\left(x\right)$ đi qua điểm có toạ độ là (0; – 2) nên –2 = c (1)

Đồ thị của hàm số $y=f\left(x\right)$ đi qua ba điểm có toạ độ là (2; 6) nên 6 = 4a + 2b + c (2)

Đồ thị của hàm số $y=f\left(x\right)$ đi qua ba điểm có toạ độ là (3; 13) nên 13 = 9a + 3b + c (3).

Thay (1) vào phương trình (2) và (3) ta có:

 $$\begin{gathered} \left\{\begin{array}{l}\text{4a + }2\text{b}=8\\ \text{9a}+3\text{b}=15\end{array}\right.\iff \left\{\begin{array}{l}\text{2a + b}=4\\ \text{3a}+\text{b}=5\end{array}\right. \\ \iff \left\{\begin{array}{l}\text{a }=1\\ \text{3.1}+\text{b}=5\end{array}\right.\iff \left\{\begin{array}{l}\text{a }=1\\ \text{b}=2\end{array}\right. \end{gathered}$$

Do đó f (x) = x² + 2x – 2.

Xét f ( x ) = x² + 2x – 2 có ∆ = 2² – 4.( –2 ).1 = 12 nên f ( x ) có hai nghiệm phân biệt lần lượt là:

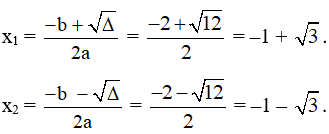
Như vậy, f (x) có a = 1 > 0, ∆ > 0 và có hai nghiệm x₁ = –1 + $\sqrt{3}$, x₂ = –1 – $\sqrt{3}$ nên:

f (x) âm trong khoảng ( –1 – $\sqrt{3}$; –1 + $\sqrt{3}$ ).

f (x) dương trong khoảng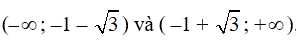 

c) Ta có:

f(– 5) = 33 nên 33 = 25a – 5b + c (1)

f (0) = 3 nên 3 = c (2)

f(2) = 19 nên 19 = 4a + 2b + c (3)

Thay (2) vào phương trình (1) và (3) ta có $\left\{\begin{array}{l}25a-5b=30\\ \text{4a}+2\text{b}=16\end{array}\right.$ . Giải hệ phương trình ta được a = 2 và b =  4.

Vậy f (x) = 2x² + 4x + 3.

Xét f (x) = 2x² + 4x +3 có ∆ = 4² – 4.2.3 = –8 < 0, a = 2 > 0 nên f (x) dương với mọi x ∈ ℝ.

Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài tập cuối chương 6

Bài 1: Dấu của tam thức bậc hai

Bài 2: Giải bất phương trình bậc hai một ẩn

Bài 3: Phương trình quy về phương trình bậc hai

Bài tập cuối chương 7