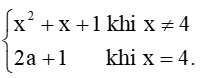a) Với a = 0, xét tính liên tục của hàm số tại x = 4. b) Với giá trị nào của a thì hàm số liên tục tại x = 4
800
16/05/2023
Bài 5 trang 77 Toán 11 Tập 1: Cho hàm số f(x) = 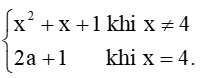
a) Với a = 0, xét tính liên tục của hàm số tại x = 4.
b) Với giá trị nào của a thì hàm số liên tục tại x = 4?
c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?
Trả lời
a) Với a = 0, tại x = 4, ta có:
limx→4f(x)=limx→4(x2+x+1)=42+4+1 = 21 và f(4) = 2.0 + 1 = 1
Suy ra limx→4f(x)≠f(4).
Vì vậy hàm số không liên tục tại x = 4.
b) Ta có: limx→4f(x)=limx→4(x2+x+1)=42+4+1 = 21và f(4) = 2.a + 1
Để hàm số liên tục tại x = 4 thì limx→4f(x) = f(4)
⇔ 21 = 2a + 1
⇔ 2a = 20
⇔ a = 10
Vậy với a = 10 thì hàm số liên tục tại x = 4.
c) Với x ∈ (– ∞; 4) có f(x) = x2 + x + 1 liên tục với mọi x thuộc khoảng này.
Với x ∈ (4; +∞) có f(x) = 2a + 1 liên tục với mọi x thuộc khoảng này.
Tại x = 4 thì a = 10 hàm số liên tục.
Vậy với a = 10 hàm số liên tục trên tập xác định của nó.
Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Giới hạn của dãy số
Bài 2: Giới hạn của hàm số
Bài 3: Hàm số liên tục
Bài tập cuối chương 3