a) Dựa vào định nghĩa của sin α và cos α, hãy tính sin² α + cos² α.

b) Sử dụng kết quả của HĐ6a và định nghĩa của tan α, hãy tính 1 + tan² α.

Lời giải:

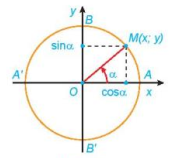
a) Theo định nghĩa, ta có: sin α = y, cos α = x.

Do đó, sin² α + cos² α = (sin α)² + (cos α)² = y² + x².

Từ hình vẽ ta thấy x² + y² = R² = 1 (theo định lí Pythagore và đường tròn đơn vị có bán kính R = 1).

Vậy sin² α + cos² α = 1.

b) Theo định nghĩa với \(\alpha \ne \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\), ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\)

 \( \Rightarrow {\tan ^2}\alpha = {\left( {\frac{{\sin \alpha }}{{\cos \alpha }}} \right)^2} = \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}\).

Do đó, \(1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha + {{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\).

Vậy \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\).