Cách xác định cát tuyến
I. Lý thuyết
1. Khái niệm về cát tuyến
Cát tuyến là một đơn vị kiến thức trong môn hình học được giảng dạy tại chương trình học lớp 9. Cát tuyến là một từ Hán Việt với “cát” có nghĩa là cắt, “tuyến” là đường thẳng, cát tuyến là đường thẳng cắt ngang qua một bề mặt khác như đường cong, đường tròn,… Định nghĩa cát tuyến của đường tròn được nêu trong sách giáo khoa hình học lớp 9 như sau: Cát tuyến của đường tròn chính là đường thẳng cắt đường tròn đó tại 2 điểm phân biệt bất kỳ. Tức là giao điểm giữa đường cát tuyến và đường tròn là hai điểm thuộc đường tròn đó. Trường hợp đặc biệt của cát tuyến chính là đường thẳng đi qua tâm của đường tròn. Khi ấy cát tuyến của đường tròn sẽ trùng với đường kính đường tròn đó. Hay nói cách khác cát tuyến của đường tròn chính là 1 đường thẳng cắt đường tròn đó tại hai điểm phân biệt. Cát tuyến của 2 đường thẳng là 1 đường thẳng cắt 2 đường thẳng trên. Một vài trường hợp đặc biệt đó chính là cát tuyến đi qua tâm đường tròn
Một số ví dụ về đường cát tuyến:
Ví dụ 1: Cát tuyến của hai đường thẳng là một đường thẳng cắt hai đường thẳng đó.
Ví dụ 2: Cát tuyến của đường tròn cắt đường tròn tại hai điểm bất kì thuộc đường tròn đó.
Ví dụ 3: cát tuyến của một cung tròn cắt cung tròn tại hai điểm phân biệt.
Ứng dụng đường cát tuyến hình tròn
Đường cát tuyến hình tròn có thể được sử dụng để giải các bài toán liên quan đến tỉ lệ, tam giác đồng dạng, đường tròn nội tiếp và ngoại tiếp. Một số ví dụ về ứng dụng đường cát tuyến hình tròn là:
- Tính chiều cao của một ngọn núi khi biết góc nhìn từ hai điểm cách nhau một khoảng xác định.
- Tính bán kính của một đường tròn khi biết hai cát tuyến của nó và khoảng cách giữa hai điểm giao của chúng với đường tròn.
- Tính diện tích của một tứ giác nội tiếp trong một đường tròn khi biết các cạnh của nó và các góc tạo bởi các cát tuyến của chúng.
- Tính chiều dài của một cung tròn khi biết hai tiếp tuyến và một cát tuyến của nó
2. Đặc điểm, tính chất đường cát tuyến
Đường cát tuyến là đường thẳng cắt một đường khác (đường thẳng, đường tròn, đường cong,…) tại hai điểm phân biệt. Đường cát tuyến có một số tính chất sau:
- Nếu hai đường thẳng chứa các dây của một đường tròn cắt nhau tại một điểm thì tích các đoạn của mỗi dây bằng nhau.
- Nếu hai đường thẳng cắt nhau tại một điểm và tích các đoạn của mỗi đường bằng nhau thì bốn điểm thuộc cùng một đường tròn.
- Nếu một đường thẳng là tiếp tuyến và một đường thẳng là cát tuyến của một đường tròn thì bình phương của tiếp tuyến bằng tích hai đoạn của cát tuyến.
- Nếu từ một điểm ngoài đường tròn kẻ hai tiếp tuyến và một cát tuyến thì trung điểm của cát tuyến thuộc trung trực của hai tiếp điểm.
- Nếu từ một điểm ngoài đường tròn kẻ hai tiếp tuyến và một cát tuyến thì tỉ số các đoạn của cát tuyến bằng tỉ số các tiếp tuyến
Để có thể nắm rõ được kiến thức và nhận biết được đường cát tuyến thì bạn cần hiểu được bản chất cũng như những tính chất đặc trưng của đường cát tuyến. Đồng thời việc có kiến thức sâu về tính chất đường cát tuyến sẽ giúp các bạn học sinh dễ dàng hơn trong việc giải các bài toán liên quan. Xét trong đường tròn tâm O bán kính R với hai đường thẳng bất kỳ AB và CD. Các tính chất đặc trưng của cát tuyến của một đường tròn bao gồm:
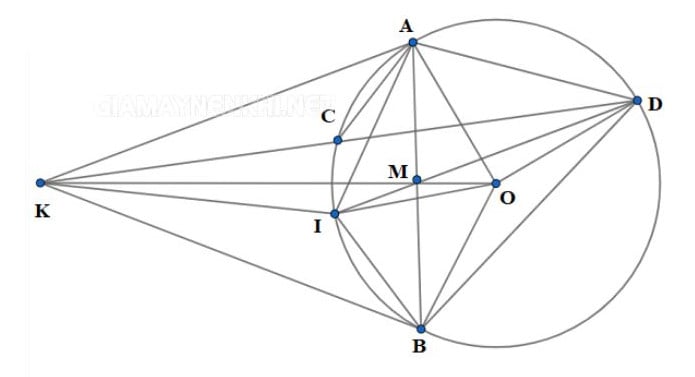
– Trong trường hợp 2 đường thẳng chứa các cung AB và CD của đường tròn tâm O cắt nhau tại điểm M thì ta có biểu thức: MA.MB = MC.MD
– Nếu 2 đường thẳng AB và CD cắt nhau tại điểm M thỏa mãn điều kiện MA.MB = MC.MD thì 4 điểm A, B, C, D sẽ cùng năm trên một đường tròn.
– Nếu MC là đường tiếp tuyến của đường tròn tâm O, MAB là đường cát tuyến thì ta có biểu thức sau đây: MC2 = MA x MB = MO2 – R2
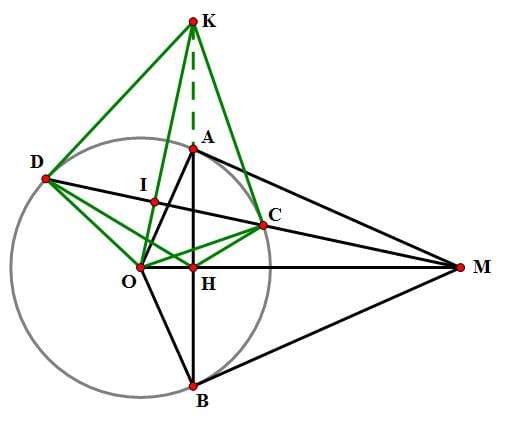
– Kẻ lần lượt các tiếp tuyến KA, KB và cát tuyến KCD từ điểm K nằm ngoài đường tròn. Điểm H là trung điểm của CD thì 5 điểm K, H, A, B, O cùng nằm trên 1 trung điểm.
– Kẻ các tiếp tuyến KA, KB và đường cát tuyến KCD đến đường tròn từ điểm K không thuộc đường tròn thì AC/AD = BC/BD. Bên cạnh đó ta có góc KAC = góc ADK => AC/AD = KC/KA.
3. Cách xác định cát tuyến đường tròn
Cách vẽ đường cát tuyến của đường tròn và đường cong là yêu cầu cơ bản trong bài toán liên quan đến đường cát tuyến. Sau đây chúng tôi sẽ hướng dẫn bạn cách vẽ cát tuyến chỉ với 2 bước đơn giản là:
- Bước 1: Xác định hai điểm bất kì thuộc đường tròn hoặc cung tròn. Lưu ý đối với đường tròn, nếu không có yêu cầu đặc biệt thì bạn không nên chọn hai điểm nằm trên đường kính của đường tròn đó.
- Bước 2: Vẽ một đường thẳng bằng cách nối hai điểm vừa xác định. Đường thẳng này chính là đường cát tuyến, nó cắt và chia đường tròn thành hai cung.
Ngoài ra, bạn cũng có thể dùng các tính chất của cát tuyến để xác định cát tuyến của đường tròn. Một số tính chất quan trọng là: Nếu hai đường thẳng chứa các dây của một đường tròn cắt nhau tại một điểm thì tích các đoạn của mỗi dây bằng nhau. Nếu một đường thẳng là tiếp tuyến và một đường thẳng là cát tuyến của một đường tròn thì bình phương của tiếp tuyến bằng tích hai đoạn của cát tuyến. Nếu từ một điểm ngoài đường tròn kẻ hai tiếp tuyến và một cát tuyến thì tỉ số các đoạn của cát tuyến bằng tỷ số các tiếp tuyến.
II. Bài tập vận dụng
Bài tập 1: Từ điểm M nằm ngoài đường tròn (O) hãy vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O). Ở đây A, B là các tiếp điểm và C nằm giữa M, D.
a) CM: MA.MA = MC.MD.
b) Gọi I là trung điểm của CD. CMR: M, A, O, I, B cùng nằm trên 1 đường tròn.
c) Gọi H là giao điểm của AB và MO. Chứng minh rằng CHOD nội tiếp và AB là đường phân giác của góc CHD.
d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh: A, B, K thẳng hàng
Lời giải:
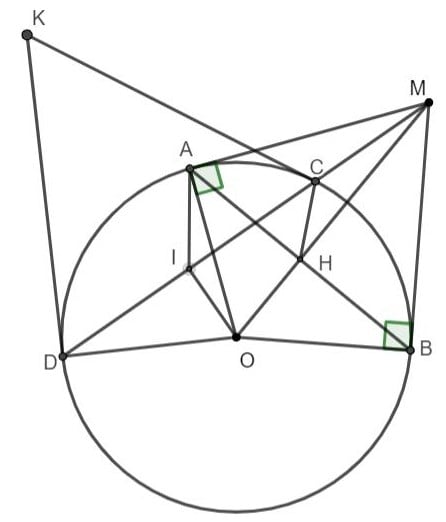
a) Có MA là tiếp tuyến của đường tròn (O) (giả thiết)
→ góc MAC = góc MDA → △ MAC ~ △ MDA (g.g)
→ MA/MD = MC/MA (cặp cạnh tương ứng tỉ lệ) → MA2 = MC.MD (đpcm)
b) Có I là trung điểm của CD (giả thiết)
→ Góc MIO = 900 = góc MAO = MBO
→ 4 điểm M, A, O, I, B cùng thuộc đường tròn đường kính MO.
c) Có MA ⊥ OA, OM ⊥ AB tại H
→ MH. MO = MA2 = MC. MD
→ MA/MD = MC/MA → △ MHC ~ △ MDC
→ góc MHC = góc MDO
→ Tứ giác HCDO nội tiếp đường tròn
→ Góc OHD = góc OCD = góc ODC = góc MHC
→ 900 - góc MHC = 900 - góc OHD → góc CHB = góc BHD
→ HB là phân giác của góc CHD.
d) Có KC và KD là hai tiếp tuyến cắt nhau tại K của đường tròn (O)
→ Tứ giác KCOD nội tiếp đường tròn (hay 4 điểm K, C, O, D cùng thuộc một đường tròn) mà tứ giác HODC nội tiếp đường tròn (chứng minh trên) (hay 4 điểm H, O, D, C cùng thuộc một đường tròn)
→ 5 điểm K, C, H, O, D cùng thuộc một đường tròn
→ HK là phân giác của góc CHD (do KC = KD) → 3 điểm A, B, K thẳng hàng.
Bài tập 3. Từ điểm M nằm ngoài đường tròn (O), vẽ một cát tuyến MCD không đi qua tâm O của đường tròn và hai tiếp tuyến MA, MB đến đường tròn (O). Trong đó A, B là tiếp điểm và C nằm giữa M, D.
a) Chứng minh: MA2 = MC.MD.
b) Lấy I là trung điểm đoạn thẳng CD. Chứng minh 4 điểm M, A, O, I, B cùng nằm trên một đường tròn.
c) Lấy H là giao điểm của hai đoạn thẳng AB và MO. Chứng minh tứ giác CHOD nội tiếp đường tròn và AB là đường phân giác góc CHD.
d) Lấy K là giao điểm của các tiếp tuyến tại hai điểm C và D của đường tròn tâm O. Chứng minh A, B, K thẳng hàng

Bài giải
a)
Theo giả thuyết ta có MA là tiếp tuyến đường tròn (O)
=> góc MAC = góc MDA
=> ΔMAC ~ ΔMDA
=> MCMA = MAMD (cạnh tương ứng tỉ lệ)
Nên MA2 = MC.MD
b)
Theo giả thuyết ta có I là trung điểm CD
=> Góc OIM = 900 = góc OAM = góc OBM
=> M, A, O, I, B cùng nằm trên đường tròn đường kính OM
c)
Ta có MA ⊥ OA; AB ⊥ OM tại H
=> MH. MO = MA2 = MC. MD (chứng minh câu a)
=> MHMC = MOMD => ΔMHC ~ ΔMDO
=> góc MHC = góc MDO
=> Tứ giác HCDO nội tiếp đường tròn
=> Góc OHD = góc ODC = góc OCD = góc MHC
=> 900 - góc MHC = 900 - góc OHD
=> góc CHB = góc BHD
Nên HB là phân giác góc CHD
d)
Ta có 2 tiếp tuyến KC, KD của đường tròn (O) cắt nhau tại K
=> KDOC là tứ giác nội tiếp đường tròn
Theo chứng minh câu c ta có HOHC là tứ giác nội tiếp đường tròn
=> 5 điểm O, D, K, C, H cùng thuộc một đường tròn
=> HK là đường phân giác của góc DHC (vì KC = KD)
Suy ra 3 điểm A, B, K thẳng hàng.
Bài tập 4. Cho 2 đường thẳng song song a, b và một đường cát tuyến c. Hai tia phân giác của cặp góc trong cùng phía cắt nhau tại điểm I. Chứng minh điểm I cách đều 3 đường thẳng a, b và c.

Bài giải
Gọi 3 điểm A, B, C lần lượt là chân đường vuông góc kẻ từ điểm I đến a, b, c.
Xét hai góc trong cùng phía CEA và CFB ta có:
Do I nằm trên tia phân giác của góc CEA nên IA = IC (1)
Do I nằm trên tia phân giác của góc CFB nên IC = IB (2)
Từ (1) và (2) => IA = IB = IC
=> I cách đều đường thẳng a, b và c.
Bài tập 6. Từ điểm K nằm bên ngoài đường tròn tâm O, hãy kẻ các tiếp tuyến KA, KB và kẻ thêm đường cát tuyến KCD đến đường tròn. Lấy M là giao điểm AB và OK. Vẽ đoạn DI đi qua M. Chứng minh:
a) KIOD là tứ giác nội tiếp.
b) KO là đường phân giác góc IKD.

Bài giải
a)
Ta có tứ giác AIBD nội tiếp đường tròn (O) và AB ⋂ ID = M
=> MA.MB = MI.MD (1)
Mặt khác ta có góc KAO = góc KBO = 900 => OBKA là tứ giác nội tiếp
=> MA.MB = MO.MK (2)
Từ (1) và (2) => MI.MD = MO.MK
=> KIOD là một tứ giác nội tiếp
b)
Vì KIOD là tứ giác nội tiếp
Nên góc DKO = góc DIO
góc OKI = góc ODI
Mà ΔDOI cân tại O nên góc DIO = góc DOI
=> góc DKO = góc OKI
Do đó KO là phân giác góc IKD
Bài tập 7. Từ điểm A nằm ngoài đường tròn tâm O, kẻ hai tiếp tuyến AB, AC và một cát tuyến ADE. H là giao điểm AO và BC. Chứng minh H là trung điểm BC.

Bài giải
Xét tứ giác OBAC ta có góc B = góc C = 900 (tính chất tiếp tuyến)
=> góc B + góc C = 1800
Mà hai góc này đối nhau => OBAC nội tiếp đường tròn
Ta có AB = AC (tính chất hai tiếp tuyến của đường tròn cắt nhau)
OB = OC = R
=> O nằm trên đường trung trực của đoạn thẳng BC (1)
Ta có AB = AC (cmt)
=> A nằm trên đường trung trực của đoạn thẳng BC (2)
Từ (1) và (2) => OA là đường trung trực của đoạn BC
hay OA 丄 BC
Ta có ΔOBC cân tại O (OB = OC = R)
Mà OH là đường cao ΔOBC
Nên H là trung điểm BC
Bài tập 8. Từ điểm K ngoài đường tròn tâm O, kẻ hai tiếp tuyến KA, KB và một cát tuyến KCD. Lấy H làm trung điểm CD. Vẽ dây AF đi qua điểm H. Chứng minh BF//CD.

Bài giải
Để chứng minh BF//CD ta cần chứng minh góc AHK = góc AFB (hai góc đồng vị nhau)
Ta có góc AFB = ½ góc AOB (góc nội tiếp chắn cung AB)
Mặt khác ta có KO là đường phân giác góc AOB
=> góc AOK = góc BOK = ½ góc AOB
=> góc AFB = góc AOK
Vì 5 điểm A, K, B, O, H cùng nằm trên đường tròn đường kính KO
Nên góc AHK = góc AOK => góc AFK = góc AHK
Nên BF // CD
Xem thêm các dạng bài tập hay, có đáp án:
20 Bài tập về đường cát tuyến của đường tròn (2024) hay, có đáp án
50 Bài tập Hình Trụ - Hình Nón - Hình Cầu (có đáp án năm 2024)
50 Bài tập Diện tích hình tròn, hình quạt tròn (có đáp án năm 2024)
50 Bài tập Hình cầu. Diện tích mặt cầu và thể tích hình cầu (2024) có đáp án




