50 Bài tập Ôn tập chương 4: Hình Trụ - Hình Nón - Hình Cầu (có đáp án năm 2024) - Toán 9

Hình Trụ - Hình Nón - Hình Cầu

Kiến thức cần nhớ

1. Hình trụ

a) Định nghĩa

Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB cố định, ta được một hình trụ.

- Hai hình tròn (A) và (B) bằng nhau và nằm trong hai mặt phẳng song song được gọi là hai đáy của hình trụ.

- Đường thẳng AB được gọi là trục của hình trụ.

- Mỗi vị trí của CD được gọi là một đường sinh. Các đường sinh vuông góc với hai mặt phẳng đáy. Độ dài của đường sinh là chiều cao của hình trụ.

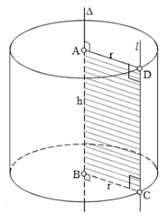
b) Cắt hình trụ bởi một mặt phẳng

- Khi cắt hình trụ bởi một mặt phẳng song song với đáy, thì phần mặt phẳng nằm trong hình trụ (mặt cắt – thiết diện) là một hình tròn bằng hình tròn đáy.

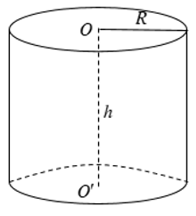
c) Công thức diện tích và thể tích hình trụ

Cho hình trụ có bán kính đáy R và chiều cao h.

- Diện tích xung quanh: S_xq = 2πRh.

- Diện tích toàn phần: S_tp = 2πRh + 2πR².

- Thể tích: V = πR²h.

2. Hình nón

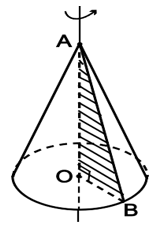
a) Định nghĩa

Khi quay tam giác vuông AOC một vòng quanh cạnh OA cố định thì được một hình nón.

- Điểm A được gọi đỉnh của hình nón.

- Hình tròn (O) được gọi là đáy của hình nón.

- Mỗi vị trí của AC được gọi là một đường sinh của hình nón.

- Đoạn AO được gọi là đường cao của hình nón.

b) Công thức tính diện tích và thể tích của hình nón

Đặt AC = l; l là đường sinh.

Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.

- Diện tích xung quanh: S_xq = πRl.

- Diện tích toàn phần: S_tp = πRl + πR².

- Thể tích: $V=\frac{1}{3}\pi R^{2}h$.

3. Hình nón cụt

a) Định nghĩa

Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần hình nón nằm giữa mặt phẳng nói trên và mặt phẳng đáy được gọi là một hình nón cụt.

- Hai hình tròn (O) và (O') được gọi là hai đáy.

- Đoạn OO' được gọi là trục. Độ dài OO' là chiều cao.

- Đoạn AC được gọi là đường sinh.

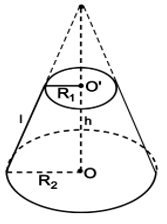
b) Công thức tính diện tích và thể tích hình nón cụt

Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.

- Diện tích xung quanh: S_xq = π (R + r) l.

- Thể tích: $V=\frac{1}{3}\pi h(R^2+Rr+r^2)$.

4. Hình cầu

a) Định nghĩa

Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.

- Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu.

- Điểm O được gọi tâm, R là bán kính của hình cầu hay mặt cầu đó.

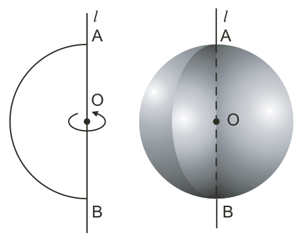
b) Cắt hình cầu bởi một mặt phẳng

Khi cắt hình cầu bởi một mặt phẳng ta được một hình tròn.

Khi cắt mặt cầu bán kính R bởi một mặt phẳng ta được một đường tròn:

- Đường tròn đó có bán kính R nếu mặt phẳng đi qua tâm (gọi là đường tròn lớn).

- Đường tròn đó có bán kính bé hơn R nếu mặt phẳng không đi qua tâm.

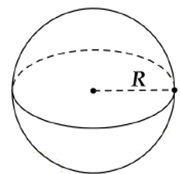
c) Công thức tính diện tích và thể tích hình cầu

Bài tập tự luyện

Bài 1. Cho hình trụ có bán kính đáy R =12 cm và diện tích toàn phần 672 cm². Tính chiều cao của hình trụ.

Lời giải:

Diện tích toàn phần của hình trụ là: 24πh + 2π . 12² = 672 π

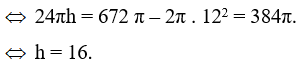
Vậy chiều cao của hình trụ là 16 cm.

Bài 2. Cho hình trụ bị cắt bỏ một phần OABB’A’O’ như hình vẽ. Tính thể tích phần còn lại.

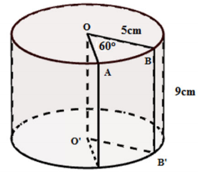
Lời giải:

Phần hình trụ bị cắt đi chiếm $\frac{{60}^o}{{360}^o}=\frac{1}{6}$ (hình trụ)

Thể tích phần còn lại là: V = $\frac{5}{6}\pi R^{2}h=\frac{5}{6}\pi .5^2.9$ = 187,5π (cm³).

Vậy thể tích phần còn lại là 187,5π cm³.

Bài 3. Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy S = 25π cm² và chiều cao h = 10 cm. Nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?

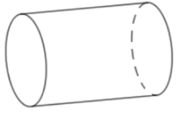
Lời giải:

Bán kính R của đường tròn đáy là πR² = 25π$\iff$ R = 5 cm.

Diện tích xung quanh của hình trụ là:

S_xq = 2πRh = 2π . 5 . 10 = 100 (cm²)

Vì trục lăn 12 vòng nên diện tích tạo trên sân phẳng là:

12 . 100π  = 1200π (cm²)

Vậy nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là 1200π cm².

Bài 4. Mặt cắt chứa trục của một hình nón là một tam giác đều có diện tích $9\sqrt{3}$cm². Tính thể tích của hình nón đó.

Lời giải:

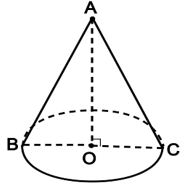
Gọi mặt cắt là tam giác đều ABC, đáy của hình nón có tâm là O.

Ta đặt AB = AC = BC = a thì bán kính đáy hình nón là $R=\frac{a}{2}$ và chiều cao của hình nón là $h=\frac{a\sqrt{3}}{2}$.

Vì diện tích của tam giác đều là $9\sqrt{3}$ cm² nên ta có:

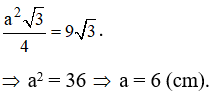
Do đó bán kính đáy là R = 3 cm và chiều cao hình nón là:

$h=\frac{6\sqrt{3}}{2}=3\sqrt{3}$(cm)

Thể tích của hình nón là:

$V=\frac{1}{3}\pi R^{2}h$$=\frac{1}{3}\pi .3^2.3\sqrt{3}=9\sqrt{3}\pi$ (cm³)

Vậy thể tích của hình nón là: $9\sqrt{3}$ cm³.

Bài 5. Một hình nón cụt có các bán kính đáy là 21 cm và 49 cm. Biết diện tích xung quanh của nó là 3710π cm². Tính thể tích của hình nón cụt.

Lời giải:

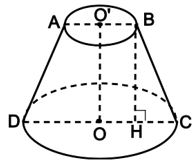
Gọi mặt cắt chứa trục của hình nón cụt là hình thang cân ABCD.

Trong mặt phẳng này vẽ $BH\perp CD$.

Ta đặt O’B= R₁, OC = R₂, OO’ = h và BC = 1.

Ta có: BH = OO’ = h; HC = R₂ – R₁ = 49 – 21 = 28 (cm).

Vì diện tích xung quanh của hình nón cụt là 3710π cm² nên:

π(R₁  +R₂)l = 3710π

Suy ra: $l=\frac{3710\pi }{\pi (21+49)}=53$  (cm)

Xét ∆BHC vuông tại H, ta có:

$BH=\sqrt{B{C}^2-H{C}^2}$$=\sqrt{{53}^2-{28}^2}=45\left(cm\right)$

Thể tích của hình nón cụt là:

$$\begin{gathered} V=\frac{1}{3}\pi h(R_1^2+R_2^2+R_1{R}_2) \\ =\frac{1}{3}\pi .45({21}^2+{49}^2+21.49) \\ =58065\pi \left(c{m}^3\right) \end{gathered}$$

Vậy thể tích của hình nón cụt là 58 065π cm³.

Bài 6. Một chao đèn có dạng mặt xung quanh của một hình nón cụt. Các bán kính đáy lần lượt là R1 = 5 cm, R2 = 13 cm. Biết diện tích xung quanh của chao đèn là 306π cm². Tính chiều cao của chao đèn.

Lời giải:

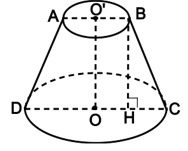
Gọi mặt cắt chứa trục của chao đèn là hình thang cân ABCD.

Chiều cao OO’ = h và đường sinh BC = l.

Vì diện tích xung quanh của chao đèn là 306π cm² nên ta có:

π(R₁ + R₂)l = 306 π

$\Rightarrow$ π(5 + 13)l = 306 π

$\Rightarrow$ l = 17 (cm)

Trong mặt phẳng ABCD ta vẽ $BH\perp CD$.

Ta có BH = OO’ = h; OH = O’B = R₁.

Do đó HC = R₂ – R₁ = 8 (cm).

Xét ∆BHC vuông tại H, ta có:

$BH=\sqrt{B{C}^2-H{C}^2}$$=\sqrt{{17}^2-8^2}=15$ (cm)

Vậy chiều cao của chao đèn là 15 cm.

Bài 7. Hai hình cầu có hiệu các bán kính bằng 3 cm và hiệu các thể tích bằng 1332π cm³. Tính hiệu các diện tích của hai mặt cầu.

Lời giải:

Gọi bán kính của hình cầu lớn là R và bán kính của hình cầu nhỏ là r.

Ta có R – r = 3 hay R = r + 3.

Nên:

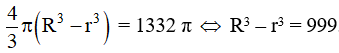
Do đó (r + 3)³ – r³ = 999$\iff$  r² + 3r – 108 = 0.

Giải ra được r₁ = –12 (loại), r₂ = 9 (chọn).

Do đó bán kính hình cầu nhỏ là 9 cm, bán kính hình cầu lớn là 12 cm.

Diện tích mặt cầu lớn là:

S₁ = 4πR² = 4π . 12² = 576π (cm²).

Diện tích mặt cầu nhỏ là:

S₂ = 4πr² = 4π . 9² = 324π (cm²).

Hiệu diện tích hai mặt cầu là:

S = S₁ – S₂ = 576π – 324π = 252π (cm²)

Vậy hiệu diện tích hai mặt cầu là 252π cm².

Bài 8. Một hình cầu có bán kính bằng bán kính đáy của một hình nón. Biết đường sinh của hình nón bằng 12 cm và diện tích xung quanh của hình nón bằng diện tích mặt cầu. Tính thể tích hình cầu.

Lời giải:

Gọi bán kính hình cầu cũng như bán kính đáy hình nón là R.

Diện tích xung quanh hình nón là: πRl = 12πR.

Diện tích mặt cầu là: 4πR².

Vì diện tích xung quanh hình nón bằng diện tích mặt cầu nên:

12πR = 4πR² $\Rightarrow$ R = 3 (cm).

Thể tích hình cầu là: $V=\frac{4}{3}\pi R^3$$=\frac{4}{3}\pi .3^3=36\pi$ (cm³).

Vậy thể tích hình cầu là 36π cm³.

Bài 9. Cho một hình cầu nội tiếp một hình trụ. Chứng minh rằng:

a) Thể tích hình cầu bằng $\frac{2}{3}$ thể tích hình trụ;

b) Diện tích mặt cầu bằng $\frac{2}{3}$ diện tích toàn phần hình trụ.

Lời giải:

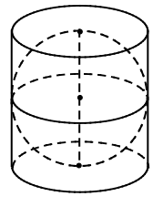
Gọi bán kính hình cầu là R thì bán kính đáy hình trụ là R và chiều cao hình trụ là 2R.

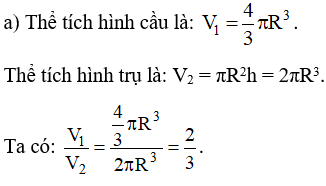
Vậy thể tích hình cầu bằng $\frac{2}{3}$ thể tích hình trụ.

b) Diện tích mặt cầu là: S₁ = 4πR².

Diện tích hình trụ là: S₂ = 2πR(h + R) = 2πR(2R + R) = 6πR².

Ta có: $\frac{S_1}{S_2}=\frac{4\pi R^2}{6\pi R^2}=\frac{2}{3}$.

Vậy diện tích mặt cầu bằng $\frac{2}{3}$ diện tích toàn phần hình trụ.

Xem thêm các dạng bài tập liên quan khác:

60 Bài tập về khối đa diện lồi và khối đa diện đều ( có đáp án năm 2023 )

60 Bài tập về mặt cầu (có đáp án năm 2023)

60 Bài tập khái niệm về mặt tròn xoay (có đáp án năm 2023)

60 Bài tập về phương trình mặt phẳng (có đáp án năm 2023)

60 Bài tập về phương trình đường thẳng trong không gian (có đáp án năm 2023)