Cách vẽ và bài tập parabol dễ hiểu nhất (2024)

Cách vẽ đồ thị Parabol

I. Lí thuyết tổng hợp

- Tập xác định của phương trình Parabol: $D=ℝ$

- Trục đối xứng của Parabol: là đường thẳng đi qua đỉnh của Parabol và song song với trục Oy có phương trình $x=\frac{-b}{2a}$

- Đồ thị Parabol có hai dạng:

+) Dạng 1: a > 0 (bề lõm của đồ thị hướng lên trên)

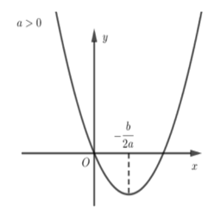
Hàm số $y=a{x}^2+bx+c$ đồng biến trên khoảng $\left(\frac{-b}{2a};+\infty \right)$ và nghịch biến trên khoảng $\left(-\infty ;\frac{-b}{2a}\right)$.

+)  Dạng 2: a < 0 (bề lõm của đồ thị hướng xuống dưới)

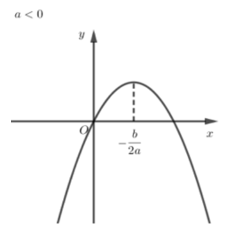
Hàm số $y=a{x}^2+bx+c$ nghịch biến trên khoảng $\left(\frac{-b}{2a};+\infty \right)$ và đồng biến trên khoảng $\left(-\infty ;\frac{-b}{2a}\right)$.

1.Cách vẽ parabol bằng hàm bậc 2

Cách vẽ đồ thị Parabol: $y=a{x}^2+bx+c$

Bước 1: Vẽ trục đối xứng có phương trình $x=\frac{-b}{2a}$.

Bước 2: Xác định tọa độ đỉnh : $I\left(\frac{-b}{2a};\frac{-\Delta }{4a}\right)$

Bước 3: Xác định thêm 1 số điểm (tối thiểu 1 điểm) như giao điểm với trục tung   M (0; c) (nếu có), trục hoành (nếu có) hoặc các điểm tùy ý.  Sau đó lấy điểm đối xứng với các điểm điểm đó qua trục đối xứng.

Bước 4: Vẽ đồ thị bằng cách nối các điểm lại theo dạng hình Parabol.

Lưu ý: Khi vẽ parabol y = ax² + bx + c (a ≠ 0) cần chú ý đến dấu của hệ số a (a > 0 bề lõm quay lên trên còn a < 0 bề lõm quay xuống dưới).

2.Cách vẽ parabol bằng thước và compa

Bước 1: Khảo sát các điểm thuộc Parabol (Vì Parabol là hình đối xứng nên chúng ta chỉ cần khảo sát 1 nửa hình Parabol).

Bước 2: Xác định trục đối xứng của Parabol (kẻ đường thẳng đi qua điểm F cho trước và vuông góc với đường chuẩn), gọi giao điểm là O.

Bước 3: Lấy M là trung điểm của OF, chọn một điểm M₁  bất kỳ thuộc đoạn MF, kẻ đường thẳng đi qua M₁  và song song với đường thẳng cho trước.

Bước 4: Dùng Compa, quay 1 cung có bán kính OM₁ , cung và đường thẳng qua OM₁  cắt nhau ở đâu, ta được 1 điểm thuộc Parabol.

Bước 5: Lấy thêm các điểm bất kỳ thuộc đoạn MF rồi làm tương tự các bước trên, nối các điểm thuộc Parabol, ta được hình Parabol hoàn chỉnh.

3.Ví dụ minh họa

Bài 1: Vẽ đồ thị Parabol: $y=x^2-4x+5$.

Lời giải:

- Tập xác định: $D=ℝ$

- Ta có trục đối xứng của đồ thị: $x=\frac{-(-4)}{2.1}=2$

- Xét $\Delta ={(-4)}^2-\mathrm{4.1.5}=-4$ Tọa độ đỉnh I của Parabol:

$$\begin{gathered} x_I=\frac{-(-4)}{2.1}=2 \\ {y}_I=\frac{-(-4)}{4.1}=1 \end{gathered}$$

$\Rightarrow$ I (2; 1)

- Giao điểm của Parabol với trục tung: A (0; 5). Lấy thêm điểm A’(4; 5) đối xứng với A qua trục đối xứng.

- Có a = 1 > 0 , trục đối xứng x = 2 và các điểm I (2; 1), A (0; 5), A’(4; 5) ta vẽ được đồ thị:

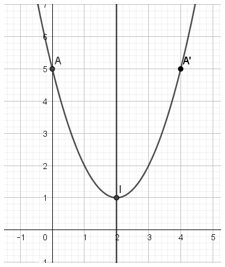
Bài 2: Vẽ đồ thị Parabol:$y=-x^2-3x+4$

Lời giải:

- Tập xác định: $D=ℝ$

- Ta có trục đối xứng của đồ thị:$x=\frac{-(-3)}{2.(-1)}=\frac{-3}{2}$

- Xét $\Delta ={(-3)}^2-4.(-1).4=25\Rightarrow$ Tọa độ đỉnh I của Parabol:

$$\begin{gathered} x_I=\frac{-(-3)}{2.(-1)}=\frac{-3}{2} \\ {y}_I=\frac{-25}{4.(-1)}=\frac{25}{4} \end{gathered}$$

$\Rightarrow$ I$\left(\frac{-3}{2};\frac{25}{4}\right)$

- Giao điểm của Parabol với trục tung: B (0; 4). Lấy thêm điểm B’(-3; 4) đối xứng với B qua trục đối xứng.

- Có a = -1 < 0 , trục đối xứng $x=\frac{-3}{2}$ và các điểm I$\left(\frac{-3}{2};\frac{25}{4}\right)$ , B (0; 4), B’(-3; 4) ta vẽ được đồ thị:

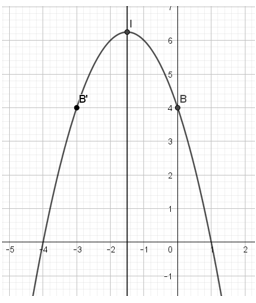
Bài 3: Vẽ đồ thị Parabol:$y=x^2-4x+4$ . Xét tính đồng biến, nghịch biến của nó trên tập xác định.

Lời giải:

- Tập xác định: $D=ℝ$

- Ta có trục đối xứng của đồ thị: $x=\frac{-(-4)}{2.1}=2$

- Xét $\Delta ={(-4)}^2-\mathrm{4.1.4}=0\Rightarrow$ Tọa độ đỉnh I của Parabol:

$$\begin{gathered} x_I=\frac{-(-4)}{2.1}=2 \\ {y}_I=\frac{0}{4.1}=0 \end{gathered}$$

$\Rightarrow$ I (2; 0)

- Giao điểm của Parabol với trục tung: C(0; 4). Lấy thêm điểm C’(4; 4) đối xứng với C qua trục đối xứng.

- Có a = 1 > 0 , trục đối xứng x = 2 và các điểm I (2; 0) , C (0; 4), C’(4; 4) ta vẽ được đồ thị:

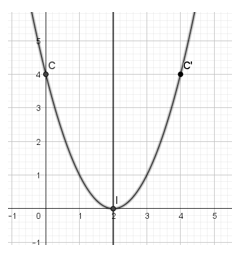
- Dựa vào đồ thị ta có thể thấy, hàm số $y=x^2-4x+4$ đồng biến trên khoảng $(2;+\infty )$ và  nghịch biến trên khoảng $(-\infty ;2)$.

Bài 4: Khảo sát và vẽ đồ thị hàm số y = –x² + 4x – 4.

Lời giải:

Xét hàm số y = –x² + 4x – 4.

• Tập xác định hàm số: R
• Đỉnh parabol: I (2; 0)
• Trục đối xứng: x = 2.
• Giao điểm parabol với trục hoành: A(2; 0).
• Giao điểm parabol với trục tung: B(0; –4).
• Điểm đối xứng với điểm B(0; –4) qua đường thẳng x = 2 là C(4; –4).

Bảng biến thiên:

Đồ thị hàm số:

II. Bài tập vận dụng (có đáp án)

Bài 1: Vẽ đồ thị hàm số y = $x^2$.

Lời giải:

Tập xác định của hàm số là: $D=ℝ$

Bảng giá trị tương ứng của x và y

Trên mặt phẳng tọa độ Oxy, lấy các điểm O(0; 0), A(1; 1), B(2; 4), C(3; 9) và A’(-1; 1), B’(-2; 4), C’(-3; 9) rồi lần lượt nối chúng theo đường cong parabol.

Ta có đồ thị hàm số y = $x^2$.

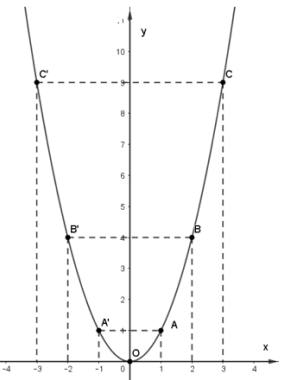
Bài 2: Cho hàm số y = -$x^2$.  Vẽ đồ thị hàm số y = -$x^2$

Lời giải:

Tập xác định của hàm số là: $D=ℝ$

Bảng giá trị tương ứng của x và y

Trên mặt phẳng tọa độ Oxy, lấy các điểm O(0; 0), A(1; -1), B(2; -4), C(3; -9) và A’(-1; -1), B’(-2; -4), C’(-3; -9) rồi lần lượt nối chúng theo đường cong parabol.

Ta có đồ thị hàm số y = -$x^2$.

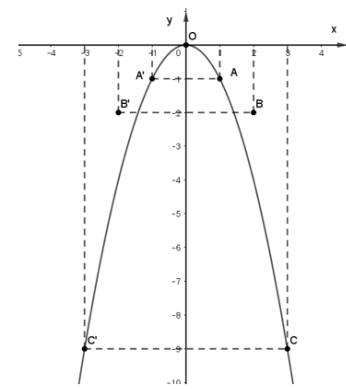
Bài 3: Vẽ parabol y² = 2px biết tiêu điểm của parabol là ^{$F\left(\frac{1}{4};0\right)$}

Lời giải:

Parabol có tiêu điểm $F\left(\frac{1}{4};0\right).$ $\Rightarrow \frac{p}{2}=\frac{1}{4}\Rightarrow p=\frac{1}{2}\Rightarrow$ (P): y² = x.

Bước 1. Lập bảng giá trị

Chú ý rằng ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau.

Bưóc 2. Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị.

Bước 3. Vẽ parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2.

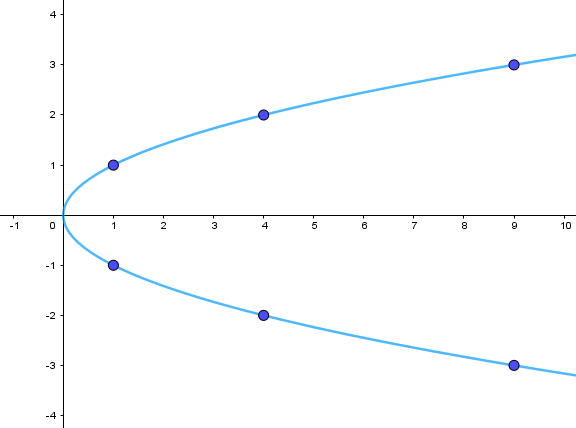
Bài tập tự luyện

Bài 1: Vẽ đồ thị Parabol:$y=2x^2-7x+10$. Và xét tính đồng biến, nghịch biến của nó trên tập xác định.

Bài 2: Vẽ đồ thị Parabol: - 3x² - 5x + 3. Và xét tính đồng biến, nghịch biến của nó trên tập xác định.

Bài 3: Lập bảng biến thiên và vẽ đồ thị các hàm số sau

a) y = x² - 3x + 2

b) y = -2x² + 4x

Bài 4: Cho hàm số y = -x² - 2x + 2

a) Lập bảng biến thiên và vẽ đồ thị các hàm số trên

b) Tìm m để đồ thị hàm số trên cắt đường thẳng y = m tại hai điểm phân biệt.

Xem thêm các dạng bài tập Toán liên quan hay và chi tiết khác:

Cách vẽ và bài tập parabol dễ hiểu nhất (2024)

Các công thức xác định toạ độ parabol hay nhất 2024

90 Bài tập hàm số. hàm số bậc hai và tam thức bậc hai (có đáp án năm 2024)

20 Bài tập Ứng dụng của hàm số bậc hai chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất (2024) cực hay, có đáp án

40 Bài tập Phương trình quy về phương trình bậc nhất, bậc hai (2024) cực hay, có đáp án