Các công thức xác định toạ độ parabol hay nhất 2024

Phương pháp giải tọa độ đỉnh của parabol, tọa độ giao điểm của parabol với các trục tọa độ 

Lí thuyết tổng hợp

- Khái niệm đường parabol: Một đường parabol là một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).

- Phương trình Parabol có dạng: $y=a{x}^2+bx+c$

- Gọi I là đỉnh của Parabol ta có $x_I=\frac{-b}{2a}$; $y_I=\frac{-\Delta }{4a}$ ( trong đó $\Delta =b^2-4ac$)

- Phương trình hoành độ giao điểm của hai đồ thị hàm số y = f(x) và y = g(x) là:

f(x) = g(x).

- Gốc tọa độ có tọa độ là O(0; 0)

- Trục tung có phương trình: x = 0.

- Trục hoành có phương trình: y = 0

Các công thức

Cho parabol (P): $y=a{x}^2+bx+c$, ta có:

- Tọa độ đỉnh I của Parabol là I$\left(\frac{-b}{2a};\frac{-\Delta }{4a}\right)$  (trong đó $\Delta =b^2-4ac$)

- Tọa độ giao điểm A của Parabol $y=a{x}^2+bx+c$ với trục tung x = 0:

Thay x = 0 vào phương trình Parabol có:$y=c\Rightarrow$ A (0; c)

- Tọa độ giao điểm B của Parabol $y=a{x}^2+bx+c$ với trục hoành y = 0:

Hoành độ của B là nghiệm của phương trình $y=a{x}^2+bx+c$ (1)

Nếu phương trình (1) vô nghiệm $\Rightarrow$ không tồn tại điểm B

Nếu phương trình (1) có nghiệm kép $\Rightarrow$ Parabol tiếp xúc với trục hoành tại B$\left(\frac{-b}{2a};0\right)$

Nếu phương trình (1) có hai nghiệm phân biệt  Parabol cắt trục hoành tại hai điểm $B_1\left(\frac{-b+\sqrt{\Delta }}{2a};0\right)$ và $B_2\left(\frac{-b-\sqrt{\Delta }}{2a};0\right)$

Bài tập vận dụng(có đáp án)

Bài 1: Cho Parabol có phương trình $y=-2x^2+4x-3$. Tìm giao điểm của Parabol với trục tung và trục hoành.

Lời giải:

Gọi M là giao điểm của Parabol với trục tung.

Vì M cũng thuộc trung tung nên ta có $M(0;y_M)$

Thay x = 0 vào $y=-2x^2+4x-3$ ta có: y = -2.0 + 4.0 – 3 = -3 

$\Rightarrow$ M (0; -3)

Gọi N là giao điểm của Parabol với trục hoành.

Vì N cũng thuộc trục hoành nên ta có: $N(x_N;0)$

Ta có phương trình hoành độ giao điểm của Parabol với trục hoành:

$-2x^2+4x-3=0$(1)

$\Delta =4^2-4.(-2).(-3)=-8<0$

$\Rightarrow$Phương trình (1) vô nghiệm. $\Rightarrow$ Parabol và trục hoành không có giao điểm.

Bài 2: Cho parabol có phương trình $y=x^2-3x+2$. Xác định tọa độ đỉnh của Parabol.

Lời giải:

Gọi I là đỉnh của Parabol $y=x^2-3x+2$. Ta có:

$$\begin{gathered} x_I=\frac{-b}{2a}=\frac{-(-3)}{2.1}=\frac{3}{2} \\ \Delta ={(-3)}^2-\mathrm{4.1.2}=1 \\ {y}_I=\frac{-\Delta }{4a}=\frac{-1}{4.1}=\frac{-1}{4} \\ \Rightarrow I\left(\frac{3}{2};\frac{-1}{4}\right) \end{gathered}$$

Vậy đỉnh của parabol là $I\left(\frac{3}{2};\frac{-1}{4}\right)$.

Bài 3: Tìm giao điểm của các Parabol sau với trục hoành.

a) $y=2x^2+3x-5$

b) $y=x^2-2x+1$

Lời giải:

a) $y=2x^2+3x-5$

Gọi M là giao điểm của Parabol với trục hoành.

Ta có phương trình hoành độ giao điểm của Parabol với trục hoành:

$y=2x^2+3x-5$ (1)

$\Delta ={(-3)}^2-\mathrm{4.2.}(-5)=49$> 0

$\Rightarrow$Phương trình (1) có hai nghiệm phân biệt.

$$\begin{gathered} x_1=\frac{-3+\sqrt{49}}{2.2}=1; \\ {x}_2=\frac{-3-\sqrt{49}}{2.2}=\frac{-5}{2} \end{gathered}$$

$\Rightarrow M_1\left(1;0\right)$ và $M_2\left(\frac{-5}{2};0\right)$

Vậy Parabol giao với trục hoành tại hai điểm $M_1\left(1;0\right)$ và $M_2\left(\frac{-5}{2};0\right)$.

b) $y=x^2-2x+1$

Gọi B là giao điểm của Parabol với trục hoành.

Ta có phương trình hoành độ giao điểm của Parabol với trục hoành:

$x^2-2x+1=0$(1)

$\Delta ={(-2)}^2-\mathrm{4.1.1}=0$

$\Rightarrow$Phương trình (1) có nghiệm kép $x=\frac{-(-2)}{2.1}=1$

$\Rightarrow$B(1; 0)

Vậy Parabol tiếp xúc với trục hoành tại điểm B(1; 0).

Bài 4. Xác định tọa độ đỉnh của parabol y = (-x² / 2) + 6x + 1 .

Lời giải:

Hoành độ đỉnh là x = (-b)/2a = 6;

Tung độ đỉnh là y = (-Δ)/4a = 19

$\to$Tọa độ đỉnh là (6;19).

Bài 5: Cho hàm số  $\left(P\right):y=-x^2+2x-3$. Hãy xác định tọa đỉnh của parabol (P)?

Lời giải:

Ta có các hệ số $a=-1,b=2,c=-3$.

$\Rightarrow -\frac{b}{2a}=-\frac{2}{2.\left(-1\right)}=1$ và $-\frac{\mathrm{\Delta }}{4a}=-2$.

Vậy đỉnh của parabol là $I\left(1;-2\right)$.

Bài 6: Cho parabol ${\displaystyle \left(P\right)}$ : ${\displaystyle y=x^2+5x-6}$. Xác định trục đối xứng, tọa độ đỉnh của parabol (P), tọa độ giao điểm của parabol (P) với trục hoành.

Lời giải:

- Trục đối xứng của ${\displaystyle \left(P\right)}$ :

${\displaystyle x=}$${\displaystyle -}$${\displaystyle \frac{b}{2a}}$ ${\displaystyle =}$ ${\displaystyle -}$${\displaystyle \frac{5}{2}}$  

- Tọa độ đỉnh của ${\displaystyle \left(P\right)}$ : ${\displaystyle (}$${\displaystyle -}$${\displaystyle \frac{b}{2a}}$ ${\displaystyle ;}$${\displaystyle -}$${\displaystyle \frac{\mathrm{\Delta }}{4a}}$${\displaystyle )}$

  ${\displaystyle \to }$ Tọa độ đỉnh là : ${\displaystyle (}$${\displaystyle -}$${\displaystyle \frac{5}{2}}$ ${\displaystyle ;}$${\displaystyle -}$${\displaystyle \frac{49}{4}}$${\displaystyle )}$

- Tọa độ giao điểm của ${\displaystyle \left(P\right)}$ trên trục hoành : 

${\displaystyle \Rightarrow }$ ${\displaystyle x^2+5x-6=0}$ ${\displaystyle \iff }$ $[\begin{array}{c}x=1\\ x=-6\end{array}$

Tọa độ giao điểm với ${\displaystyle Ox}$ : ${\displaystyle (1;0)}$  ${\displaystyle ,}$ ${\displaystyle (-6;0)}$

Bài 7: Xác định a, b, c biết parabol y = ax2 + bx + c Có đỉnh I(1 ; 4) và đi qua điểm D(3 ; 0)

Lời giải:

(P) : y = ax2 + bx + c

Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.

Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.

Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.

Giải hệ phương trình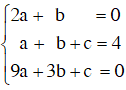  

ta được : a = –1 ; b = 2 ; c = 3.

Vậy a = –1 ; b = 2 ; c = 3.

Bài 8: Cho parabol  (P) y = 2x² + 4x - 3. Tọa độ đỉnh của parabol là:

Lời giải:

- Tọa độ đỉnh của I của (P) là:  $\left(-\frac{b}{2a};-\frac{∆}{4a}\right)$

$\to$Tọa độ đỉnh của parabol  là: I (-1:-5)

Bài tập tự luyện

Bài 1: Cho parabol có phương trình $y=2x^2-5x+6$. Xác định tọa độ đỉnh của Parabol.

Bài 2: Cho parabol có phương trình $y=x^2-3x+4$. Xác định tọa độ giao điểm của Parabol với trục tung và trục hoành.

Xem thêm các dạng bài tập toán hay khác:

Cách vẽ và bài tập parabol dễ hiểu nhất (2024)

250 Bài tập hàm số bậc hai (có đáp án năm 2023) - Toán 10

90 Bài tập hàm số. hàm số bậc hai và tam thức bậc hai (có đáp án năm 2023)

300 Bài tập dấu của tam thức bậc hai (có đáp án năm 2023)

200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)