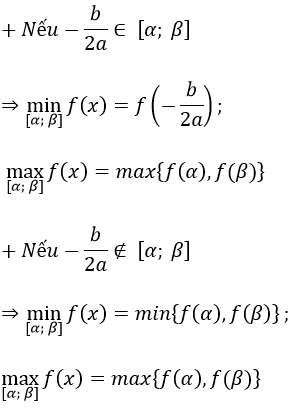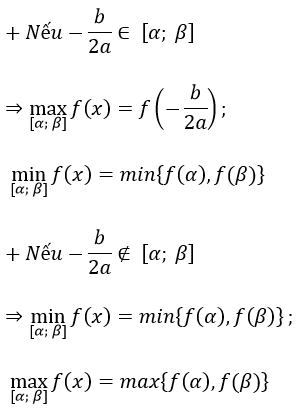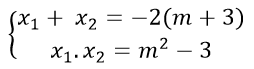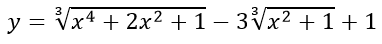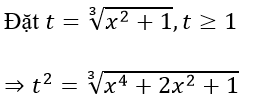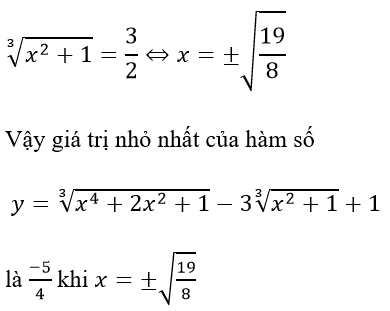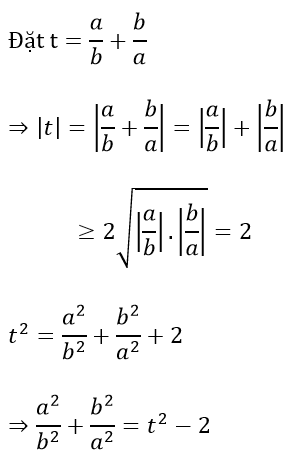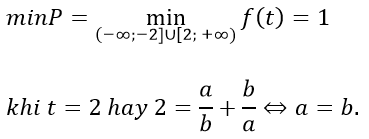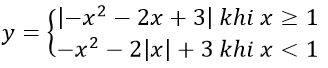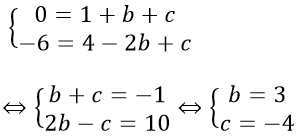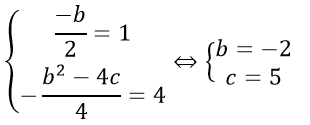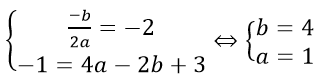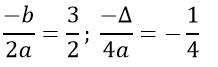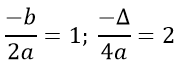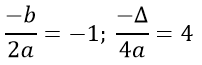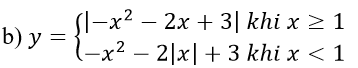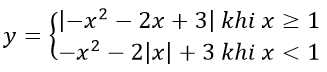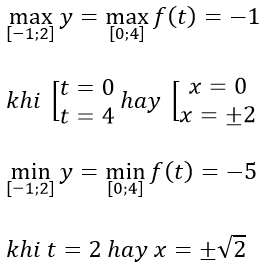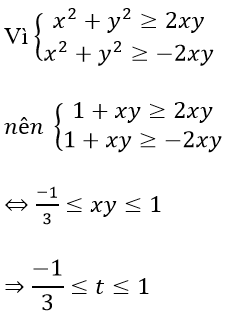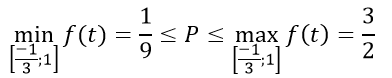20 Bài tập Ứng dụng của hàm số bậc hai chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất (2024) cực hay, có đáp án

Ứng dụng của hàm số bậc hai chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất

1. Phương pháp giải

Dựa vào đồ thị (bảng biến thiên) của hàm số y = ax² + bx + c, a ≠ 0 ta thấy nó đạt giá trị lớn nhất, nhỏ nhất trên [α; β] tại điểm x = α hoặc x = β hoặc x = -b/(2a). Cụ thể:

TH 1: a > 0

TH 2: a < 0:

2. Ví dụ minh họa

Ví dụ 1: Cho phương trình x² + 2(m + 3)x + m² - 3 = 0, m là tham số.

Tìm m để phương trình có hai nghiệm x₁; x₂ và P = 5(x₁ + x₂ ) - 2x₁x₂ đạt giá trị lớn nhất.

Hướng dẫn:

Ta có Δ' = (m + 3)² - (m² - 3) = 6m + 12

Phương trình có nghiệm ⇔ Δ' ≥ 0 ⇔ 6m + 12 ≥ 0 ⇔ m ≥ -2

Theo định lý Viét ta có:

P = 5(x₁ + x₂) - 2x₁x₂ = -10(m + 3) - 2(m² - 3) = -2m² - 10m - 24.

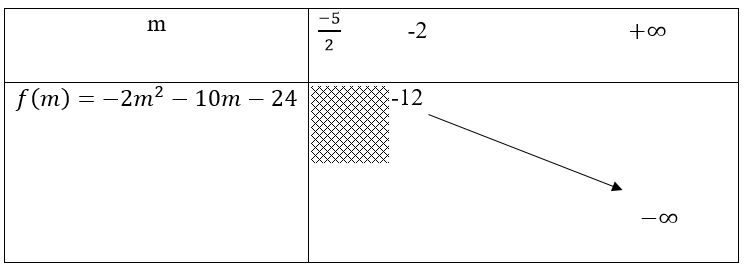
Xét hàm số f(m) = -2m² - 10m - 24 với m ∈ [-2; +∞)

Bảng biến thiên

Suy ra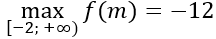khi và chỉ khi m = -2

Vậy m = -2 là giá trị cần tìm.

Ví dụ 2: Tìm giá trị nhỏ nhất của hàm số:

Hướng dẫn:

Khi đó hàm số trở thành y = t² - 3t + 1 với t ≥ 1

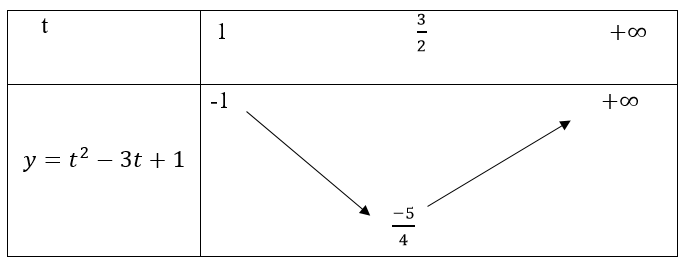
Bảng biến thiên

Suy ra giá trị nhỏ nhất của hàm số y = t² - 3t + 1 là (-5)/4 khi và chỉ khi t = 3/2 hay

Ví dụ 3: Cho các số thực a, b thoả mãn ab ≠ 0 . Tìm giá trị nhỏ nhất của biểu thức

Hướng dẫn:

Ta có P = t² - 2 - t + 1 = t² - t - 1

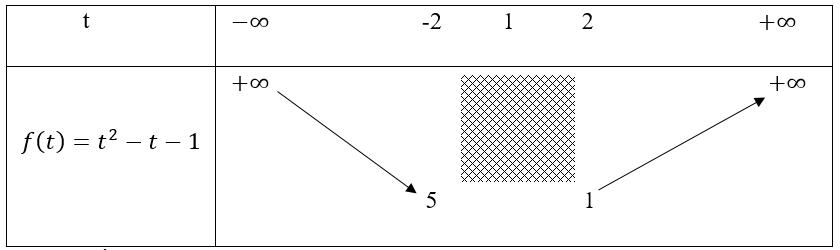
Xét hàm số f(t) = t² - t - 1 với t ∈ (-∞;-2] ∪ [2; +∞)

Bảng biến thiên

Từ bảng biến thiên ta có:

3. Bài tập tổng hợp (có đáp án)

Bài 1: Xác định phương trình của Parabol (P): y = x² + bx + c (P) trong các trường hợp sau:

a) (P) đi qua điểm A(1;0) và B (-2; -6)

b) (P) có đỉnh I(1; 4)

c) (P) cắt trục tung tại điểm có tung độ bằng 3 và có đỉnh S(-2; -1).

Bài 2: Lập bảng biến thiên và vẽ đồ thị các hàm số sau

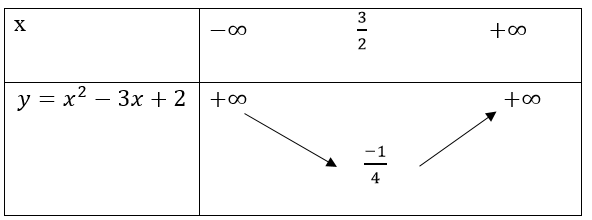
a) y = x² - 3x + 2

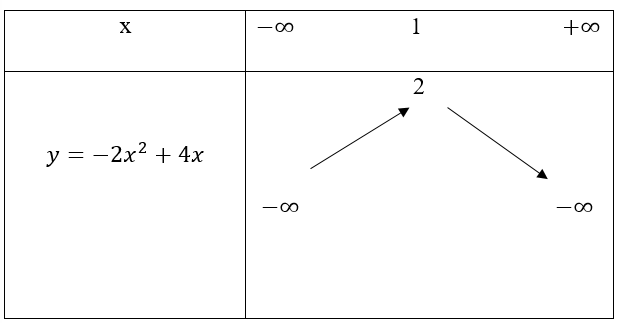
b) y = -2x² + 4x

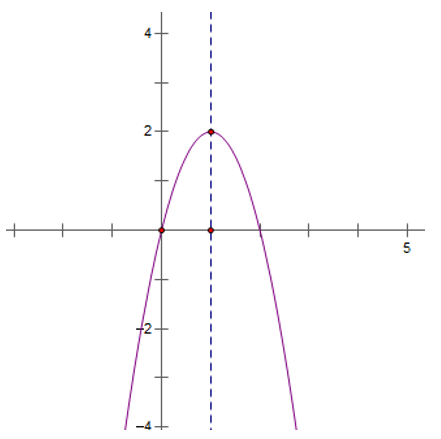
Bài 3: Cho hàm số y = -x² - 2x + 2

a) Lập bảng biến thiên và vẽ đồ thị các hàm số trên

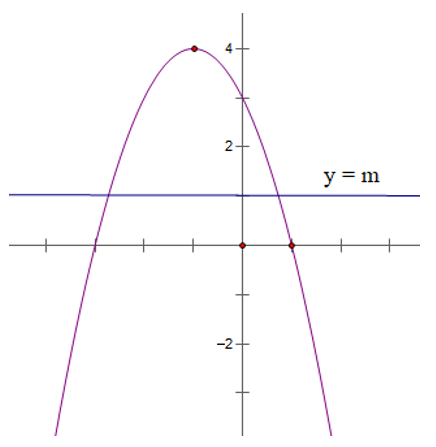
b) Tìm m để đồ thị hàm số trên cắt đường thẳng y = m tại hai điểm phân biệt

c) Sử dụng đồ thị, hãy nêu các khoảng trên đó hàm số chỉ nhận giá trị âm

d) Sử dụng đồ thị, hãy tìm giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên [-3; 1]

Bài 4: Vẽ đồ thị của hàm số sau:

a) y = -x² - 2|x| + 3

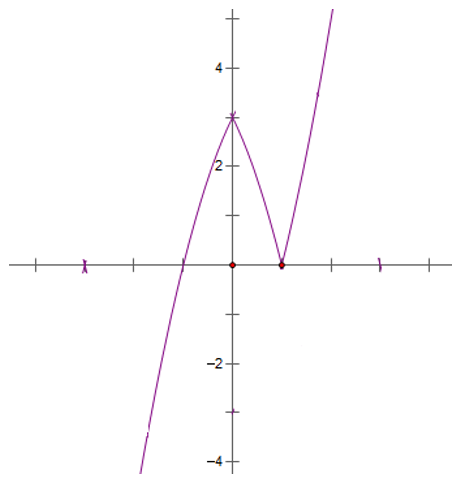
b)

Bài 5: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = x⁴ - 4x² - 1 trên [-1; 2]

Bài 6: Cho các số x, y thoả mãn: x² + y² = 1 + xy. Chứng minh rằng

            1/9 ≤ x⁴ + y⁴ - x²y² ≤ 3/2

Đáp án và hướng dẫn giải

Bài 1:

a) Vì (P) đi qua A, B nên

Vậy (P): y = x² + 3x - 4 .

b) Vì (P) có đỉnh I(1; 4) nên:

Vậy (P): y = x² - 2x + 5.

c) (P) cắt Oy tại điểm có tung độ bằng 3 suy ra c = 3

(P) có đỉnh S (-2; -1) suy ra:

Vậy (P): y = x² + 4x + 3.

Bài 2.

a) Ta có:

Bảng biến thiên

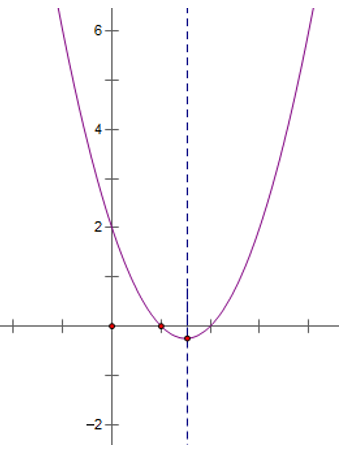
Suy ra đồ thị hàm số y = x² - 3x + 2 có đỉnh là I(3/2; -1/4), đi qua các điểm A(2; 0); B (1; 0), C(0; 2).

Đồ thị hàm số nhận đường thẳng x = 3/2 làm trục đối xứng và hướng bề lõm lên trên.

b) Ta có

Bảng biến thiên

Suy ra đồ thị hàm số y = -2x² + 4x có đỉnh là I(1; 2), đi qua các điểm O(0; 0), B (2; 0).

Đồ thị hàm số nhận đường thẳng x = 1 làm trục đối xứng và hướng bề lõm xuống dưới.

Bài 3:

a) Ta có:

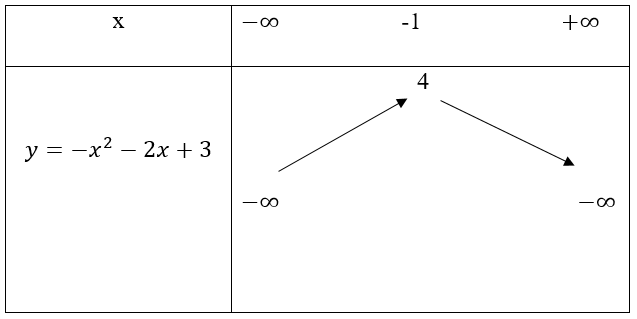
Bảng biến thiên

Suy ra đồ thị hàm số y = -x² - 2x + 3 có đỉnh là I(-1; 4), đi qua các điểm A(1; 0), B (-3; 0).

Đồ thị hàm số nhận đường thẳng x = -1 làm trục đối xứng và hướng bề lõm xuống dưới.

b) Đường thẳng y = m song song hoặc trùng với trục hoành do đó dựa vào đồ thị ta có

Với m < 4 đường thẳng y = m và parabol y = -x² - 2x + 3 cắt nhau tại hai điểm phân biệt.

c) Hàm số nhận giá trị dương ứng với phần đồ thị nằm hoàn toàn trên trục hoành

Do đó hàm số chỉ nhận giá trị âm khi và chỉ khi x ∈ (-∞; -2) ∪ (1; +∞).

d) Dựa vào bảng biến thiên, ta có:

Bài 4: a) y = -x² - 2|x| + 3

a) Vẽ đồ thị hàm số (P): y = -x² - 2x + 3 có đỉnh I (-1; - 4), trục đối xứng x = -1, đi qua các điểm A(1; 0), B (-3; 0). Bề lõm hướng xuống dưới.

Khi đó (P₁ ) là đồ thị hàm số y = -x² - 2|x| + 3 là gồm phần bên phải trục tung của (P) và phần lấy đối xứng của nó qua trục tung.

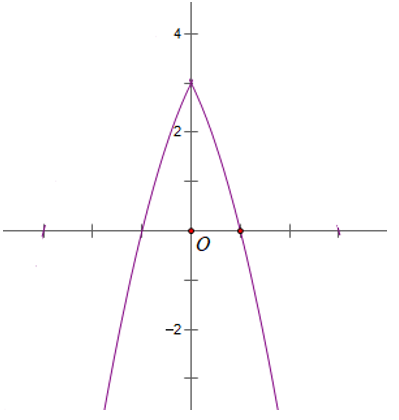
b) Gọi (P₂ ) là phần đồ thị của (P) nằm trên trục hoành và lấy đối xứng của phần nằm dưới trục hoành qua trục Ox.

Vậy đồ thị hàm số

gồm phần bên đồ thị bên phải đường thẳng x = 1 của (P₂ ) và phần đồ thị bên trái đường thẳng x = 1 của (P₁ ).

Bài 5:

Đặt t = x². Với x ∈ [-1; 2] ta có t ∈ [0; 4]

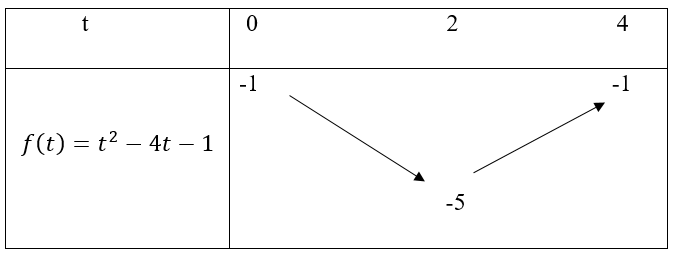
Hàm số trở thành f(t) = t² - 4t - 1 với t ∈ [0; 4].

Bảng biến thiên

Suy ra :

Bài 6:

Đặt P = x⁴ + y⁴ - x²y²

Ta có P = (x² + y²)² - 3x²y² = (1+xy)² - 3x²y² = -2x²y² + 2xy + 1

Đặt t = xy, khi đó P = -2t² + 2t + 1

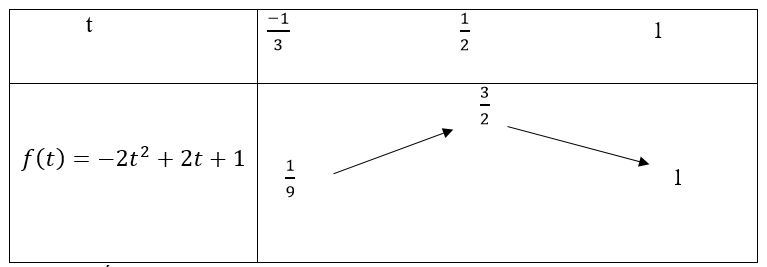
Xét hàm số f(t) = -2t² + 2t + 1 trên [(-1)/3; 1]

Ta có bảng biến thiên

Từ bảng biến thiên ta có :

Suy ra điều phải chứng minh.

Xem thêm các dạng bài tập liên quan khác:

150 Bài tập hàm số (có đáp án năm 2024)

250 Bài tập hàm số bậc hai (có đáp án năm 2024)

100 Bài tập về Phương trình quy về phương trình bậc hai (có đáp án năm 2024)

90 Bài tập hàm số. hàm số bậc hai và tam thức bậc hai (có đáp án năm 2024) - Toán 10

Cách vẽ đồ thị hàm số bậc 2 chi tiết nhất và bài tập (2024)