50 Bài tập về trường hợp đồng dạng thứ hai trong tam giác (có đáp án năm 2024) - Toán 8

Bài giảng Toán 8 Bài 6: Trường hợp đồng dạng thứ hai

Kiến thức cần nhớ

1. Định lí

- Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng

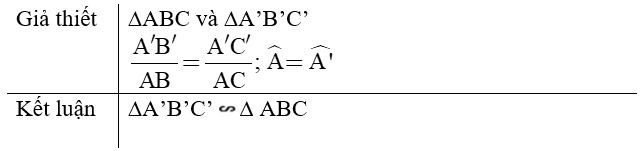
- Ví dụ 1. Cho tam giác ABC có AB = 15cm; AC = 20cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm; AE = 6cm.

Chứng minh ∆AED$\infty$∆ ABC.

Lời giải:

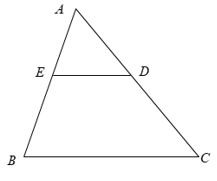
Xét ∆AED và ∆ABC có:

$\left\{\begin{array}{l}\hat{\mathrm{A}} \mathrm{chung}\\ \frac{\mathrm{AE}}{\mathrm{AB}}=\frac{\mathrm{AD}}{\mathrm{AC}}\left(\frac{6}{15}=\frac{8}{20}=\frac{2}{5}\right)\end{array}\right.$

Suy ra: ∆AED$\infty$∆ ABC (c – g – c).

Các dạng bài tập về trường hợp đồng dạng thứ hai trong tam giác

(Xem chi tiết trong file đính kèm)

Dạng 1: Chứng minh hai tam giác đồng dạng

Phương pháp:

- Xét hai tam giác, chọn ra hai góc bằng nhau và chứng minh (nếu cần).

- Lập tỉ số hai cạnh tạo nên mỗi góc đó, rồi chứng minh chúng bằng nhau.

- Kết luận hai tam giác đồng dạng.

Dạng 2: Sử dụng trường hợp đồng dạng thứ hai để tính độ dài cạnh hoặc chứng minh các góc bằng nhau

Phương pháp giải:

Sử dụng trường hợp đồng dạng thứ hai (nếu cần) để chứng minh hai tam giác đồng dạng, từ đó suy ra các cặp góc tương ứng bằng nhau hoặc cặp cạnh tương ứng còn lại bằng nhau.

Bài tập (có hướng dẫn)

1. Bài tập vận dụng

Bài 1. Cho góc $\widehat{\mathrm{xOy}}\ne 180°$. Trên tia Ox lấy 2 điểm A và C sao cho OA = 4cm; OC = 10cm. Trên tia Oy lấy hai điểm B và D sao cho OB = 5cm; OD = 8cm

Chứng minh ∆OBC$\infty$∆OAD.

Lời giải:

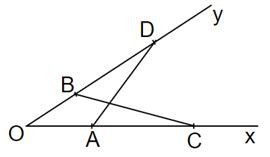
Xét ∆OBC và ∆ OAD có:

$\hat{\mathrm{O}}$ chung.

$\frac{\mathrm{OB}}{\mathrm{OA}}=\frac{\mathrm{OC}}{\mathrm{OD}}\left(\frac{5}{4}=\frac{10}{8}\right)$

Suy ra: ∆OBC ∆ OAD (c – g – c) (đpcm).

Bài 2. Cho tam giác ABC có AC = 12cm; BC = 8cm. Trên cạnh  AC lấy điểm E sao cho AE = 7cm. Trên cạnh BC lấy điểm D sao cho DC = 4,5. Chứng minh; $\widehat{\mathrm{EDC}}=\widehat{\mathrm{BAC}}$.

Lời giải:

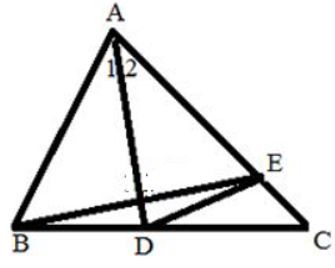
Ta có: CE = AC – AE = 10 – 7 = 3cm

Xét ∆CED và ∆ CBA có: 

$\hat{\mathrm{C}}$ chung.

$\frac{\mathrm{CE}}{\mathrm{CB}}=\frac{\mathrm{CD}}{\mathrm{CA}}\left(\frac{3}{8}=\frac{4,5}{12}\right)$

Suy ra: ∆CED$\infty$∆CBA (c.g.c)

Do đó: $\widehat{\mathrm{EDC}}=\widehat{\mathrm{BAC}}$(2 góc tương ứng) (đpcm).

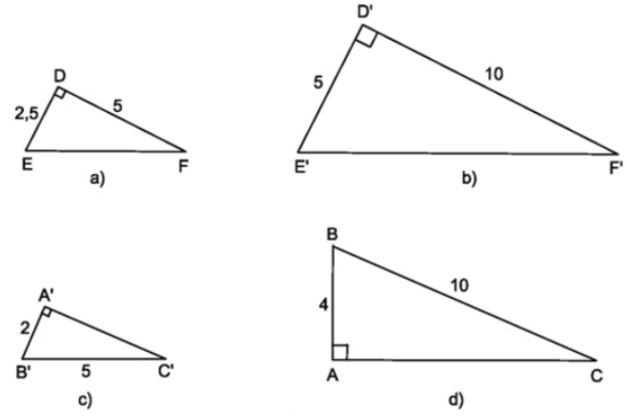
Bài 3. Chỉ ra các tam giác đồng dạng với nhau trong hình vẽ sau?

Lời giải:

+ Xét ∆DEF và ∆ D’E’F’ có:

$$\begin{gathered} \hat{\mathrm{D}}=\widehat{\mathrm{D}\text{'}}=90° \\ \frac{\mathrm{DE}}{\mathrm{D}\text{'}\mathrm{E}\text{'}}=\frac{\mathrm{DF}}{\mathrm{D}\text{'}\mathrm{F}\text{'}}=\frac{1}{2} \end{gathered}$$

Suy ra: ∆DEF$\infty$∆D’E’F’.

+ Áp dụng định lí py tago ta có:

$$\begin{gathered} \mathrm{A}\text{'}\mathrm{C}\text{'}=\sqrt{\mathrm{B}\text{'}\mathrm{C}{\text{'}}^2-\mathrm{A}\text{'}\mathrm{B}{\text{'}}^2}=\sqrt{21} \\ \mathrm{AC}=\sqrt{{\mathrm{BC}}^2-{\mathrm{AB}}^2}=\sqrt{84}=2\sqrt{21} \end{gathered}$$

Xét ∆ABC và ∆ A’B’C’ có:

$$\begin{gathered} \hat{\mathrm{A}}=\widehat{\mathrm{A}\text{'}}=90° \\ \frac{\mathrm{AB}}{\mathrm{A}\text{'}\mathrm{B}\text{'}}=\frac{\mathrm{AC}}{\mathrm{A}\text{'}\mathrm{C}\text{'}}=2 \end{gathered}$$

Suy ra: ∆ABC$\infty$∆A’B’C’.

Bài 3: Cho hình vẽ dưới, với: OA = 5cm, OB = 16cm, OC = 8cm, OD = 10cm.

Chứng minh tam giác OCB đồng dạng với tam giác OAD.

Bài giải:

Xét hai tam giác OCB và ODA, ta có:

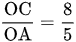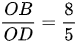;  suy ra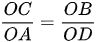 

góc O chung

Vậy tam giác OCB đồng dạng với tam giác OAD (c.g.c)

Bài 4: Cho tam giác ABC có . Điểm D thuộc cạnh BC sao cho  Tính độ dài AD.

Bài giải:

Xét hai tam giác ACB và DCA, ta có:

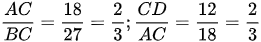
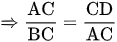
Góc C chung suy ra tam giác ACB đồng dạng với tam giác DCA (c.g.c)

.

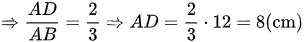Bài 5:  Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD = 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm. Chứng minh rằng:

a) Tam giác AED đồng dạng với tam giác ABC.

b) .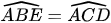

Bài giải:

a) Xét hai tam giác AED và ABC:

AE = 3cm; AD = 6cm.

Ta có .

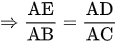 và góc A chung.

Vậy tam giác AED đồng dạng với tam giác ABC (c.g.c)

b) Xét hai tam giác ABE và ACD:

Ta có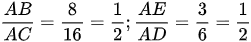 

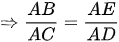 và góc A chung. Vậy tam giác ABE đồng dạng với tam giác ACD (c.g.c)

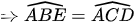 (hai góc tương ứng)

2. Bài tập tự luyện

(Xem trong file đính kèm)

Xem thêm các dạng bài tập liên quan khác:

60 Bài tập về trường hợp đồng dạng thứ nhất trong tam giác (có đáp án năm 2023)

60 Bài tập về trường hợp đồng dạng thứ ba trong tam giác (có đáp án năm 2023)

60 Bài tập về các trường hợp đồng dạng của tam giác vuông (có đáp án năm 2023)

300 Bài tập Toán 8 chương 3: Tam giác đồng dạng (có đáp án năm 2023)

60 Bài tập về Tính chất đường phân giác của tam giác (có đáp án năm 2023)