Bài giảng Toán 8 Bài 7: Trường hợp đồng dạng thứ ba
Kiến thức cần nhớ
1. Định lí
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Ví dụ 1. Cho tam giác ABC và các đường cao BH, CK. Chứng minh ∆ABH ∆ ACK.
Lời giải:
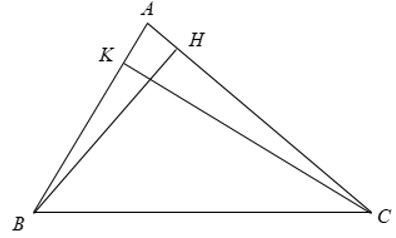
Xét ∆ABH và ∆ACK có:
Suy ra: ∆ABH ∆ACK.
Các dạng bài toán về trường hợp đồng dạng thứ ba trong tam giác
(Xem chi tiết trong file đính kèm)
Dạng 1. Chứng minh hai tam giác đồng dạng.
Phương pháp giải:
Chỉ ra hai cặp góc tương ứng bằng nhau trong hai tam giác để suy ra hai tam giác đồng dạng.
Dạng 2. Sử dụng các trường hợp đồng dạng thứ ba để tính độ dài các cạnh, chứng minh hệ thức cạnh hoặc chứng minh các góc bằng nhau.
Phương pháp giải:
Sử dụng trường hợp đồng dạng thứ ba (nếu cần) để chứng minh hai tam giác đồng dạng, từ đó suy ra các cặp góc tương ứng bằng nhau hoặc cặp cạnh tương ứng tỉ lệ.
Bài tập (có hướng dẫn)
1. Bài tập vận dụng
Bài 1. Cho hình bên, ABCD là hình thang (AB// CD) có AB = 12 cm; CD = 27cm . Tính độ dài đoạn BD gần nhất bằng bao nhiêu?
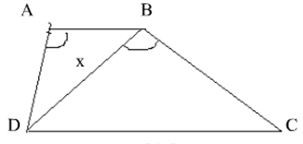
Lời giải:
Xét ∆ABD và ∆BDC có:
Suy ra: ∆ABD ∆BDC (g.g).
hay
Vậy BD = 18cm.
Bài 2. Cho góc xOy khác góc bẹt. Trên tia Ox lấy 2 điểm A và B sao cho: OA = 5cm; OB = 16cm. Trên tia Oy, lấy hai điểm C và D sao cho OC = 8cm; OD =10cm.
a) Chứng minh ∆OCB ∆OAD.
b) Gọi I là giao điểm của các cạnh AD và BC. Chứng minh rằng ∆IBA ∆ IDC
Lời giải:
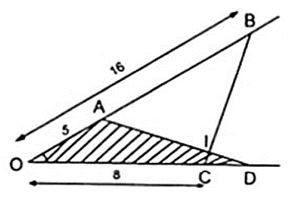
a) Xét ∆OCB và ∆ OAD có
Suy ra: ∆OCB ∆OAD (c.g.c)
b) Theo a ta có: ∆OCB ∆OAD
hay (1)
Mà (vì đối đỉnh) (2)
Từ (1) và (2) suy ra: ∆IBA ∆IDC (g.g)
Bài 3. Tìm x, y trong hình vẽ sau:
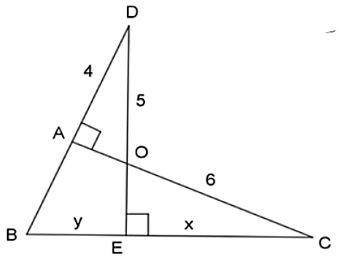
Lời giải:
Xét ∆OAD và ∆OEC có:
(hai góc đối đỉnh).
Suy ra: ∆OAD ∆OEC (g.g)
Áp dụng định lý py ta go vào tam giác ADO có:
AO2 = OD2 – DA2 = 9 nên AO = 3.
Khi đó; AC = AO + OC = 3 + 6 = 9
Xét ∆OAD và ∆BAC có:
(cùng phụ với góc ).
Suy ra: ∆OAD ∆BAC (g.g)
Suy ra:
Bài 4. Cho tam giác ABC cân tại A và 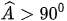 . Lấy điểm M nằm giữa hai điểm B và C. Trên nửa mặt phẳng chứa C bờ là AB, vẽ tia Bx sao cho
. Lấy điểm M nằm giữa hai điểm B và C. Trên nửa mặt phẳng chứa C bờ là AB, vẽ tia Bx sao cho  . Tia Bx cắt AM tại D.
. Tia Bx cắt AM tại D.
a) Chứng minh 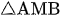 và
và  đồng dạng.
đồng dạng.
b) Chứng minh 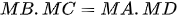 .
.
Bài giải:

a) Xét 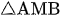 và
và  có:
có:
 (giả thiết)
(giả thiết)
 chung
chung
Do đó tam giác AMB đồng dạng với tam giác ABD (g.g)
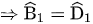 mà
mà 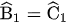 (giả thiết)
(giả thiết)

b) Xét  và
và  có
có 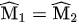 (đối đỉnh)
(đối đỉnh)
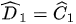 (chứng minh trên)
(chứng minh trên)
Do đó tam giác BMD đồng dạng với tam giác AMC (g.g)  .
.
Bài 5. Cho hình thang ABCD  và O là giao điểm của hai đường chéo AC và BD.
và O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh 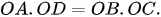
b) Đường thẳng qua O vuông góc với AB cắt AB và CD lần lượt tại H và K. Chứng minh  .
.
Bài giải:

Ta có 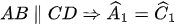 và
và 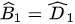 .
.
Do đó tam giác AOB đồng dạng với tam giác COD (g.g)
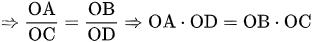 .
.
b) Dễ thấy tam giác AHO đồng dạng với tam giác CKO (g.g)  (1)
(1)
Tương tự tam giác BHO đồng dạng với tam giác DKO 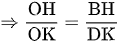 (2)
(2)
Từ (1) và (2)  .
.
 .
.
Bài 6. Cho hình vuông ABCD, trên các cạnh AB và BC lần lượt lấy các điểm P và Q sao cho BP = BQ. Gọi H là chân đường vuông góc kẻ từ B đến PC. Chứng minh rằng 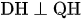 .
.
Bài giải:

Ta có 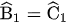 (cùng phụ với
(cùng phụ với 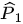 )
)
Do đó tam giác BHP đồng dạng với tam giác CHB (g.g)
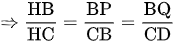 (1)
(1)
(vì BQ = BP và CB = CD)
Xét tam giác BHQ và tam giác CHD có:
 (cùng phụ với
(cùng phụ với  ) và (1). Do đó tam giác BHQ đồng dạng với tam giác CHD (g.g)
) và (1). Do đó tam giác BHQ đồng dạng với tam giác CHD (g.g)

Mà  (giải thiết)
(giải thiết)  hay
hay  .
.
Chứng tỏ 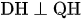 .
.
2. Bài tập tự luyện
(Xem trong file đính kèm)
Xem thêm các dạng bài tập liên quan khác:
50 Bài tập về trường hợp đồng dạng thứ hai trong tam giác (có đáp án năm 2024)
60 Bài tập về trường hợp đồng dạng thứ ba trong tam giác (có đáp án năm 2023)
60 Bài tập về các trường hợp đồng dạng của tam giác vuông (có đáp án năm 2023)
300 Bài tập Toán 8 chương 3: Tam giác đồng dạng (có đáp án năm 2023)
60 Bài tập về Tính chất đường phân giác của tam giác (có đáp án năm 2023)












