Bài giảng Toán 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông
Kiến thức cần nhớ
1. Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông
Hai tam giác vuông đồng dạng với nhau nếu:
+ Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
+ Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
2. Dấu hiệu đặc biệt nhận biết hai tam vuông đồng dạng
- Định lý 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
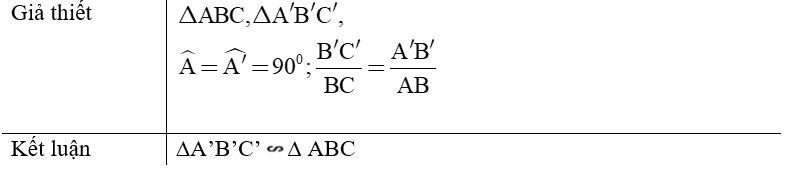
3. Tỉ số hai đường cao, tỉ số diện tích của hai tam giác đồng dạng
- Định lý 2: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
Cho hai tam giác ABC và A’B’C’ với tỉ số đồng dạng là , hai đường cao tương ứng là AH và A’H’.
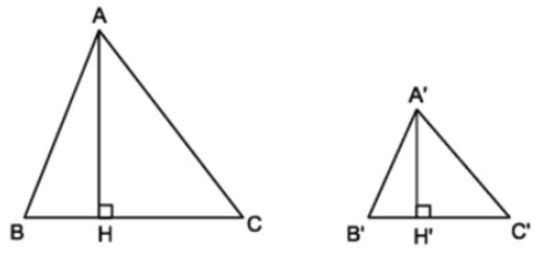
Khi đó, ta có tỉ số hai đường cao là: .
- Định lý 3: Tỉ số diện tích hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

Ví dụ 1. Cho tam giác ABC đồng dạng với tam giác MNP theo tỉ số . Biết đường cao xuất phát từ A của tam giác ABC là AH = 12cm. Tính đường cao xuất phát từ M của tam giác MNP?
Lời giải:
Gọi đường cao xuất phát từ M của tam giác MNP là MK.
Vì tam giác ABC đồng dạng với tam giác MNP theo tỉ số nên
Các dạng bài tập toán về trường hợp đồng dạng của tam giác vuông
(Xem chi tiết trong file đính kèm)
Dạng 1. Chứng minh hai tam giác vuông đồng dạng.
Phương pháp giải:
Có thể sử dụng một trong các cách sau:
+ Cách 1: Áp dụng trường hợp đồng dạng của hai tam giác thường vào tam giác vuông.
+ Cách 2: Sử dụng đặc biệt nhận biết hai tam giác vuông đồng dạng.
Dạng 2. Sử dụng trường hợp đồng dạng của tam giác vuông để giải toán.
Phương pháp giải:
Sử dụng các trường hợp đồng dạng của hai tam giác vuông (nếu cần) để chứng minh hai tam giác đồng dạng, từ đó suy ra các cặp góc tương ứng bằng nhau hoặc cặp cạnh tương ứng tỉ lệ, từ đo suy ra điều cần chứng minh.
Dạng 3. Tỉ số diện tích của hai tam giác.
Phương pháp giải:
Sử dụng định lý tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Bài tập (có hướng dẫn)
1. Bài tập vận dụng
Bài 1. Cho tam giác vuông ABC vuông tại A, lấy điểm D bất kì thuộc BC, một đường thẳng vuông góc với BC tại D cắt các đường thẳng AC và AB lần lượt tại E và F.
a) Chứng minh  .
.
b) Gọi AH là đường cao của  , biết HB = 3cm, HC = 12cm. Tính đường cao AH.
, biết HB = 3cm, HC = 12cm. Tính đường cao AH.
Lời giải:

a) Ta có 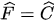 (cùng phụ với
(cùng phụ với 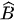 )
)
Do đó hai tam giác vuông BDF đồng dạng với tam giác EDC (g.g)
 .
.
b) Ta có  (cùng phụ với
(cùng phụ với 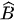 )
)
Do đó tam giác AHB đồng dạng với tam giác CHA (g.g)
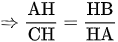
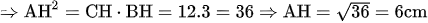 .
.
Bài 2. Kẻ đường cao BD và CE của tam giác ABC và các đường cao DF và EG của tam giác ADE.
a) Chứng minh 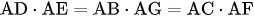 .
.
b) Chứng minh  .
.
Lời giải:

a) Xét 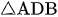 và
và 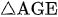 có
có  chung và
chung và 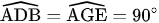 (giả thiết)
(giả thiết)
nên tam giác ADB đồng dạng với tam giác AGE (g.g)
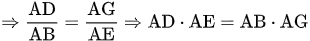 (1)
(1)
Tương tự tam giác ADF đồng dạng với tam giác ACE.
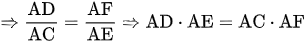 (2)
(2)
b) Từ (1) và (2) 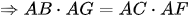
Theo định lí Ta lét đảo 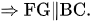
Bài 3.
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng H là giao điểm các đường phân giác trong 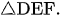
Lời giải:

Xét 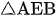 và
và 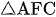 có
có  chung.
chung.
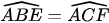 (cùng phụ với
(cùng phụ với  )
)
Suy ra tam giác AEB đồng dạng với tam giác AFC (g.g)  .
.
Xét tam giác AEF đồng dạng với tam giác ABC (c.g.c) 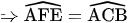 (1)
(1)
Lý luận tương tự như trên ta có: tam giác BFD đồng dạng với tam giác BCA (c.g.c)
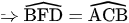 (2)
(2)
Từ (1) và (2) cho 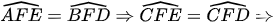 FC là tia phân giác của
FC là tia phân giác của  .
.
Tương tự:  là tia phân giác của
là tia phân giác của  .
.
Vậy H là giao điểm các đường phân giác trong tam giác ABC.
Bài 4. Cho tam giác ABC vuông tại A có chân đường cao AH chia cạnh huyền BC thành hai đoạn thẳng có độ dài lần lượt là HB = 16 cm và HC = 25 cm. Tính diện tích của tam giác ABC?
Lời giải:
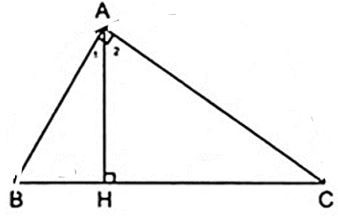
Xét tam giác AHB và tam giác CHA có:
(cùng phụ )
Suy ra: ∆AHB ∆CHA (g.g).
Hay
Ta có:
Bài 5. Cho tam giác ABC vuông tại A. Gọi H là hình chiếu vuông góc của A lên BC. Biết AB = 5cm; AC = 12cm.
a) Tính BH?
b) Chứng minh ∆AHB ∆CHA
Lời giải:
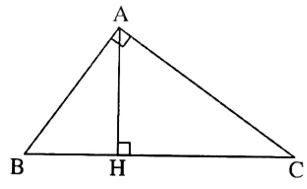
a) Áp dụng định lí Pyata go vào tam giác vuông ABC có:
BC2 = AB2 + AC2 = 25 + 144= 169 nên BC = 13cm
Xét ∆ABC và ∆ HBA có:
chung
Suy ra: ∆ABC ∆HBA (g.g)
b) Xét ∆AHB và ∆CHA có:
(cùng phụ với góc )
Suy ra: ∆AHB ∆CHA (g.g).
Bài 6. Cho tam giác ABC vuông tại A. Dựng hai đường phân giác trong BH; CN của góc B và góc C. Hai đường này cắt nhau tại I. Gọi K là hình chiếu vuông góc của I lên BC. Chứng minh:
a) ∆IKC ∆NAC
b) ∆IKB ∆HAB.
Lời giải:
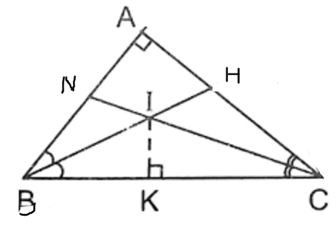
a) Xét ∆IKC và ∆NAC có:
(vì CN là tia phân giác của )
Suy ra: ∆IKC ∆NAC (g.g) ( đpcm)
b) Xét ∆IKB và ∆HAB có:
(vì BH là tia phân giác của )
Suy ra: ∆IKB ∆HAB (g.g) (đpcm)
2. Bài tập tự luyện
(Xem trong file đính kèm)
Xem thêm các dạng bài tập liên quan khác:
60 Bài tập về trường hợp đồng dạng thứ nhất trong tam giác (có đáp án năm 2023)
60 Bài tập về trường hợp đồng dạng thứ ba trong tam giác (có đáp án năm 2023)
50 Bài tập về trường hợp đồng dạng thứ hai trong tam giác (có đáp án năm 2024)
300 Bài tập Toán 8 chương 3: Tam giác đồng dạng (có đáp án năm 2023)
60 Bài tập về Tính chất đường phân giác của tam giác (có đáp án năm 2023)












