50 bài tập về những hằng đẳng thức đáng nhớ (có đáp án 2024) – Toán 8

Những hằng đẳng thức đáng nhớ lớp 8 và cách giải các dạng bài tập - Toán lớp 8

A. Bình phương của một tổng, bình phương của một hiệu và hiệu hai bình phương

I. Lý thuyết

1. Bình phương của một tổng:

${(A+B)}^2=A^2+2AB+B^2$

2. Bình phương của một hiệu:

${(A-B)}^2=A^2-2AB+B^2$

3. Hiệu hai bình phương

$A^2-B^2$ = (A – B)(A + B)

II. Các dạng bài

1. Dạng 1: Thực hiện phép tính

a. Phương pháp giải:

Sử dụng trực tiếp các hằng đẳng thức đã học để khai triển các biểu thức

b, Ví dụ minh họa:

VD1: Thực hiện phép tính:

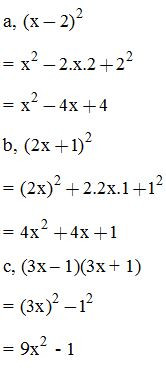
VD2: Viết các biểu thức sau dưới dạng bình phương một tổng hoặc bình phương một hiệu:

a, $4x^2+4x+1$

b, $x^2-8x+16$

Giải:

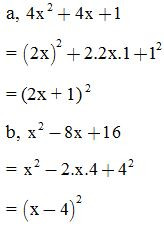
2. Dạng 2: Chứng minh các đẳng thức

a. Phương pháp giải:

Áp dụng linh hoạt các hằng đẳng thức, lựa chọn vế có thể dễ dàng áp dụng các hằng đẳng thức.

b. Ví dụ minh họa:

Chứng minh các đẳng thức sau:

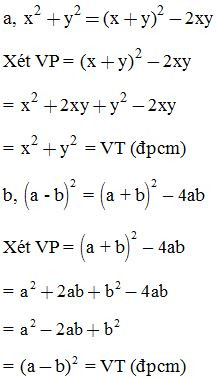
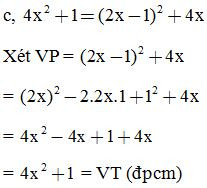
3. Dạng 3: Tính nhanh

a. Phương pháp giải:

Áp dụng linh hoạt các hằng đẳng thức cho các số tự nhiên

b. Ví dụ minh họa:

Tính nhanh:

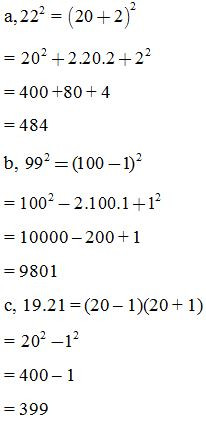
4. Dạng 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức

a. Phương pháp giải:

Sử dụng các hằng đẳng thức và cần chú ý:

$A^2\ge 0$ và $-A^2\le 0$

b. Ví dụ minh họa:

a, Chứng minh $9x^2-6x+3$ luôn dương với mọi x

Giải:

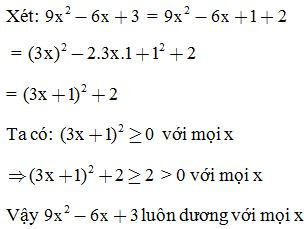
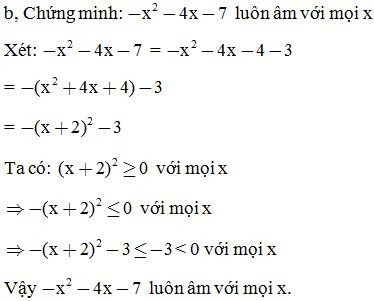
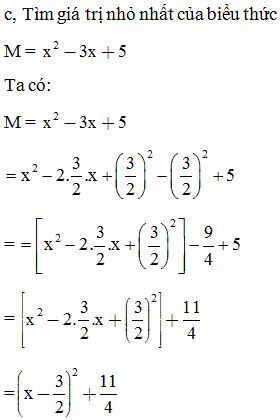
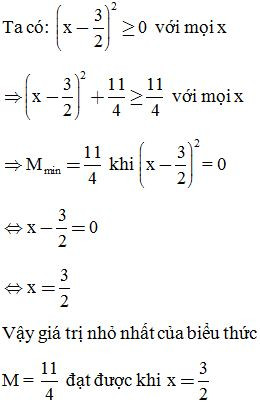
B. Lập phương của một tổng hoặc một hiệu

I. Lý thuyết

1. Lập phương của một tổng:

${\left(A+B\right)}^3$$=A^3+3A^{2}B+3A{B}^2+B^3$

2. Lập phương của một hiệu:

${\left(A-B\right)}^3=$$A^3-3A^{2}B+3A{B}^2-B^3$

II. Các dạng bài

1. Dạng 1: Sử dụng hằng đẳng thức để khai triển và rút gọn biểu thức và tính giá trị biểu thức:  

a. Phương pháp giải:

Sử dụng hằng đẳng thức đã học để khai triển và rút gọn biểu thức.

b. Ví dụ minh họa:

VD1: Thực hiện phép tính:

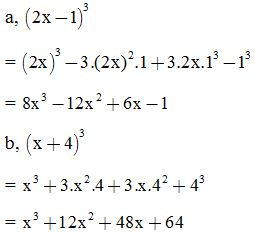
VD2: Rút gọn biểu thức:

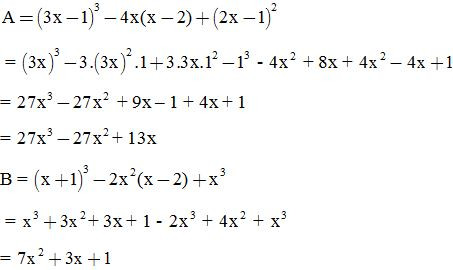
VD3: Viết các biểu thức sau dưới dạng lập phương một tổng hoặc lập phương một hiệu:

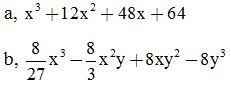
Giải:

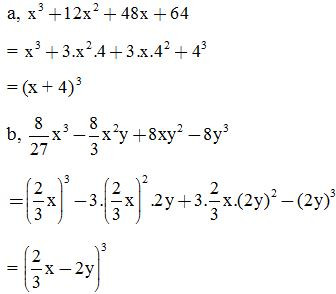
VD4: Tính giá trị các biểu thức sau:

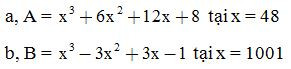
Giải:

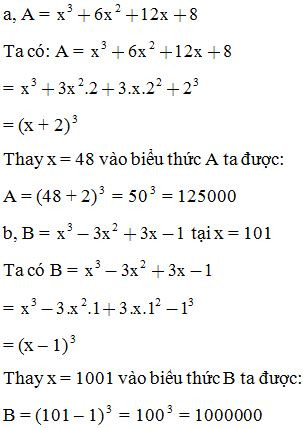
2. Dạng 2: Sử dụng hằng đẳng thức để tính nhanh:

a. Phương pháp giải:

Sử dụng linh hoạt các hằng đẳng thức để tính nhanh

b. Ví dụ minh họa:

Tính nhanh:

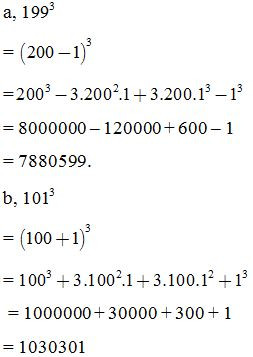
C. Tổng hoặc hiệu hai lập phương

I. Lý thuyết:

1. Tổng hai lập phương:

$A^3+B^3=$$(A+B)(A^2-AB+B^2)$

2. Hiệu hai lập phương:

$A^3-B^3=$$(A-B)(A^2+AB+B^2)$

II. Các dạng bài:

1. Dạng 1: Sử dụng hằng đẳng thức để rút gọn và khai triển biểu thức:

a. Phương pháp giải:

Sử dụng các hằng đẳng thức đã học để khai triển hoặc rút gọn biểu thức.

b. Ví dụ minh họa:

VD1: Thực hiện phép tính:

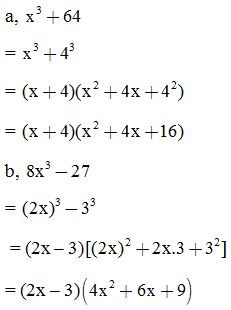
VD2: Rút gọn biểu thức:

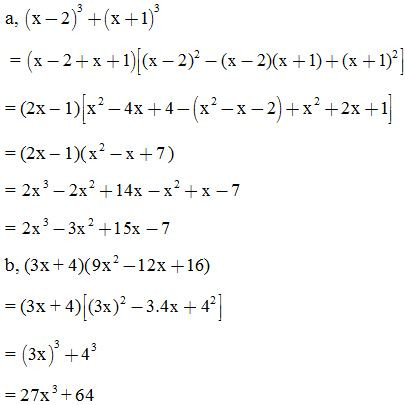
2. Dạng 2: Sử dụng hằng đẳng thức để tính nhanh

a, Phương pháp giải:

Sử dụng các hằng đẳng thức đã học để phân tích và tính

Chú ý thêm:

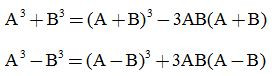
b, Ví dụ minh họa:

Tính nhanh:

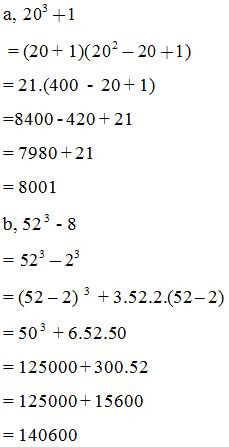
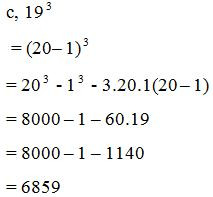
III. Bài tập tự luyện

Bài 1: Thực hiện phép tính:

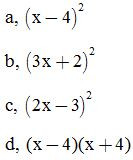
ĐS:

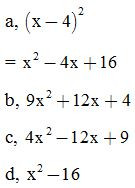
Bài 2: Thực hiện phép tính:

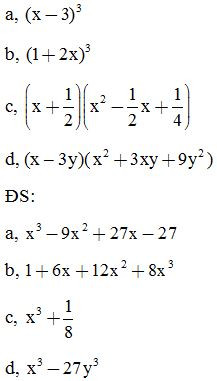
Bài 3: Viết các biểu thức dưới dạng bình phương của một tổng hoặc hiệu:

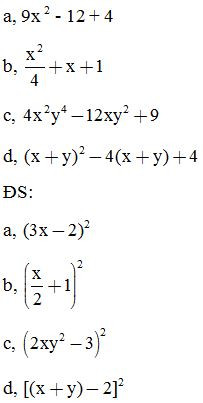
Bài 4: Chứng minh các đẳng thức sau:

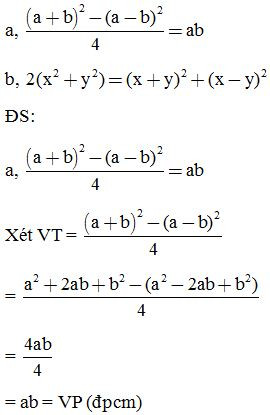
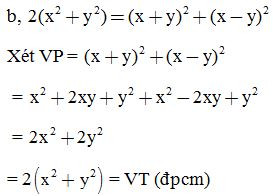
Bài 5: Rút gọn biểu thức:

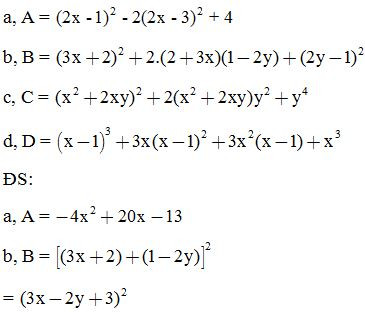
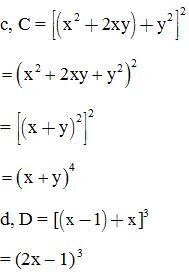
Bài 6: Rút gọn biểu thức:

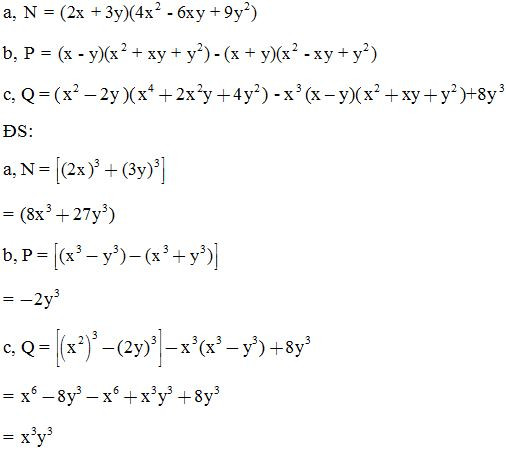
Bài 7: Tính giá trị của các biểu thức sau:

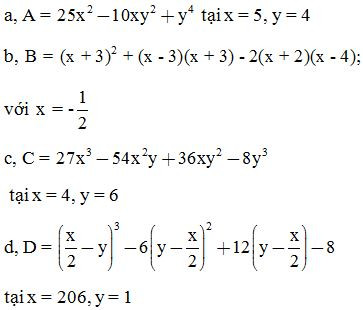
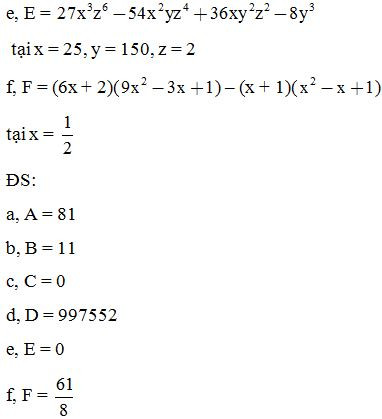
Bài 8: Tính nhanh:

a, 29²

b, 62.58

c, 102²

d, 101³

e, 91³  + 3.91² .9 + 3.91.9² + 9³

f, 18³ - 3.18² .8 + 3.18.8² - 2

g, 18³+2³

h, 23³ - 27

ĐS:

a, 29²

= (30 – 1)²

= 841

b, 62.58

= (60 + 2)(60 – 2)

= 60² - 2²

= 3596

c, 102²

= (100 + 2)²

= 10404

d, 101³

= (100 + 1)³

= 1030301

e, 91³ + 3.91² .9 + 3.91.9² + 9³

= (91 + 9)³

= 100³

= 1000000

f, 18³ - 3.18² .8 + 3.18.8² - 2⁹

 = (18 – 8)³

= 10³

= 1000

g, 18³ + 2³

= (18 + 2)³ – 3.18.2(18 + 2)

= 20³ - 6.18.20

= 5840

h, 23³ - 27

= 23³ - 3³

= (23 – 3)³ + 3.23.3.(23 – 3)

= 20³ + 9.23.20

= 12140

Bài 9: Tính giá trị biểu thức:

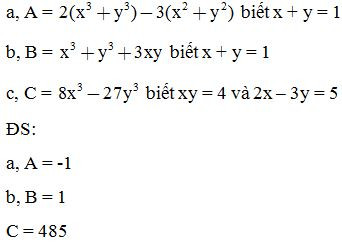
Bài 10: Chứng minh các biểu thức sau không phụ thuộc vào giá trị của biến x:

a, A =3(x – 1)² - (x + 1)² + 2(x – 3)(x + 3) – (2x + 3)² - (5 – 20x)

b, B = -x(x + 2)² + (2x + 1)² + (x + 3)(x² - 3x + 9) – 1

ĐS:

a, A = - 30

b, B = 27

Bài 11: Tính giá trị nhỏ nhất của biểu thức:

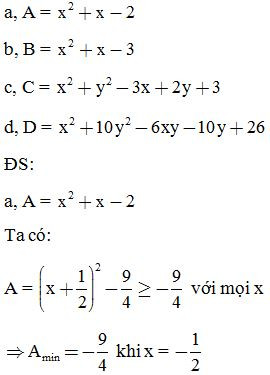
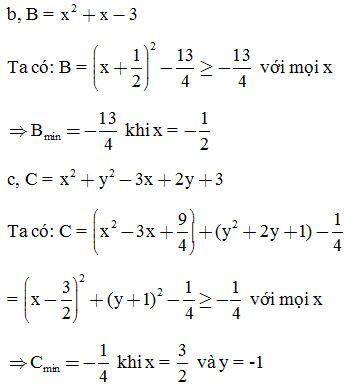
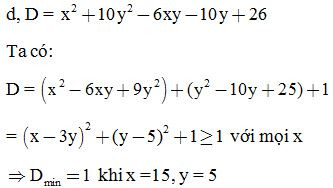
Bài 12: Tìm giá trị lớn nhất của biểu thức:

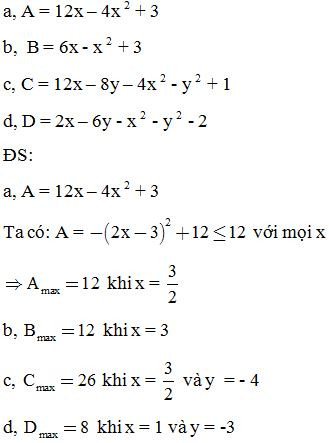
Bài 13: Chứng minh rằng với mọi a, b, c ta luôn có:

(a + b + c)³ = a³ + b³ + c³ + 3(a + b)(b + c)(c + a)

ĐS: Hướng dẫn:

Đặt a + b = A, B = c

Ta có: VT = (a + b + c)³

= (A + B)³ = A³ + B + 3A²B + 3AB²

Thay vào ta được:

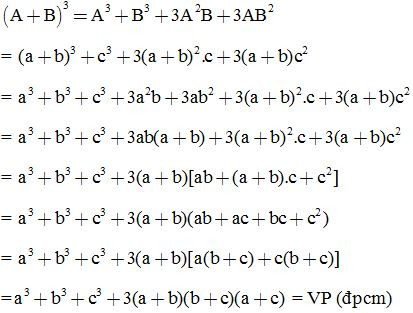
Bài 14: Biến đổi các biểu thức sau bằng việc áp dụng các hằng đẳng thức

a, (x + 2y)2

b, (x – 3y)(x + 3y)

c, (5 – x)2

d, (x – 1)2

e, (3 – y)2

f, (x – 1/2)2

Trả lời:

a, (x + 2y)2 = x2 + 4xy + 4y2

b, (x – 3y)(x + 3y) = x2 – (3y)2 = x2 – 9y2

c, (5 – x)2 = 52 – 10x + x2 = 25 – 10x + x2

d, (x – 1)2 = x2 – 2x + 1

e, (3 – y)2 = 9 – 6y + y2

f, (x – 1/2)2 = x2 – x + 1/4

Bài 15: Rút gọn biểu thức:

a, (x + y)2 + (x – y)2

b, 2(x – y)(x + y) + (x + y)2 + (x – y)2

c, (x – y + z)2 + (z – y)2 + 2(x – y + z)(y – z)

Trả lời:

a, (x + y)2 + (x – y)2

= x2 + 2xy + y2 + x2 – 2xy + y2

= 2x2 + 2y2

b, 2(x – y)(x + y) + (x + y)2 + (x – y)2

= [(x + y) + (x – y)]2 = (2x)2 = 4x2

c, (x – y + z)2 + (z – y)2 + 2(x – y + z)(y – z)

= (x – y + z)2 + 2(x – y + z)(y – z) + (y – z)2

= [(x – y + z) + (y – z)]2 = x2

Bài16: Tính giá trị của các biểu thức sau trên cơ sở áp dụng các hằng đẳng thức đã học

a, x2 – y2 tại x = 87 và y = 13

b, x3 + 9x2+ 27x + 27 tại x = 97

Trả lời:

a, Ta có: x2 – y2 = (x + y)(x – y)

Thay x = 87, y = 13, ta được:

x2 – y2 = (x + y)(x – y)

= (87 + 13)(87 – 13)

= 100.74 = 7400

b, Ta có: x3 + 9x2 + 27x + 27

= x3 + 3.x2.3 + 3.x.32 + 33

= (x + 3)3

Thay x = 97, ta được: (x + 3)3 = (97 + 3)3 = 1003 = 1000000

Bài 17: Chứng minh rằng:

(a + b)(a2 – ab + b2) + (a – b)(a2 + ab + b2) = 2a3

Trả lời:

 Ta có: (a + b)(a2 – ab + b2) + (a – b)(a2 + ab + b2)

= a3 + b3 + a3 – b3 = 2a3

Như vậy, vế trái bằng vế phải nên đẳng thức được chứng minh.

Bài 18: Áp dụng kiến thức về hằng đẳng thức để chứng tỏ rằng 4x – x2 – 5 < 0 với mọi x

Trả lời: Ta có: 4x – x2 – 5 = -(x2 – 4x + 4) – 1 = -(x – 2)2 -1

Vì (x – 2)2 ≥ 0 với mọi x nên –( x – 2)2 ≤ 0 với mọi x.

Suy ra: -(x – 2)2 - 1 ≤ 0 với mọi x

Vậy 4x – x2 – 5 < 0 với mọi x.

Bài 19: Áp dụng kiến thức về hằng đẳng thức hãy tìm giá trị nhỏ nhất của đa thức M = x2 + y2 – x + 6y + 10

Trả lời:  

Ta có: M = x2 + y2 – x + 6y + 10 = (y2 + 6y + 9) + (x2 – x + 1)

= (y + 3)2 + (x2 – 2.1/2 x + 1/4 + 3/4) = (y + 3)2 + (x – 1/2)2 + 3/4

Vì (y + 3)2 ≥ 0 và (x – 1/2)2 ≥ 0 nên (y + 3)2 + (x – 1/2)2 ≥ 0

⇒ (y + 3)2 + (x – 12)2 + 3/4 ≥ 3/4

⇒ M = 3/4 là giá trị nhỏ nhất khi (y + 3)2 =0

⇒ y = -3 và (x – 1/2)2 = 0 ⇒ x = 1/2

Vậy M = 3/4 là giá trị nhỏ nhất tại y = -3 và x = 1/2

Xem thêm các dạng bài tập hay, có đáp án:

70 Bài tập về những hằng đẳng thức đáng nhớ (có đáp án năm 2024) - Toán 8

20 Bài tập hằng đẳng thức đáng nhớ lớp 8 (2024) chi tiết nhất

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức (có đáp án năm 2024) - Toán 8

70 Bài tập về Giải bài toán bằng cách lập phương trình (có đáp án năm 2024) - Toán 8

50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2024) - Toán 9