50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2024) - Toán 9

1900.edu.vn xin giới thiệu: Căn thức bậc hai và hằng đẳng thức √A2=|A| Toán 9. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 9, giải bài tập Toán 9 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

Căn thức bậc hai và hằng đẳng thức √ A 2 = | A |

Kiến thức cần nhớ

1. Căn thức bậc hai

Với A là một biểu thức đại số, người ta gọi $\sqrt{A}$ là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.

$\sqrt{A}$ xác định (có nghĩa) khi A lấy giá trị không âm.

Ví dụ 1. $\sqrt{5 x}$ là căn thức bậc hai của 5x;

$\sqrt{5 x}$ xác định khi 5x ≥ 0, tức là khi x ≥ 0.

2. Hằng đẳng thức $\sqrt{A^{2}} = |A|$

Định lí. Với mọi số a, ta có $\sqrt{a^{2}} = |a|$ .

Ví dụ 2. Tính

a) $\sqrt{14^{2}}$ ;

b) $\sqrt{{(- 20)}^{2}}$ .

Lời giải:

a) $\sqrt{14^{2}} = |14| = 14$ .

b) $\sqrt{{(- 20)}^{2}} = |- 20| = 20$ .

Chú ý. Một cách tổng quát, với A là một biểu thức ta có $\sqrt{A^{2}} = |A|$ , có nghĩa là:

$\sqrt{A^{2}} = A$ nếu A ≥ 0 (tức là A lấy giá trị không âm);

$\sqrt{A^{2}} = - A$ nếu A < 0 (tức là A lấy giá trị âm).

Ví dụ 3. Rút gọn

a) $\sqrt{{(x - 4)}^{2}}$ với x < 4;

b) $\sqrt{a^{6}}$ với a ≥ 0.

Lời giải:

a) $\sqrt{{(x - 4)}^{2}} = |x - 4| = 4 - x$ (vì x < 4);

b) $\sqrt{a^{6}} = \sqrt{{(a^{3})}^{2}} = | a^{3} |$ .

Vì a ≥ 0 nên a³ ≥ 0, do đó | a³| = a³.

Vậy $\sqrt{a^{6}} = a^{3}$ (với a ≥ 0).

Bài tập tự luyện (có đáp án)

Bài 1: Hình chữ nhật ABCD có đường chéo AC = 5cm và cạnh BC = x (cm) thì cạnh $AB = \sqrt {25 - {x^2}} \left( {cm} \right)$ . Vì sao? (h.2)

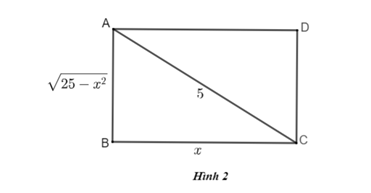
Câu hỏi 1 trang 8 SGK Toán 9 tập 1

Hướng dẫn giải:

Áp dụng định lí Pi - ta - go vào tam giác ABC vuông tại B có:

$\eqalign{& A{B^2} + B{C^2} = A{C^2} \Leftrightarrow A{B^2} + {x^2} = {5^2} \cr & \Leftrightarrow A{B^2} = 25 - {x^2} \cr & \Rightarrow AB = \sqrt {\left( {25 - {x^2}} \right)} \,\,\,\left( {do\,\,AB > 0} \right) \cr}$

Bài 2: Với giá trị nào của x thì $\sqrt {5 - 2x}$ xác định?

Hướng dẫn giải:

Điều kiện để căn thức $\sqrt {5 - 2x}$ xác định (có nghĩa) là:

$5 - 2x \geqslant 0 \Leftrightarrow 2x \leqslant 5 \Leftrightarrow x \leqslant \frac{5}{2}$

Bài 3: Điền số thích hợp vào ô trống trong bảng sau:

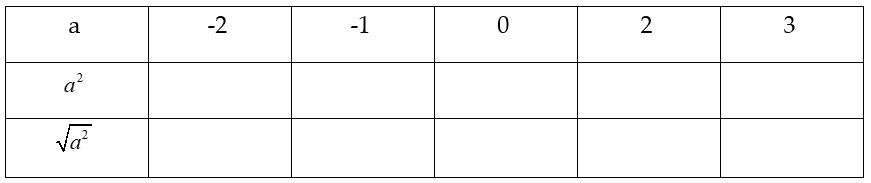
Câu hỏi 3 trang 8 SGK Toán 9 tập 1

Hướng dẫn giải:

a	-2	-1	2	3
$a^{2}$	4	1	4	9
$\sqrt{a^{2}}$	2	1	2	3

Bài 4: Với giá trị nào của a thì mỗi căn thức sau có nghĩa:

$a)\sqrt{\frac{a}{3}},$ $b) \sqrt{-5a};$ $c) \sqrt{4 - a};$ $d)\sqrt{3a + 7}$

Hướng dẫn giải:

a) Ta có: $\sqrt{\frac{a}{3}}$ có nghĩa khi $\frac{a}{3}\ge0\ \Leftrightarrow\ a\ge0$

b) Ta có: $\sqrt{-5a}$ có nghĩa khi $-5a\ge0\ \Leftrightarrow\ a\ \le\frac{0}{-5}\Leftrightarrow\ a\le0$

c) Ta có: $\sqrt{4 - a}$ có nghĩa khi $4-a\geq 0 \Leftrightarrow -a\geq -4 \Leftrightarrow a\leq 4$

d) Ta có: $\sqrt{3a + 7}$ có nghĩa khi $3a+7\geq 0\Leftrightarrow 3a \geq -7 \Leftrightarrow a\geq \frac{-7}{3}$

Bài 5: Tính

$a) \sqrt {{{\left( {0,1} \right)}^2}}$ $b) \sqrt {{{\left( { - 0,3} \right)}^2}}$

$c) - \sqrt {{{\left( { - 1,3} \right)}^2}}$ $d) - 0,4\sqrt {{{\left( { - 0,4} \right)}^2}}$

Hướng dẫn giải:

a) Ta có: $\sqrt {{{\left( {0,1} \right)}^2}} = \left| {0,1} \right| = 0,1$

b) Ta có: $\sqrt {{{\left( { - 0,3} \right)}^2}} = \left| { - 0,3} \right| = 0,3$

c) Ta có: $- \sqrt {{{\left( { - 1,3} \right)}^2}} = - \left| { - 1,3} \right| = -1,3$

d) Ta có:

$- 0,4\sqrt {{{\left( { - 0,4} \right)}^2}} = - 0,4.\left| {-0,4} \right| = - 0,4.0,4$

$= - 0,16$

Bài 6: Rút gọn các biểu thức sau:

$a)\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}};$ $b)\sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}}$

$c)\ 2\sqrt{a^2}$ với $a\ge0;$ $d)\ 3\sqrt{\left(a-2\right)^2}$ với $a < 2.$

Hướng dẫn giải:

vì $\left\{ \matrix{{2^2} = 4 \hfill \cr {\left( {\sqrt 3 } \right)^2} = 3 \hfill \cr} \right.$

mà $4>3$ nên $\sqrt{4} > \sqrt{3} \Leftrightarrow 2> \sqrt{3} \Leftrightarrow 2- \sqrt{3}>0.$

$\Leftrightarrow \left| {2 - \sqrt 3 } \right| =2- \sqrt{3}.$

Do đó: $\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} = \left| {2 - \sqrt 3 } \right|=2- \sqrt{3}$

Vì $\left\{ \matrix{{3^2} = 9 \hfill \cr {\left( {\sqrt {11} } \right)^2} = 11 \hfill \cr} \right.$

mà $9<11$ nên $\sqrt{9} < \sqrt{11} \Leftrightarrow 3< \sqrt{11} \Leftrightarrow 3- \sqrt{11} <0$

$\Leftrightarrow \left| {3 - \sqrt {11} } \right| =-(3- \sqrt{11})=-3+\sqrt{11}$

$=\sqrt{11}-3.$

Do đó: $\sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}} = \left| {3 - \sqrt {11} } \right| =\sqrt{11}-3.$

c) Ta có: $2\sqrt {{a^2}} = 2\left| a \right| = 2{\rm{a}}$ (vì $a \ge 0$ )

d) Vì $a < 2$ nên $a - 2<0$ .

$\Leftrightarrow \left| a-2 \right|=-(a-2)=-a+2=2-a$

Do đó: $3\sqrt {{{\left( {a - 2} \right)}^2}} = 3\left| {a - 2} \right| = 3\left( {2 - a} \right)$

$= 6 - 3a.$

Bài 7: Tìm x biết

a) $\sqrt{x^2}=7$

b) $\sqrt{x^2}= \left | -8 \right |$

c) $\sqrt{4^2}=7$

d) $\sqrt{9x^2}= \left |-12 \right |$

Hướng dẫn giải:

$\sqrt{7^2}=7$

$\Leftrightarrow \left |x \right | =7$

$\Leftrightarrow x=\pm 7$

$\sqrt{x^2}= \left |-8 \right |$

$\Leftrightarrow \left | x \right | =8$

$x=\pm 8$

$\sqrt{4x^2}=6$

$\Leftrightarrow\sqrt{2x^2}=6$

$\Leftrightarrow \left |2x \right | =6$

$\Leftrightarrow 2x=\pm 6$

$\Leftrightarrow =\pm 3$

$\sqrt{9x^2} = \left |-12 \right |$

$\Leftrightarrow\sqrt{3x^2}=12$

$\Leftrightarrow \left |3x \right | =12$

$\Leftrightarrow3x=\pm12$

$\Leftrightarrow x=\pm 4$

Bài 8: Chứng minh

a) $(\sqrt{3}- 1)^{2}= 4 - 2\sqrt{3};$

b) $\sqrt{4 - 2\sqrt{3}}- \sqrt{3} = -1$

Hướng dẫn giải:

a) Ta có: $VT={\left( {\sqrt 3 - 1} \right)^2} = {\left( {\sqrt 3 } \right)^2} - 2. \sqrt 3 .1 + {1^2}$

$= 3 - 2\sqrt 3 + 1$

$=(3+1)-2\sqrt 3$

$= 4 - 2\sqrt 3 = VP$

Vậy $(\sqrt{3}-1)^2=4-2\sqrt{3}(đpcm)$

b) Ta có:

VT = $\sqrt {4 - 2\sqrt 3 } - \sqrt 3 = \sqrt {\left( {3 + 1} \right) - 2\sqrt 3 } - \sqrt 3$

$= \sqrt {3 - 2\sqrt 3 + 1} - \sqrt 3$

$= \sqrt {{{\left( {\sqrt 3 } \right)}^2} - 2.\sqrt 3 .1 + {1^2}} - \sqrt 3$

$= \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} - \sqrt 3$

$= \left| {\sqrt 3 - 1} \right| - \sqrt 3.$

Lại có:

$\left\{ \matrix{ {\left( {\sqrt 3 } \right)^2} = 3 \hfill \cr {\left( {\sqrt 1 } \right)^2} = 1 \hfill \cr} \right.$

Mà $3>1 \Leftrightarrow \sqrt 3 > \sqrt 1 \Leftrightarrow \sqrt 3 > 1 \Leftrightarrow \sqrt 3 -1 > 0.$

$\Rightarrow \left| \sqrt 3 -1 \right| = \sqrt 3 -1.$

Do đó $\left| {\sqrt 3 - 1} \right| - \sqrt 3 = \sqrt 3 -1 - \sqrt 3$

$= (\sqrt 3 - \sqrt 3) -1= -1 = VP.$

Vậy $\sqrt {4 - 2\sqrt 3 } - \sqrt 3 =-1 (đpcm)$

Xem thêm các dạng Toán khác :

50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2023)

50 Bài tập Bảng căn bậc hai (có đáp án năm 2023)

50 Bài tập Biến đổi đơn giản biểu thức căn thức bậc hai (có đáp án năm 2023)

50 Bài tập Rút gọn biểu thức chứa căn thức bậc hai (có đáp án năm 2023)

50 Bài tập Căn bậc hai (có đáp án năm 2023)

Được cập nhật 05/11/2023 621 lượt xem

Bởi Nguyễn Mai Hoài

Chủ đề: toán 9 Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | Bài tập căn thức bậc hai và hằng đẳng thức √ A 2 = | A |

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Toán 9

50 Bài tập Hàm số bậc nhất (có đáp án năm 2024) - Toán 9 chi tiết nhất

1900.edu.vn xin giới thiệu: Hàm số bậc nhất Toán 9. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 9, giải bài tập Toán 9 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

1.6k 11 tháng trước

Toán 9

50 Bài tập Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án năm 2024) - Toán 9

1900.edu.vn xin giới thiệu: Một số hệ thức về cạnh và đường cao trong tam giác vuông Toán 9. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 9, giải bài tập Toán 9 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

527 11 tháng trước

Toán 9

50 Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông (có đáp án năm 2024) - Toán 9

1900.edu.vn xin giới thiệu: Một số hệ thức về cạnh và góc trong tam giác vuông Toán 9. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 9, giải bài tập Toán 9 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

634 11 tháng trước

50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2024) - Toán 9

Kiến thức cần nhớ

1. Căn thức bậc hai

2. Hằng đẳng thức A2=A

Bài tập tự luyện (có đáp án)

Bình luận (0)

Bài viết cùng chủ đề

50 Bài tập Hàm số bậc nhất (có đáp án năm 2024) - Toán 9 chi tiết nhất

50 Bài tập Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án năm 2024) - Toán 9

50 Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông (có đáp án năm 2024) - Toán 9

Nội dung bài viết

2. Hằng đẳng thức $\sqrt{A^{2}} = |A|$