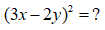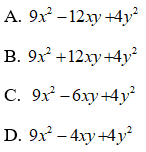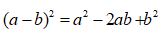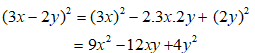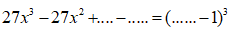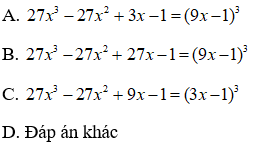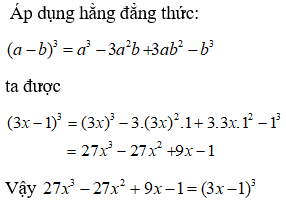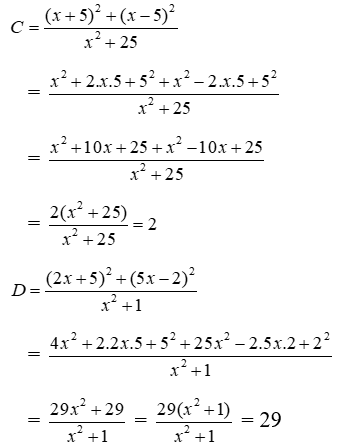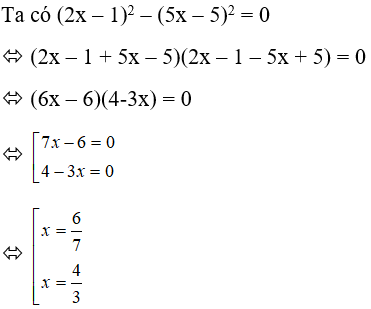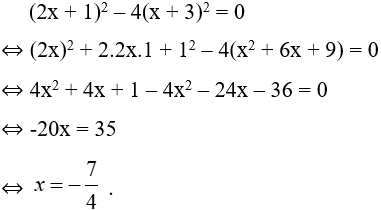20 Bài tập hằng đẳng thức đáng nhớ Toán 8

1. Phương pháp giải

1. ( a + b )² = a² + 2ab + b²

2. ( a - b )² = a² - 2ab + b²  

3. a² - b² = ( a - b )( a + b )

4. ( a + b )³ = a³ + 3a²b + 3ab² + b³

5. ( a - b )³ = a³ - 3a²b + 3ab² - b³

6. a³ + b³ = ( a + b )( a² - ab + b² )

7. a³ - b³ = ( a - b )( a² + ab + b² )  

2. Ví dụ minh họa

Ví dụ 1:

a) Tính ( 5x -y )²

b) Viết biểu thức 4x² - 4x + 1 dưới dạng bình phương của một hiệu

Lời giải:

a) Ta có ( 5x -y )² = ( 5x )² - 2.5x.y + ( y )² = 25x² - 10xy + y².

b) Ta có 4x² - 4x + 1 = ( 2x )² - 2.2x.1 + 1 = ( 2x - 1 )².

Ví dụ 2:

a) Tính ( x - 2 )( x + 2 ).

b) Tính 56.64

Lời giải:

a) Ta có: ( x - 2 )( x + 2 ) = ( x )² - 2² = x² - 4.

b) Ta có: 56.64 = ( 60 - 4 )( 60 + 4 ) = 60² - 4² = 3600 - 16 = 3584.

3. Bài tập vận dụng

Bài 1: Điền vào chỗ trống: A = ( 1/2x - y )² = 1/4x² - ... + y²

   A. 2xy   B. xy

   C. - 2xy   D. 1/2 xy

Lời giải:

Áp dụng hằng đẳng thức (a - b)² = a² - 2ab + b².

Khi đó ta có A = ( 1/2x - y )² = 1/4x² - 2.1/2x.y + y² = 1/4x² - xy + y².

Suy ra chỗ trống cần điền là xy.

Chọn đáp án B.

Bài 2: Điều vào chỗ trống: ... = ( 2x - 1 )( 4x² + 2x + 1 ).

   A. 1 - 8x³.

   B. 1 - 4x³.

   C. x³ - 8.

   D. 8x³ - 1.

Lời giải:

Áp dụng hằng đẳng thức a³ - b³ = ( a - b )( a² + ab + b² )

Khi đó ta có ( 2x - 1 )( 4x² + 2x + 1 ) = ( 2x - 1 )[ ( 2x )² + 2x.1 + 1 ] = ( 2x )³ - 1 = 8x³ - 1.

Suy ra chỗ trống cần điền là 8x³ - 1.

Chọn đáp án D.

Bài 3: Tính giá trị cuả biểu thức A = 8x³ + 12x²y + 6xy² + y³ tại x = 2 và y = -1.

   A. 1   B. 8

   C. 27   D. -1

Lời giải:

Áp dụng hằng đẳng thức ( a + b )³ = a³ + 3a²b + 3ab² + b³.

Khi đó ta có:

A = 8x³ + 12x²y + 6xy² + y³ = ( 2x )³ + 3.( 2x )².y + 3.( 2x ).y² + y³ = ( 2x + y )³

Với x = 2 và y = -1 ta có A = ( 2.2 - 1 )³ = 3³ = 27.

Chọn đáp án C.

Bài 4: Tính giá trị của biểu thức A = 35² - 700 + 10².

   A. 25².   B. 15².

   C. 45².   D. 20².

Lời giải:

Ta có A = 35² - 700 + 10² = 35² - 2.35.10 + 10²

Áp dụng hằng đẳng thức ( a - b )² = a² - 2ab + b².

Khi đó A = ( 35 - 10 )² = 25².

Chọn đáp án A.

Bài 5: Giá trị của x thỏa mãn 2x² - 4x + 2 = 0 là ?

   A. x = 1.   B. x = - 1.

   C. x = 2.   D. x = - 2.

Lời giải:

Ta có 2x² - 4x + 2 = 0 ⇔ 2( x² - 2x + 1 ) = 0        ( 1 )

Áp dụng hằng đẳng thức ( a - b )² = a² - 2ab + b²

Khi đó ta có ( 1 ) ⇔ 2( x - 1 )² = 0 ⇔ x - 1 = 0 ⇔ x = 1.

Chọn đáp án A.

Bài 6: 

Lời giải:

Áp dụng hằng đẳng thức đáng nhớ: 

Ta được:

Chọn đáp án A

Bài 7: Điền vào chỗ chấm:

Lời giải:

Chọn đáp án C

Bài 8: Rút gọn biểu thức: A = (x – 2y).(x² + 2xy + y²) - (x + 2y). (x² – 2xy + y²)

A. 2x³     B. -16y³

C. 16y³     D. –2x³

Lời giải:

Áp dụng hằng đẳng thức:

a³ – b³ = (a – b).(a² + ab + b²) và a³ + b³ = (a + b).(a² – ab + b²) ta được:

A = (x – 2y). (x² + 2xy + y²) - (x + 2y). (x² – 2xy + y²)

A = x³ – (2y)³ - [x³ + (2y)³]

A = x³ – 8y³ – x³ – 8y³ = -16y³

Chọn đáp án B

Bài 9: Tìm x biết x² – 16 + x(x – 4) = 0

A. x = 2 hoặc x = - 4.

B. x = 2 hoặc x = 4.

C. x = -2 hoặc x = - 4.

D. x = -2 hoặc x = 4.

Lời giải:

Ta có: x² – 16 + x(x – 4) = 0

⇔ (x + 4). (x - 4) + x.(x – 4) = 0

⇔ (x + 4 + x).(x - 4) = 0

⇔ (2x + 4). (x - 4) = 0

⇔ 2x + 4 = 0 hoặc x – 4 = 0

* Nếu 2x + 4 = 0 thì x = -2

* Nếu x – 4 =0 thì x = 4

Vậy x = -2 hoặc x = 4.

Chọn đáp án D

Bài 10: Rút gọn biểu thức A = (x + 2y ).(x - 2y) - (x – 2y)²

A. 2x² + 4xy     B. – 8y² + 4xy

C. - 8y²     D. – 6y² + 2xy

Lời giải:

Ta có: A = (x + 2y ). (x - 2y) - (x – 2y)²

A = x² – (2y)² – [x² – 2.x.2y +(2y)² ]

A = x² – 4y² – x² + 4xy - 4y²2

A = -8y² + 4xy

Chọn đáp án B

Bài 11: Chọn câu đúng

A. (c + d)² – (a + b)² = (c + d + a + b)(c + d – a + b)

B. (c – d)² – (a + b)² = (c – d + a + b)(c – d – a + b)

C. (a + b + c – d)(a + b – c + d) = (a + b)² – (c – d)²

D. (c – d)² – (a – b)² = (c – d + a – b)(c – d – a – b)

Lời giải

Ta có

(c + d)² – (a + b)² = (c + d + a + b)(c + d – (a + b)) = (c + d + a + b)(c + d – a – b) nên A sai

(c – d)² – (a + b)² = (c – d + a + b)[c – d – (a + b)] = (c – d + a + b)(c – d – a – b) nên B sai

(c – d)² – (a – b)² = (c – d + a – b)(c – d – (a – b)) = (c – d + a – b)(c – d – a + b) nên D sai

(a + b + c – d)(a + b – c + d) = [(a + b) + (c – d)][(a + b) – (c – d)] = (a + b)² – (c – d)² nên C đúng

Đáp án cần chọn là: C

Bài 12: Chọn câu đúng

A. 4 – (a + b)² = (2 + a + b)(2 – a + b)

B. 4 – (a + b)² = (4 + a + b)(4 – a – b)

C. 4 – (a + b)² = (2 + a – b)(2 – a + b)

D. 4 – (a + b)² = (2 + a + b)(2 – a – b)

Lời giải

Ta có 4 – (a + b)² = 2² – (a + b)² = (2 + a + b)[2 – (a + b)]

                                                = (2 + a + b)(2 – a – b)

Đáp án cần chọn là: D

Bài 13: Rút gọn biểu thức A = (3x – 1)² – 9x(x + 1) ta được

A. -15x + 1 

B. 1            

C. 15x + 1            

D. – 1

Lời giải

Ta có A = (3x – 1)² – 9x(x + 1)

          = (3x)² – 2.3x.1 + 1 – (9x.x + 9x)

          = 9x² – 6x + 1 – 9x² – 9x

          = -15x + 1

Đáp án cần chọn là: A

Bài 14: Rút gọn biểu thức A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4), ta được2 ^{+ 4(x – 5)}2 ^{– 9(}

A. 342        

B. 243        

C. 324        

D. -324

Lời giải

Ta có A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4)

          = 5(x² + 2.x.4 + 16) + 4(x² – 2.x.5 + 5²) – 9(x² – 4²)

          = 5(x² + 8x + 16) + 4(x² – 10x + 25) – 9(x² – 4²)

          = 5x² + 40x + 80 + 4x² – 40x + 100 – 9x² + 144

=

(5x² + 4x² – 9x²) + (40x – 40x) + (80 +100 + 144)

          = 324

Đáp án cần chọn là: C

Bài 15: Rút gọn biểu thức B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7) ta được

A. 0            

B. 1            

C. 19          

D. – 19

Lời giải

Ta có B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7)

          = 2a² + 2a – 3a – 3 – (a² – 8a + 16) – (a² + 7a)

          = 2a² + 2a – 3a – 3 – a² + 8a – 16 – a² – 7a

          = - 19

Đáp án cần chọn là: D

Bài 16: Cho B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1). Chọn câu đúng.

A. B < 12   

B. B > 13   

C. 12 < B< 14

D. 11 < B < 13

Lời giải

Ta có B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1).

          = (x²)² +2.x².4 + 3² – (x².x² + x².3) – 3(x² – 1)       

          = x⁴ + 6x² + 9 – x⁴ – 3x² – 3x² + 3 = 12

Đáp án cần chọn là: D

Bài 17: Cho 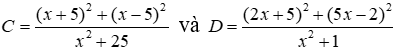. Tìm mối quan hệ giữa C và D.

A. D = 14C + 1

B. D = 14C 

C. D = 14C – 1

D. D = 14C – 2

Lời giải

Ta có:

Vậy D = 29; C = 2 suy ra D = 14C + 1 (do 29 = 14.2 + 1)

Đáp án cần chọn là: A

Bài 18: Cho M = 4(x + 1)² +  (2x + 1)² – 8(x – 1)(x + 1) – 12x và N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14).

Tìm mối quan hệ giữa M và N

A. 2N – M = 60

B. 2M – N = 60

C. M> 0, N < 0

D. M > 0, N > 0

Lời giải

Ta có

M = 4(x + 1)² +  (2x + 1)² – 8(x – 1)(x + 1) – 12

= 4(x² + 2x + 1) + (4x² + 4x + 1) – 8(x² – 1) – 12x

= 4x² + 8x + 4 + 4x² + 4x + 1 – 8x² +8 – 12x

= (4x² + 4x² – 8x²) + (8x + 4x – 12x) + 4 + 1 +8

= 13

N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14)

= 2(x² – 2x + 1) – 4(9 + 6x + x²) + 2x² + 28x

= 2x² – 4x + 2 – 36 – 24x – 4x² + 2x² + 28x

= (2x² +2x² – 4x²) + (-4x – 24x + 28x) + 2 – 36

= -34

Suy ra M = 13, N = -34 ⇔ 2M – N = 60

Đáp án cần chọn là: B

Bài 19: Có bao nhiêu giá trị x thỏa mãn (2x – 1)² – (5x – 5)² = 0

A. 0            

B. 1            

C. 2            

D. 3

Lời giải

Vậy có hai giá trị của x thỏa mãn yêu cầu

Đáp án cần chọn là: C

Bài 20: Có bao nhiêu giá trị x thỏa mãn (2x + 1)² – 4(x + 3)² = 0

A. 0            

B. 1            

C. 2            

D. 3

Lời giải

Ta có:

Vậy có một giá trị của x thỏa mãn yêu cầu.

Đáp án cần chọn là: B

Xem thêm các dạng bài tập khác:

70 Bài tập về những hằng đẳng thức đáng nhớ (có đáp án năm 2023)

50 bài tập về những hằng đẳng thức đáng nhớ (có đáp án 2023)

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức (có đáp án năm 2024)

50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2024)

20 Bài tập về Bất đẳng thức Cô-si và hệ quả (2024)