50 bài tập Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp có đáp án năm 2024 Toán 8

Bài giảng Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

Lý thuyết

Khái niệm: Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

Khi thực hiện phân tích đa thức thành nhân tử các biểu thức phức tạp ta thường sử dụng phối hợp cả ba phương pháp phân tích đa thức thành nhân tử cơ bản: phương pháp nhân tử chung, phương pháp hằng đẳng thức, phương pháp nhóm hạng tử.

Chú ý: 

- Nếu các hạng tử của đa thức có nhân tử chung thì ta nên sử dụng phương pháp đặt nhân tử chung trước để đa thức trở lên đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.

- Nếu các hạng tử của đa thức có nhân tử chung, ta nên đặt nhân tử chung ra ngoài dấu ngoặc ( ) để đa thức trong ( ) đơn giản hơn rồi mới tiếp tục phân tích đến cuối cùng khi không còn phân tích được nữa.

Ví dụ: Phân tích đa thức x³y + 6x²y² + 9xy thành nhân tử.

Hướng dẫn giải

x³y + 6x²y² + 9xy

= xy(x² + 6xy + 9)

= xy(x² + 2.xy.3 + 3²)

= xy(x + 3)²

Các dạng bài tập phân tích đa thức thành nhân tử bằng các phối hợp nhiều phương pháp

Dạng 1: Phân tích đa thức thành nhân tử bằng cách phối hợp các phương pháp cơ bản

1. Phương pháp giải

Sử dụng phối hợp nhiều phương pháp cơ bản để phân tích đa thức thành nhân tử:

+ Phương pháp nhân tử chung

+ Phương pháp hằng đẳng thức

+ Phương pháp nhóm hạng tử

2. Bài tập minh họa

Ví dụ 1: Phân tích các đa thức sau thành nhân tử:

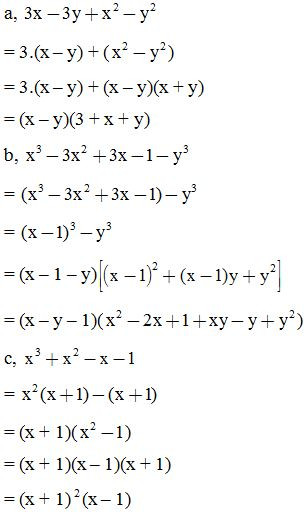
Ví dụ 2: Phân tích đa thức thành nhân tử:

a)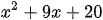 

b)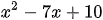 

c)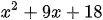 

d)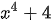 

e)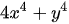 

Hướng dẫn giải

a) 

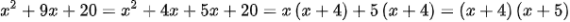
b) 

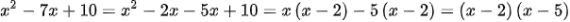
c) 

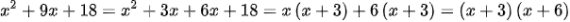
d)

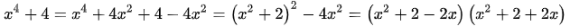
e) 

.

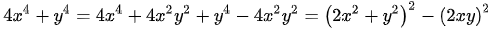
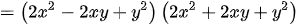Dạng 2: Phân tích đa thức thành nhân tử bằng phương pháp tách hạng tử

1. Phương pháp giải

Tách một hạng tử thành nhiều hạng tử sau đó sử dụng phương pháp nhóm hạng tử để phân tích.

Chú ý:  Đối với các đa thức có dạng $a{x}^2+bx+c (a\ne 0)$ ta thường sử dụng cách tách sau để phân tích đa thức thành nhân tử:

+ Cách 1: Tách $bx=b_{1}x+b_{2}x$ sao cho $b_1{b}_2=ac$

+ Cách 2: Tách c =$c_1+c_2$ sao cho $a{x}^2+bx+c_1=$${(\mathrm{...}\pm \mathrm{...})}^2$

2. Bài tập minh họa

a) Đối với đa thức bậc hai f(x) = ax² + bx + c có nghiệm

Phương pháp chung

Bước 1: Tìm tích ac rồi phân tích ac ra tích của hai thừa số nguyên bằng mọi cách

Bước 2: Chọn hai thừa số trong các tích trên có tổng bằng b

Bước 3: Tách bx = a_ix + c_ix. Từ đó nhóm hai số hạng thích hợp để phân tích tiếp

Ví dụ 1: Phân tích đa thức f(x) = 3x²+ 8x + 4 thành nhân tử

Hướng dẫn giải

Phân tích ac:

ac = 12 = 3.4 = (-3).(-4) = 2.6 = (-2). (-6) = 1.12 = (-1).(-12)

Tích của hai thừa số có tổng bằng b = 8 là tích ac = 2.6

Tách 8x = 2x + 6x

=> 3x² + 8x + 4 = 3x² + 2x + 6x + 4 = (3x² + 2x) + (6x + 4)

= x(3x + 2) + 2(3x + 2) = (x + 2)(3x + 2)

b) Đối với đa thức hai biến dạng f(x; y) = ax² + bxy + cy²

Phương pháp chung

Phương pháp 1: Xem đa thức f(x; y) = ax² + bxy + cy² là đa thức một biến x

Khi đó hệ số lần lượt là a, by, xy² và ta áp dụng phương pháp như với đa thức bậc hai một biến.

Phương pháp 2: Viết đa thức về dạng . Đặt  và phân tích đa thức at² + bt + c theo phương pháp như với đa thức bậc hai một biến.

Ví dụ 2: Phân tích đa thức 2x² – 5xy + 2y² thành nhân tử

Hướng dẫn giải

Cách 1: Xét đa thức f(x) = 2x² – 5xy + 2y²

Khi đó ta có a = 2; b = -5y; c = 2y²

Ta có ac = y.4y = (-y).(-4y) = 2y.2y = (-2y).(-2y) = ….

Ta chọn tích (-y).(-4y) vì (-y) + (-4y) = -5y = b

=> 2x² – 5xy + 2y² = 2x² – xy – 4xy + 2y² = x(2x – y) – 2y(2x – y) = (x – 2y)(2x – y)

Cách 2: Xét đa thức 

Đặt \[t = \frac{x}{y}\] và ta có đa thức 2t² – 5t + 2 = 2t² – t – 4t + 2 = (2t – 1)(t – 2)

Khi đó ta được f(x; y) = y²(2t – 1)(t – 2) =  = (2x – y)(x – 2y)

Chú ý: Quy tắc dấu ngoặc

Khi bỏ dấu ngoặc có dấu "−" đứng trước, ta phải đối dấu tất cả các số hạng trong dấu ngoặc: dấu "−“ thành dấu "+" và dấu "+” thành dấu "−". Khi bỏ dấu ngoặc có dấu "+" đứng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên.

Ví dụ 3: Phân tích các đa thức sau thành nhân tử:

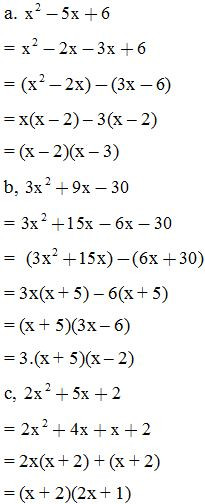
Dạng 3: Phân tích đa thức thành nhân tử bằng phương pháp đặt biến phụ

1. Phương pháp giải

Đặt các hạng tử giống nhau thành biến mới để đưa các đa thức đã cho ở đề bài về một đa thức mới với biến vừa đặt sau đó sử dụng các phương pháp phân tích đã học ở trên để phân tích đa thức thành nhân tử.

2. Bài tập minh họa

Ví dụ 1: Phân tích các đa thức sau thành nhân tử: 

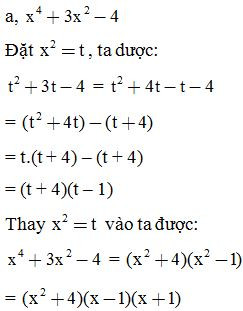
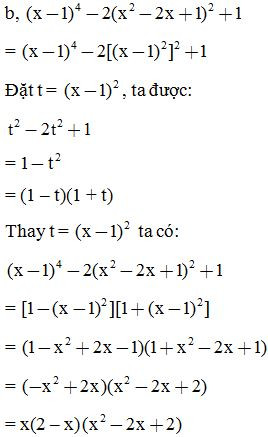
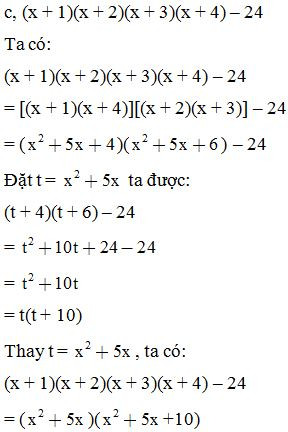
Bài tập phân tích đa thức thành nhân tử

Bài tập 1: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp:

a. 

b. 

c. 

d. 

e. 

f. 

g. 

h. 

i.

k. 

Bài tập 2: Phân tích đa thức thành nhân tử (bằng cách phối hợp nhiều phương pháp):

a. 

b. 

c. 

Bài tập 3: Tìm x:

a. 

b. 

c. 

Bài tập 4: Tính nhanh giá trị biểu thức:

a.  tại x = 49,75

b.  tại x = 93 và y = 6

Bài toán 5: Phân tích đa thức thành nhân tử :

a) 16x⁴(x – y) – x + y

b) 2x³y – 2xy³ – 4xy² – 2xy

c) x(y² – z²) + y(z² – x²) + z(x² – y²)

d) 16x³ – 54y³

e) 5x² – 5y²

f) 16x³y + yz³

g) 2x⁴ – 32

Bài toán 6: Phân tích đa thức sau thành nhân tử:

a) 4x – 4y + x² – 2xy + y²

b) x⁴ – 4x³ – 8x² + 8x

c) x³ + x² – 4x – 4

d) x⁴ – x² + 2x – 1

e) x⁴ + x³ + x² + 1

f) x³ – 4x² + 4x – 1

g) x³ + x²y – xy² – y³

h) x²y² + 1 – x² – y²

i) x² – y² – 4x + 4y

j) x² – y² – 2x – 2y

k) x² – y² – 2x – 2y

l) x³ – y³ – 3x + 3y

Bài toán 7: Tìm  x, biết.

a) x³ – x² – x + 1 = 0

b) (2x³ – 3)² – (4x² – 9) = 0

c) x⁴ + 2x³ – 6x – 9 = 0

d) 2(x + 5) – x² – 5x = 0

Bài toán 8: Tìm giá trị nhỏ nhất của biểu thức :

a) A = x² – x + 1                                                      

d) D = x² + y² – 4(x + y) + 16

b) B = 4x² + y² – 4x – 2y + 3                                  

e) E = x² + 5x + 8

c) C = x² + x + 1     

g) G = 2x² + 8x + 9

Bài toán 9: Tìm giá trị lớn nhất của biểu thức :

a) A = -4x² – 12x

b) B = 3 – 4x – x²

c) C = x²  + 2y² + 2xy – 2y

d) D = 2x – 2 – 3x²

e) E = 7 – x² – y² – 2(x + y)

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

75 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung (có đáp án năm 2024)

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức (có đáp án năm 2024)

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử (có đáp án năm 2024)

50 Bài tập phân tích đa thức thành nhân tử bằng các phối hợp nhiều phương pháp (có đáp án năm 2024)

50 bài tập về các phương pháp phân tích đa thức thành nhân tử (có đáp án 2024)