75 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung (có đáp án năm 2024) - Toán 8

1900.edu.vn xin giới thiệu: Tổng hợp các dạng bài tập phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung Toán 8. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 8, giải bài tập Toán 8 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

Bài giảng Toán 8 Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Lý thuyết

Khái niệm:Phân tích đa thức thành nhân tử (hay thừa số)là biến đổi đa thức đó thành một tích của những đa thức.

A.B + A.C + A.D = A(B + C – D)

+ Tìm nhân tử chung là đơn hoặc đa thức có mặt trong tất cả các hạng tử

+ Phân tích mỗi hạng tử thành tích các nhân tử chung và một nhân tử khác.

+ Viết nhân tử chung ra ngoài hoặc dấu ngoặc, viết các nhân tử còn lại của mỗi hạng tử vào trong dấu ngoặc (kể cả dấu của chúng).

Quy tắc dấu ngoặc

Khi bỏ dấu ngoặc có dấu "−" đứng trước, ta phải đối dấu tất cả các số hạng trong dấu ngoặc: dấu "−“ thành dấu "+" và dấu "+” thành dấu "−". Khi bỏ dấu ngoặc có dấu "+" đứng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên.

Ví dụ 1:

a) x² – 3x = x.x – 3.x = x(x – 3).

b) (y + 3)² + 3(y + 3) = (y + 3).(y + 3) + 3.(y + 3) = (y + 3)(y + 3 + 3) = (y + 3)(y + 6).

Chú ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử (lưu ý tới tính chất A = – (– A)).

Ví dụ 2:

3(x – y ) – 10x(y – x) = 3(x – y ) + 10x(x – y) = (x – y)(3 + 10x).

Các dạng bài tập về phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Dạng 1: Phân tích đa thức thành nhân tử

1. Phương pháp giải

Phân tích các hạng tử của đa thức để chọn nhân tử chung thích hợp, sau đó áp dụng tính chất phân phối của phép nhân với phép cộng

2. Bài tập minh họa:

Ví dụ 1: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung:

a. x(x - y) - 3x + 3y

b. $- a{x^2} - ax - a$

c. $2axy - 4{a^2}x{y^2} + 6{a^3}{x^2}$

d. $5{a^2}xy - 10{a^3}x - 15ay$

e. $- 3{x^2}{y^2} - 6{x^3}{y^2} - {x^2}{y^2}$

Hướng dẫn giải

a. x(x - y) - 3x + 3y

= x(x - y) - 3(x – y)

= (x – y)(x – 3)

b. $- a{x^2} - ax - a = - a\left( {{x^2} + x + 1} \right)$

c. $2axy - 4{a^2}x{y^2} + 6{a^3}{x^2} = 2ax\left( {y - 2a{y^2} + 3{a^2}x} \right)$

d. $5{a^2}xy - 10{a^3}x - 15ay = 5a\left( {axy - 2{a^2}x - 3y} \right)$

e. $- 3{x^2}{y^2} - 6{x^3}{y^2} - {x^2}{y^2} = \left( { - 3{x^2}{y^2} - {x^2}{y^2}} \right) - 6{x^3}{y^2}$

$= - 4{x^2}{y^2} - 6{x^3}{y^2} = - 2{x^2}{y^2}\left( {2 + 3x} \right)$

Ví dụ 2: Phân tích các đa thức sau thành nhân tử:

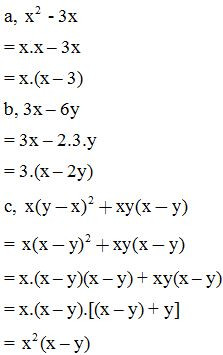
Các phương pháp phân tích đa thức thành nhân tử chi tiết nhất – Toán lớp 8 (ảnh 1)

Dạng 2: Các bài toán liên quan

1. Phương pháp giải

Phân tích các hạng tử của đa thức để chọn nhân tử chung thích hợp, sau đó áp dụng tính chất phân phối của phép nhân với phép cộng để làm một số bài toán tính nhanh, tính giá trị biểu thức, tìm x,…

2. Bài tập minh họa

Ví dụ 1: Tính nhanh:

a, 75.20,9 + 5² .20,9

= 20,9.(75 + 5²)

= 20,9.100

= 2090

b, 98,6.199 – 990.9,86

= 98,6.199 – 99.10.9,86

= 98,6.199 – 98,6.99

= 98,6.(199 – 99)

= 98,6.100

= 9860

Ví dụ 2: Tính giá trị biểu thức:

a, A = a(b + 3) – b(3 + b) tại a = 2, b = 3

A = a(b + 3) – b(b + 3)

= (b + 3)(a – b)

Thay a = 2, b = 3 vào biểu thức A ta được:

A = (3 + 3)(2 – 3) = - 6

b, B = b² - 8b – c(8 – b) tại b = 1, c = 2

Ta có:

B = b² - 8b – c(8 – b)

= -b(8 – b) – c(8 – b)

= (8 – b)(- b – c)

Thay b = 1, c = 2 vào biểu thức B, ta được:

B = (8 – 1)(- 1 – 2)

= -21

Ví dụ 3: Tìm x, biết:

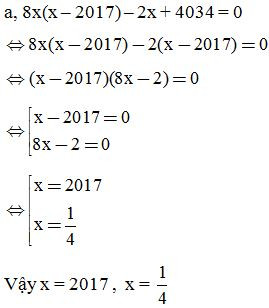
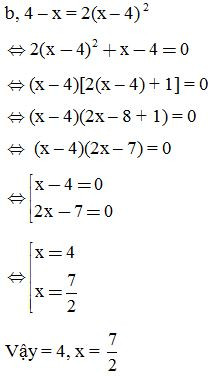
Các phương pháp phân tích đa thức thành nhân tử chi tiết nhất – Toán lớp 8 (ảnh 1)

Ví dụ 4: Tìm các cặp số nguyên (x; y) thỏa mãn một trong các đẳng thức sau:

a) x + y = xy

b) xy – x + 2(y – 1) = 13

Hướng dẫn giải

a) x + y = xy

Ta viết lại biểu thức: xy – x – y = 0

=> x(y – 1) – (y – 1) = 1 hay (y – 1)(x – 1) = 1

Mà 1 = 1.1 = (-1)(-1)

=> $\left\{ {\begin{array}{*{20}{c}} {y - 1 = 1} \\ {x - 1 = 1} \end{array}} \right.$ hoặc $\left\{ {\begin{array}{*{20}{c}} {y - 1 = - 1} \\ {x - 1 = - 1} \end{array}} \right.$

Do đó: $\left\{ {\begin{array}{*{20}{c}} {x = 2} \\ {y = 2} \end{array}} \right.$ hoặc $\left\{ {\begin{array}{*{20}{c}} {x = 0} \\ {y = 0} \end{array}} \right.$

Vậy ta có hai cặp số nguyên cần tìm là (0; 0) và (2; 2)

b) xy – x + 2(y – 1) = 13

Phân tích vế trái ra thừa số ta có:

xy – x + 2(y – 1)

= x(y - 1) + 2(y - 1)

= (y – 1)(x + 2)

Vế phải bằng 13 = 1 . 13 = 13 . 1 = (-1)(-13) = (-13).(-1) nên ta lần lượt có:

$\left\{ {\begin{array}{*{20}{c}} {y - 1 = 1} \\ {x + 2 = 13} \end{array}} \right.;\left\{ {\begin{array}{*{20}{c}} {y - 1 = 13} \\ {x + 2 = 1} \end{array}} \right.;\left\{ {\begin{array}{*{20}{c}} {y - 1 = - 1} \\ {x + 2 = - 13} \end{array}} \right.;\left\{ {\begin{array}{*{20}{c}} {y - 1 = - 13} \\ {x + 2 = - 1} \end{array}} \right.$

Hay

$\left\{ {\begin{array}{*{20}{c}} {x = 11} \\ {y = 2} \end{array}} \right.;\left\{ {\begin{array}{*{20}{c}} {x = - 1} \\ {y = 14} \end{array}} \right.;\left\{ {\begin{array}{*{20}{c}} {x = - 15} \\ {y = 0} \end{array}} \right.;\left\{ {\begin{array}{*{20}{c}} {x = - 3} \\ {y = - 12} \end{array}} \right.$

Vậy ta có 4 cặp số nguyên cần tìm là (11; 2), (-1; 14); (-15; 0); (-3; -12)

Dạng 3: Chứng minh các bài toán số nguyên:

1. Phương pháp giải

Phân tích các biểu thức đã cho một cách hợp lí thành các tích và sử dụng tính chất chia hết của số nguyên.

2. Bài tập minh họa

Ví dụ 1: Chứng minh:

a, 25ⁿ⁺¹- 25ⁿ chia hết cho 100 với mọi số tự nhiên n $\neq 0$

Hướng dẫn giải

Ta có:

25ⁿ⁺¹- 25ⁿ

= 25ⁿ (25 – 1)

= 24.25ⁿ

Ta lại có: 24 = 4.6

25ⁿ = 25.25^n-1

$\Rightarrow$ 25ⁿ⁺¹- 25ⁿ= 4.6.25.25^n-1

= 100.6.25 $⋮$ 100 với mọi $n \in ℕ^{*}$

Vậy 25ⁿ⁺¹- 25ⁿ chia hết cho 100 với mọi số tự nhiên n

b, n²(n - 1) - 2n(n - 1) chia hết cho 6 với mọi số nguyên n

Ta có:

n²(n - 1) - 2n(n - 1)

= (n – 1)(n² - 2n)

= (n – 1).n.(n – 2)

= (n – 2).(n – 1).n

Ta có: n – 2, n – 1, n là 3 số tự nhiên liên tiếp nên tích của chúng sẽ chia hết 6

$\Rightarrow$ n²(n - 1) - 2n(n - 1) chia hết cho 6 với mọi số nguyên n.

c, 50ⁿ⁺² - 50ⁿ⁺¹ chia hết cho 245 với mọi số tự nhiên n.

Ta có:

50ⁿ⁺² - 50ⁿ⁺¹

= 50ⁿ(50² - 50)

= 50ⁿ(2500 – 50)

= 2450.50ⁿ

= 245.10.50ⁿ $⋮$ 245 với mọi STN n

Vậy 50ⁿ⁺² - 50ⁿ⁺¹ chia hết cho 245 với mọi số tự nhiên n.

Ví dụ 2: Chứng minh rằng với mọi số nguyên n thì

a) 24^{n + 1} – 24ⁿ ⋮ 23

b) n²(n – 1) – 2n(n – 1) ⋮ 6

Hướng dẫn giải

a) Ta có:

24^{n + 1} – 24ⁿ

= 24ⁿ . 24 – 24ⁿ . 1

= 24ⁿ . (24 – 1)

= 24ⁿ . 23 ⋮ 23

=> 24^{n + 1} – 24ⁿ ⋮ 23 (điều phải chứng minh)

b) Ta có:

n²(n – 1) – 2n(n – 1)

= (n – 1)(n² – 2n)

= (n – 1).n.(n – 2)

= (n – 2)(n – 1)n

Đây là 3 số nguyên liên tiếp

=> (n – 2)(n – 1)n ⋮ 6

=> b) n²(n – 1) – 2n(n – 1) ⋮ 6 (điều phải chứng minh)

Luyện tập phân tích đa thức thành nhân tử

Bài tập tự luận

Bài tập 1: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung:

a. $3{x^2} + 3x$	b. ${x^2} + xy + x$
c. $x\left( {x - y} \right) + y\left( {y - x} \right)$	d. $- 3xy\left( {x - 1} \right) + 5x\left( {x - 1} \right)$
e. $3x\left( {x - 5} \right) - x + 5$	f. $- x - y + \left( {3x - 2} \right)\left( {x + y} \right)$
g. $4xy\left( {x + 2y} \right) + 8y\left( {x - 1} \right)$	h. $4\left( {x + 2} \right) - 2\left( {x + 2} \right)$
i. $\left( {5x - 1} \right)\left( {x + 4} \right) - x - 4$	k. $3x\left( {x - 2} \right) - x + 2$
m, $3\left( {x + y} \right) - {\left( {x + y} \right)^2}$	n, $\left( {x - y} \right)\left( {x + y} \right) - 4xy + 4{y^2}$
x, ${x^3} - {x^2} - 5x + 5$	y, $3ab\left( {x - 4} \right) + 9a\left( {4 - x} \right)$
z, $2{a^2}b\left( {x + y} \right) - 4{a^3}b\left( { - x - y} \right)$	t, $16{a^2} - 24a$

Bài tập 2: Phân tích đa thức thành nhân tử (bằng phương pháp đặt nhân tử chung)

a. ${x^2}\left( {x + 2} \right) - x\left( {x + 2} \right)$

b. $a\left( {m + n} \right) - 3m - 3n$

c. $10{x^2}{y^3} - 5{x^2}{y^2} + 15{x^3}{y^3}$

Bài tập 3: Phân tích đa thức sau thành nhân tử:

a. $5{x^2}{y^2} + 20{x^2}y + 35x{y^2}$

b. $3x\left( {x - 2y} \right) + 6y\left( {2y - x} \right)$

Bài tập 4: Tìm x:

a. ${x^2} + 6x = 0$

b. ${x^3} - x = 0$

c. $\left( {x - 2} \right) = {\left( {x - 2} \right)^2}$

d, $2\left( {x + 3} \right) - x\left( {x + 3} \right) = 0$

e, $16x\left( {x - 1} \right) - 32\left( {x - 1} \right) = 0$

Bài tập trắc nghiệm

Câu 1: Phân tích đa thức ${x^3} - 2{x^2}y + x{y^2}$ thành nhân tử ta được

A. $x{\left( {x - y} \right)^2}$	B. ${x^2}{\left( {x - y} \right)^2}$
C. $x\left( {x - y} \right)$	D. ${x^2}\left( {x - y} \right)$

Câu 2: Phân tích đa thức ${x^2} - 9 + 2\left( {x + 3} \right)$ thành nhân tử ta được:

A. $\left( {x - 3} \right)\left( {x - 1} \right)$	B. $\left( {x - 3} \right)\left( {x + 1} \right)$
C. $\left( {x + 3} \right)\left( {x - 1} \right)$	D. $\left( {x + 3} \right)\left( {x + 1} \right)$

Câu 3: Phân tích đa thức ${x^2} - 3x + xy - 3y$ thành nhân tử ta được:

A. $\left( {x + y} \right)\left( {x + 3} \right)$	B. $\left( {x - 3} \right)\left( {x + y} \right)$
C. $\left( {x - y} \right)\left( {x + 3} \right)$	D. $\left( {x - y} \right)\left( {x - 3} \right)$

Câu 4: Nhân tử chung của biểu thức $2\left( {x + y} \right) - 5y\left( {x + y} \right)$ là:

A. $x + y$

B. $x - y$

C. ${x^2} - {y^2}$

D. ${x^3} - {y^3}$

Câu 5: Có bao nhiêu giá trị x thỏa mãn

A. 2

B. 3

C. 4

D. 5

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

75 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung (có đáp án năm 2024)

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức (có đáp án năm 2024)

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử (có đáp án năm 2024)

50 Bài tập phân tích đa thức thành nhân tử bằng các phối hợp nhiều phương pháp (có đáp án năm 2024)

50 bài tập về các phương pháp phân tích đa thức thành nhân tử (có đáp án 2024)

Được cập nhật 20/09/2023 2k lượt xem

Bởi Quynh Anh

Chủ đề: Giáo dục

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Toán 8

65 bài tập nhân đa thức với đa thức (có đáp án năm 2024) - Toán 8

1900.edu.vn xin giới thiệu: Tổng hợp các dạng bài tập nhân đa thức với đa thức Toán 8. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 8, giải bài tập Toán 8 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

378 6 tháng trước

Toán 8

85 Bài tập về chia đa thức cho đơn thức (có đáp án 2024) - Toán 8

1900.edu.vn xin giới thiệu: Tổng hợp các dạng bài tập chia đa thức cho đơn thức Toán 8. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 8, giải bài tập Toán 8 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

583 6 tháng trước

Toán 8

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8

261 6 tháng trước

75 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung (có đáp án năm 2024) - Toán 8

Lý thuyết

Các dạng bài tập về phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung

Dạng 1: Phân tích đa thức thành nhân tử

Dạng 2: Các bài toán liên quan

Dạng 3: Chứng minh các bài toán số nguyên:

Luyện tập phân tích đa thức thành nhân tử

Bài tập tự luận

Bài tập trắc nghiệm

Bình luận (0)

Bài viết cùng chủ đề

65 bài tập nhân đa thức với đa thức (có đáp án năm 2024) - Toán 8

85 Bài tập về chia đa thức cho đơn thức (có đáp án 2024) - Toán 8

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8

Nội dung bài viết