50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử (có đáp án năm 2024) - Toán 8

Bài giảng Toán 8 Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử

Lý thuyết

Khái niệm: Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

- Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử là cách nhóm các hạng tử phù hợp nhằm xuất hiện nhân tử chung hoặc sẻ dụng các hằng đẳng thức.

- Ta vận dụng phương pháp nhóm hạng tử khi không thể phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung hay bằng phương pháp dùng hằng đẳng thức.

Ví dụ: Phân tích đa thức x² – 4x + xy – 4y  thành nhân tử.

Hướng dẫn giải

x² – 4x + xy – 4y 

= (x² – 4x) + (xy – 4y) 

= x(x – 4) + y(x – 4)

= (x – 4)(x + y)

Chú ý:

Đối với một đa thức ta có thể có nhiều cách nhóm các hạng tử một cách thích hợp.

Khi phân tích đa thức thành nhân tử ta phải phân tích đến cuối cùng (đến khi nào không thể còn phân tích được nữa)

Dù phân tích bằng cách nào thì kết quả cũng là duy nhất.

Khi nhóm các hạng tử thì phải chú ý dấu của đa thức.

Các dạng bài tập phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử

Dạng 1: Phân tích đa thức thành nhân tử

1. Phương pháp giải

Nhóm các hạng tử một cách hợp lí để xuất hiện nhân tử chung hoặc xuất hiện các hằng đẳng thức.

- Áp dụng tính chất giao hoán, kết hợp của phép cộng các đa thức, ta kết hợp những hạng tử của đa thức thành từng nhóm thích hợp rồi dùng các phương pháp khác phân tích đa thức thành nhân tử theo từng nhóm nhỏ cuối cùng rồi phân tích chung đối với các nhóm.

Chú ý: Quy tắc dấu ngoặc

- Khi bỏ dấu ngoặc có dấu "−" đứng trước, ta phải đối dấu tất cả các số hạng trong dấu ngoặc: dấu "−“ thành dấu "+" và dấu "+” thành dấu "−". Khi bỏ dấu ngoặc có dấu "+" đứng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên.

2. Bài tập minh họa

Ví dụ 1: Phân tích các đa thức sau đây thành nhân tử:

a) 

b) 

c) 

Hướng dẫn giải

a)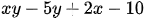 

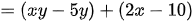
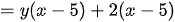
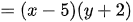
b)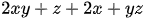 

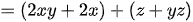
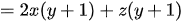
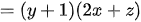
c)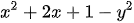 

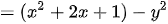
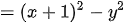
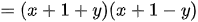
Ví dụ 2: Phân tích các đa thức sau thành nhân tử:

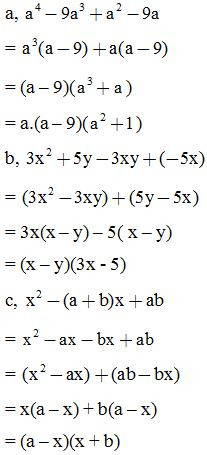
Dạng 2: Các bài toán liên quan

1. Phương pháp giải

Nhóm các hạng tử một cách hợp lí để xuất hiện nhân tử chung hoặc xuất hiện các hằng đẳng thức sau đó áp dụng để tính nhanh, tính giá trị biểu thức hoặc tìm x,….

2. Bài tập minh họa

Ví dụ 1: Tính nhanh:

Ví dụ 2: Tìm x:

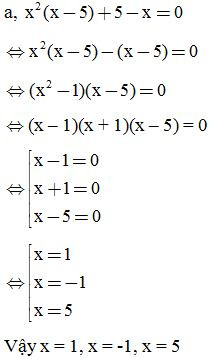
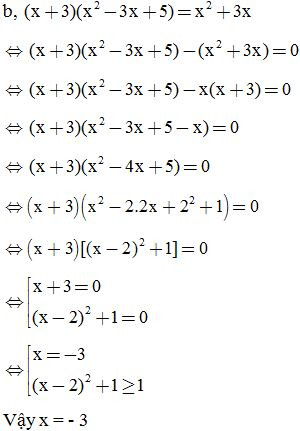
c)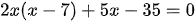 

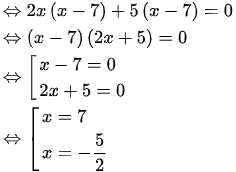
Vậy các giá trị x cần tìm là: .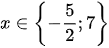

d)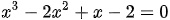 

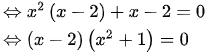
Do 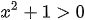 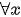 nên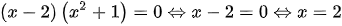 

Vậy các giá trị 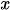 cần tìm là: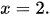 

Ví dụ 3: Tìm các số nguyên x, y thỏa mãn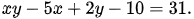 

Hướng dẫn giải

Ta có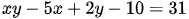 

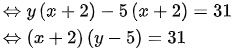
Vì x, y nguyên nên 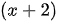 và 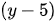 cũng nguyên và là ước của 31.

Mà 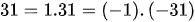. Khi đó ta xét các trường hợp:

TH1: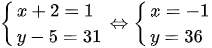 

TH2: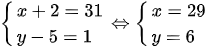 

TH3: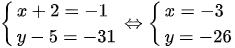 

TH4: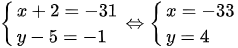 

Vậy có 4 cặp số nguyên 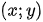  thỏa mãn yêu cầu đề bài là:

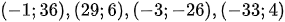
Ví dụ 4: Tính nhanh giá trị của mỗi đa thức:

a, x² – 2xy – 4z² + y2 với x = 6; y = -4; z= 45

b, 3(x – 3)(x + 7) + (x – 4)² + 48 với x = 0,5

Hướng dẫn giải

a, x² – 2xy – 4z² + y² = (x² – 2xy + y²) – 4z²

= (x – y)² – (2z)² = (x – y + 2z)(x – y – 2z)

Thay x = 6; y = -4; z= 45 vào biểu thức ta được:

(6 + 4 + 90)(6 + 4 – 90) = 100.(-80) = -8000

b, 3(x – 3)(x + 7) + (x – 4)² + 48

= 3(x² + 7x – 3x – 21) + x² – 8x + 16 + 48

= 3x² + 12x – 63 + x² – 8x + 64 = 4x² + 4x + 1 = (2x + 1)²

Thay x = 0,5 vào biểu thức ta được:

(2.0,5 + 1)² = (1 + 1)² = 4

Dạng 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức dạng ax2 + bx + c

1. Phương pháp giải

Tách hạng tử c thành tổng $c_1+c_2$ sao cho $a{x}^2+bx+c_1$ tạo thành bình phương của một tổng hoặc bình phương của một hiệu rồi đánh giá.

2. Bài tập minh họa

Ví dụ 1: Tìm GTNN của biểu thức:

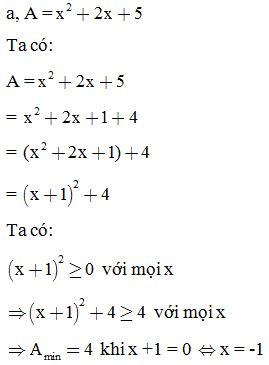
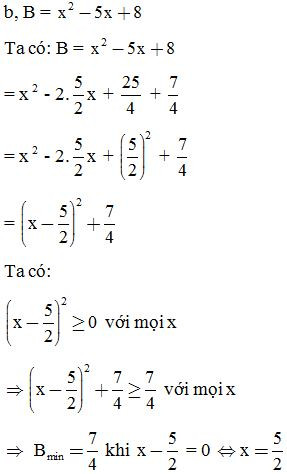
Bài tập phân tích đa thức thành nhân tử

Bài tập 1: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử:

a. 

b. 

c. 

d. 

e. 

f.

g.

h.

Hướng dẫn giải

a. Ta có:

b. Ta có:

c. Ta có:

d. Ta có:

e. Ta có:

f. Ta có:

g. Ta có:

h. Ta có:

Bài tập 2: Phân tích các đa thức sau thành nhân tử:

a) x² + y² – z² + 2xy – 2z - 1

b) x² – y² + z² – 2xz + 2y - 1

c) x⁶ – 2x⁴ – x3y3 + 2xy3

d) (x + y + z)(xy + yz + zx) - xyz

e) x² + 2xy + y² – x – y - 12

f) x²y + xy² + yz² + x²z + y²z + 2xyz

Hướng dẫn giải

a) x² + y² – z² + 2xy – 2z – 1

= (x² + 2xy + y²) + (– z² – 2z – 1)

= (x² + 2xy + y²) - ( z² + 2z + 1)

= (x + y)² – (z + 1)²

= (x + y + z + 1)(x + y – z – 1)

b) x² – y² + z² – 2xz + 2y – 1

= (x² + z² – 2xz) + (– y²+ 2y – 1)

= (x² + z² – 2xz) - (y² - 2y + 1)

= (x – z)² – (y – 1)²

= (x – z + y – 1)(x – z – y + 1)

c) x⁶ – 2x⁴ – x³y³ + 2xy³

= x(x⁵ – 2x³ – x²y³ + 2y³)

= x[x³(x² – 2) – y³(x² – 2)

= x(x³ – y³)(x² – 2)

= x(x – y)(x² – 2)(x² + xy + y²)

d) (x + y + z)(xy + yz + zx) – xyz

= x²y + xyz + x²z + xy² + y²z + xyz + yz² + xz² – xyz

= (x²y + xy²+ xyz) + (y²z + yz² + xyz) + x²z + zx²

= xy(x + y + z) + yz (x + y+ z) + xz(x + z)

= y(x+ +y + z)(x + z) + zx(x + z)

= (x + z)(xy + y² + yz + xz) = (x + z)(y+x)(x+y)

e) x² + 2xy + y² – x – y – 12

= (x + y)² – (x – y) – 12

= (x + y + 3)(x + y + 4)

f) x²y + xy² + yz² + x²z + y²z + 2xyz

= xy(x + y) + z²(x + y)²

= (x + y)(xy + z² + xz + yz)

= (x + y)(y + z)(z + x)

Bài tập 3: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử:

a. 

b. 

c. 

d. 

e. 

f. 

g. 

h. 

Bài tập 4: Phân tích đa thức thành nhân tử (bằng phương pháp nhóm hạng tử)

a. 

b. 

c. 

d. 

e. 

Bài tập 5: Phân tích đa thức sau thành nhân tử:

a. 

b. 

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

75 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung (có đáp án năm 2024)

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức (có đáp án năm 2024)

50 Bài tập về phân tích đa thức thành nhân tử bằng phương pháp nhóm các hạng tử (có đáp án năm 2024)

50 Bài tập phân tích đa thức thành nhân tử bằng các phối hợp nhiều phương pháp (có đáp án năm 2024)

50 bài tập về các phương pháp phân tích đa thức thành nhân tử (có đáp án 2024)