50 Bài tập Cộng hai số thập phân. Tổng nhiều số thập phân (có đáp án năm 2024) - Toán lớp 5

Cộng hai số thập phân. Tổng nhiều số thập phân

Kiến thức cần nhớ 

1. Cộng hai số thập phân

Quy tắc: Muốn cộng hai số thập phân ta làm như sau:

- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.

- Cộng như cộng các số tự nhiên.

- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.

Ví dụ: Đặt tính rồi tính:

a) 2,45 + 1,72

b) 19,5 + 8,75

Cách giải:

Ta đặt tính và thực hiện tính như sau:

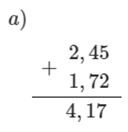
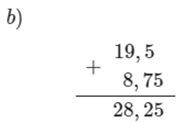
2. Tổng nhiều số thập phân

Để tính tổng nhiều số thập phân ta làm tương tự như tính tổng hai số thập phân.

Ví dụ: Đặt tính rồi tính: 23,4 + 46,83 + 15

Cách giải:

Ta đặt tính và thực hiện tính như sau:

3. Tính chất của phép cộng số thập phân

+) Tính chất giao hoán: Khi đổi chỗ hai số hạng trongg một tổng thì tổng không thay đổi.

a + b = b + a

Ví dụ: Đặt tính rồi tính ta có:

4,5 + 13,28 = 17,78

13,28 + 4,5 = 17,78

Vậy 4,5 + 13,28 = 13,28 + 4,5.

+) Tính chất kết hợp: Khi cộng một tổng hai số với số thứ ba thì ta có thể cộng số thứ nhất với tổng của hai số còn lại.

(a + b) + c = a + (b + c)

Ví dụ : 

(2,3 + 6,4) + 5,7 = 8,7 + 5,7 = 14,4

2,3 + (6,4 + 5,7) = 2,3 + 12,1 = 14,4

Vậy (2,3 + 6,4) + 5,7 = 2,3 + (6,4 + 5,7).

+) Cộng với số 0: Số thập phân nào cộng với 0 cũng bằng chính số thập phân đó.

Ví dụ: 1,5 + 0 = 1,5.

Lưu ý: Ta thường áp dụng các tính chất của phép cộng số thập phân trong các bài tính nhanh.

Bài tập tự luyện (có đáp án) 

Bài 1: Tính:

a) $5,27+14,35+9,25$ ;                        b) $6,4+18,36+52$ ;

c) $20,08+32,91+7,15$ ;                      d) $0,75+0,09+0,8$ .

Hướng dẫn giải 

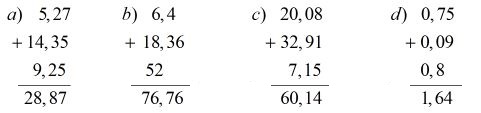
Bài 2: Tính rồi so sánh giá trị của $(a+b)+c$ và $a+(b+c)$:

Nhận xét: Phép cộng các số thập phân có tính chất kết hợp:

Khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của hai số còn lại.

$(a+b)+c=a+(b+c)$

Hướng dẫn giải 

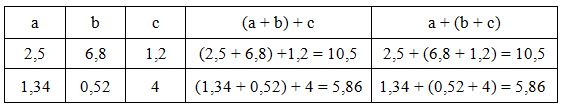
Nhận xét: $(a+b)+c=a+(b+c).$

Bài 3: Sử dụng tính chất giao hoán và tính chất kết hợp để tính:

a) $12,7+5,89+1,3;$

b) $38,6+2,09+7,91;$

c) $5,75+7,8+4,25+1,2;$

d) $7,34+0,45+2,66+0,55.$

Hướng dẫn giải 

a) $12,7+5,89+1,3$

    $=(12,7+1,3)+5,89$

    $=14+5,89$

    $=19,89$

b) $38,6+2,09+7,91$

    $=38,6+(2,09+7,91)$

    $=38,6+10$

    $=48,6$

c) $5,75+7,8+4,25+1,2$

    $=(5,75+4,25)+(7,8+1,2)$

    $=10+9$

    $=19$

d) $7,34+0,45+2,66+0,55$

   $=(7,34+2,66)+(0,45+0,55)$

   $=10+1$

   $=11$

Xem thêm các dạng bài tập khác:

50 Bài tập Số thập phân bằng nhau. So sánh hai số thập phân (có đáp án năm 2023)

50 Bài tập Hàng của số thập phân, đọc viết số thập phân (có đáp án năm 2023)

50 Bài tập Cộng hai số thập phân. Tổng nhiều số thập phân (có đáp án năm 2023)

50 Bài tập Nhân một số thập phân với một số thập phân (có đáp án năm 2023)

50 Bài tập Chia một số thập phân cho một số thập phân (có đáp án năm 2023)