50 Bài tập Bảng căn bậc hai (có đáp án năm 2024) - Toán 9

Bảng căn bậc hai

Kiến thức cần nhớ 

1. Giới thiệu bảng căn bậc hai

+ Bảng được chia thành các hàng và các cột.

+ Căn bậc hai của các số được viết bởi không qua ba chữ số từ 1,00 đến 99,9 được ghi sẵn trong bảng ở các cột từ cột 0 đến cột 9.

+ Tiếp đó là chín cột hiệu chính được dùng để hiệu chính chữ số cuối của căn bậc hai của các số được viết bởi bốn chữ số từ 1,000 đến 99,99.

+ Bảng căn bậc hai.

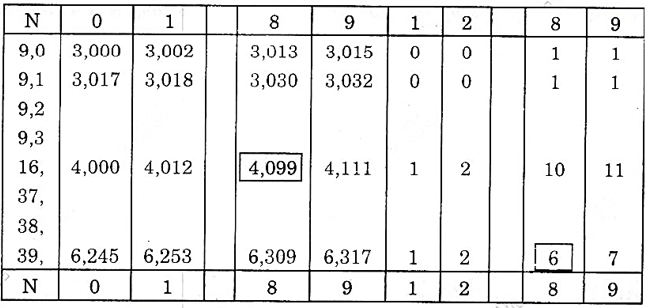
2. Cách dùng bảng

a) Tìm căn bậc hai của số lớn hơn 1 và nhỏ hơn 100

Ví dụ 1. Tìm $\sqrt{\mathrm{1,68}}$.

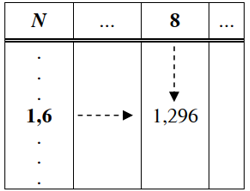
Tại giao của hàng 1,6 và cột 8, ta thấy số 1,296.

Vậy $\sqrt{\mathrm{1,68}}\approx \mathrm{1,269}$.

Ví dụ 2. Tìm $\sqrt{\mathrm{39,18}}$.

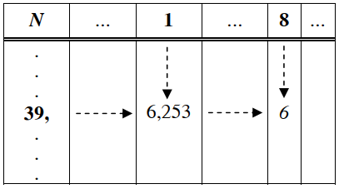
Tại giao của hàng 39 và cột 1, ta thấy số 6,253.

Ta có: $\sqrt{\mathrm{39,1}}\approx \mathrm{6,253}$.

Tại giao của hàng 39 và cột 8 hiệu chính, ta thấy số 6.

Ta dùng số 6 này để hiệu chính chữ số cuối ở số 6,253 như sau:

6,253 + 0,006 = 6,259.

Vậy $\sqrt{\mathrm{39,18}}\approx \mathrm{6,259}$.

b) Tìm căn bậc hai của số lớn hơn 100

Ví dụ 3. Tìm $\sqrt{998}$.

Ta có:

$$\begin{gathered} \sqrt{998}=\sqrt{\mathrm{9,88}.100} \\ =10.\sqrt{\mathrm{9,88}} \end{gathered}$$

≈ 10 . 3,143 = 31,43.

Vậy $\sqrt{998}\approx \mathrm{31,43}$.

c) Tìm căn bậc hai của số không âm và nhỏ hơn 1

Chú ý. Để thực hành nhanh, khi tìm căn bậc hai của số không âm lớn hơn 100 hoặc nhỏ hơn 1, ta dùng hướng dẫn của bảng: “Khi dời dấu phẩy trong số N đi 2, 4, 6, …chữ số thì dời dấu phẩy trong số N đi 1, 2, 3, …chữ số”.

Ví dụ 4.Tìm $\sqrt{\mathrm{0,678}}$.

Ta có

$$\begin{gathered} \sqrt{\mathrm{0,678}}=\sqrt{\mathrm{67,8}:100} \\ =\sqrt{\mathrm{67,8}}:\sqrt{100} \end{gathered}$$

≈ 8,234 : 10 = 0,8234.

Bài tập tự luyện (có đáp án)

Bài 1: Tìm:

a)  

b) 

Hướng dẫn giải

Bài 2: Tìm:

b) 

Hướng dẫn giải

Bài 3: Dùng bảng căn bậc hai, tìm giá trị gần đúng của nghiệm phương trình: x²=0,3982

Hướng dẫn giải

Bài 4: Dùng bảng số để tìm căn bậc hai số học của mỗi số sau đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

Hướng dẫn giải

Sử dụng máy tính cho kết quả như sau:

So sánh kết quả, ta thấy:

Bài 5: Dùng bảng số để tìm căn bậc hai số học của mỗi số sau đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

115; 232; 571; 9691.

Hướng dẫn giải

Sử dụng máy tính cho kết quả như sau:

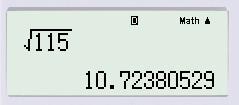
So sánh kết quả, ta được:

Bài 6: Dùng bảng số để tìm căn bậc hai số học của mỗi số sau đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

 ; 

Hướng dẫn giải

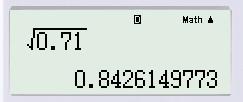
So sánh các số như sau:

Vì 

Nhận thấy rằng, đối với các số từ 0 đến 1, lấy căn bậc hai ta luôn tìm được kết quả lớn hơn số ban đầu!

Bài 7: Biết  Hãy tính:

Hướng dẫn giải

Ta có:

+ 

+ 

(vì 9,1190 = 9,119)

+ 

Bài 8: Dùng bảng căn bậc hai để tìm giá trị gần đúng của nghiệm mỗi phương trình sau:

a) 

b) 

Hướng dẫn giải

a) 

b) 

Xem thêm các dạng Toán khác :

50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2023)

50 Bài tập Bảng căn bậc hai (có đáp án năm 2023)

50 Bài tập Biến đổi đơn giản biểu thức căn thức bậc hai (có đáp án năm 2023)

50 Bài tập Rút gọn biểu thức chứa căn thức bậc hai (có đáp án năm 2023)

50 Bài tập Căn bậc hai (có đáp án năm 2023)