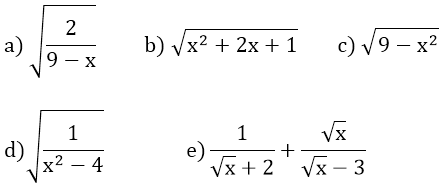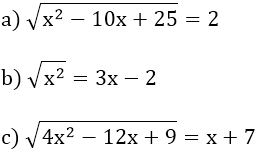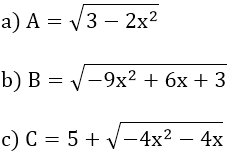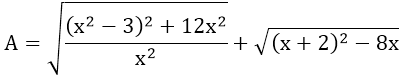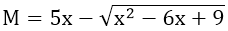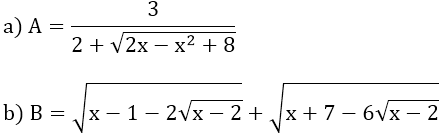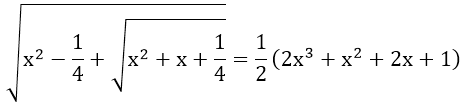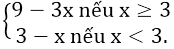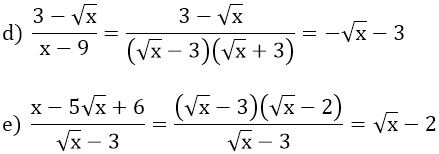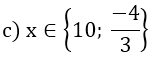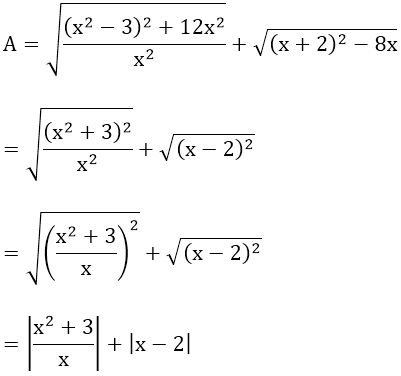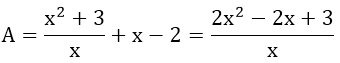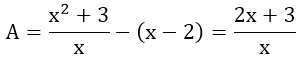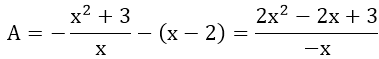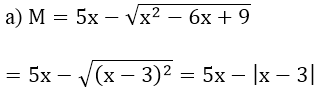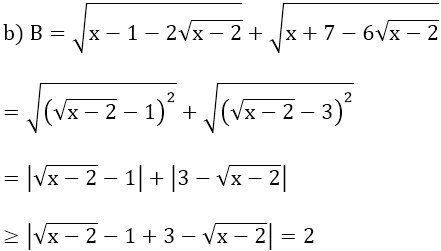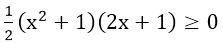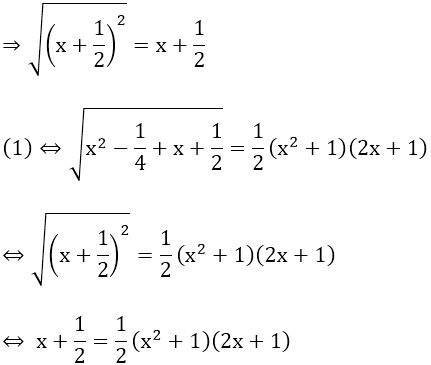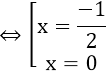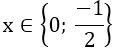50 Bài tập Căn bậc hai (có đáp án năm 2024) - Toán 9

Căn bậc hai

Kiến thức cần nhớ 

1. Căn bậc hai

a. Khái niệm: Căn bậc hai của một số a không âm là số x sao cho x² = a.

Ví dụ 1. Số 16 là số không âm, căn bậc hai của 16 là số x sao cho x² = 16.

Do đó căn bậc hai của 16 là 4 và −4.

b. Tính chất:

- Số âm không có căn bậc hai.

- Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết $\sqrt{0}=0$.

- Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là $\sqrt{a}$ , số âm ký hiệu là $-\sqrt{a}$.

Ví dụ 2.

- Số −12 là số âm nên không có căn bậc hai.

- Số 64 có hai căn bậc hai là 8 và −8.

- Số 15 có hai căn bậc hai là $\sqrt{15}$ và $-\sqrt{15}$ .

2. Căn bậc hai số học

a. Định nghĩa: Với số dương a, số $\sqrt{a}$ được gọi là căn bậc hai số học của a. Số 0 cũng được gọi là căn bậc hai số học của 0.

Ví dụ 3. Căn bậc hai số học của 36 là $\sqrt{36}$ (= 4).

- Căn bậc hai số học của 7 là $\sqrt{7}$.

Chú ý. Với a ≥ 0, ta có:

Nếu $x=\sqrt{a}$ thì x ≥ 0 và x² = a;

Nếu x ≥ 0 và x² = a thì $x=\sqrt{a}$.

- Ta viết $x=\sqrt{a}\iff \left\{\begin{array}{l}x\ge \mathrm{0,}\\ x^2=a.\end{array}\right.$

Ví dụ 4. Tìm căn bậc hai số học của các số sau đây: 25; 81; 225; 324.

Lời giải:

Ta có:

•  $\sqrt{25}=5$ vì 5 > 0 và 5² = 25;

•  $\sqrt{81}=9$ vì 9 > 0 và 9² = 81;

•  $\sqrt{225}=15$ vì 15 > 0 và 15² = 225;

•  $\sqrt{324}=18$ vì 18 > 0 và 18² = 324.

b. Phép khai phương:

- Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương).

- Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.

Ví dụ 5. 

- Căn bậc hai số học của 9 là 3 nên 9 có hai căn bậc hai là 3 và −3.

- Căn bậc hai số học cuả 256 là 16 nên 256 có hai căn bậc hai là 16 và −16.

3. So sánh các căn bậc hai số học

Định lí. Với hai số a và b không âm, ta có: $a<b\iff \sqrt{a}<\sqrt{b}$.

Ví dụ 6. So sánh:

a) 3 và $\sqrt{11}$;

b) 5 và $\sqrt{15}$.

Lời giải:

a) Vì 9 < 11 nên $\sqrt{9}<\sqrt{11}$.

Vậy $3<\sqrt{11}$.

b) Vì 25 > 15 nên $\sqrt{25}>\sqrt{15}$.

Vậy $5>\sqrt{15}$.

Bài tập tự luyện (có đáp án)

Bài 1: Tìm x để các căn thức bậc hai sau có nghĩa

Bài 2: Rút gọn các biểu thức sau:

Bài 3: Giải các phương trình sau:

Bài 4: Chứng minh rằng:

    √2 + √6 + √12 + √20 + √30 + √42 < 24

Bài 5: Tìm giá trị lớn nhất của biểu thức:

Bài 6: Rút gọn biểu thức A

Bài 7: Cho biểu thức 

    a) Rút gọn biểu thức M;

    b) Tìm các giá trị của x để M = 4.

Bài 8: Tìm giá trị nhỏ nhất của mỗi biểu thức:

Bài 9: Tìm x, để

Đáp án và hướng dẫn giải

Bài 1:

    a) x < 9         b) x ∈ R         c)-3 ≤ x ≤ 3

Bài 2:

    a) √10 - 3         b) √5 - 2

    c) 6 - 2x - |x - 3|= 

Bài 3:

    a) x = 3 hoặc x = 7

    b) x = 1

Bài 4:

    √2 + √6 + √12 + √20 + √30 + √42 < √2,25 + √6,25 + √12,25 + √20,25 + √30,25 + √42,25 = 24

Bài 5:

    a) Giá trị lớn nhất của A là √3 khi x = 0

    b) Giá trị lớn nhất của B là 2 khi x = 1/3

    c) Giá trị lớn nhất của C là 6 khi x = -1/2

Bài 6:

    ĐKXĐ: x ≠ 0

    Với x ≥ 2, A trở thành:

    Với 0 < x < 2, A trở thành:

    Với x < 0, A trở thành:

    Vậy

Bài 7:

    Nếu x ≥ 3 thì M = 5x - (x - 3) = 4x + 3

    Nếu x < 3 thì M = 5x + (x - 3) = 6x - 3

    b) Ta xét 2 trường hợp

        + M = 4 ⇔ 4x + 3 = 4 ⇔ x = 1/4 (không thỏa mãn x ≥ 3)

        + M = 4 ⇔ 6x - 3 = 4 ⇔ x = 7/6 (thỏa mãn x < 3)

Bài 8:

    a) Giá trị nhỏ nhất của A = 3/5 khi x = 1

    Vậy Giá trị nhỏ nhất của B là 2, đạt được khi 

    ⇔ 3 ≤ x ≤ 11

Bài 9:

    Vì vế trái không âm nên vế phải 

    Do x² + 1 > 0 ∀x ∈ R nên 2x + 1 ≥ 0 ⇔ x ≥ -1/2

    ⇔ 2x + 1 = (x² + 1)(2x + 1)

    ⇔ (2x + 1)[1 -(x² + 1)] = 0

    Vậy 

Xem thêm các dạng Toán khác :

50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2023)

50 Bài tập Bảng căn bậc hai (có đáp án năm 2023)

50 Bài tập Biến đổi đơn giản biểu thức căn thức bậc hai (có đáp án năm 2023)

50 Bài tập Rút gọn biểu thức chứa căn thức bậc hai (có đáp án năm 2023)

50 Bài tập Căn bậc hai (có đáp án năm 2023)