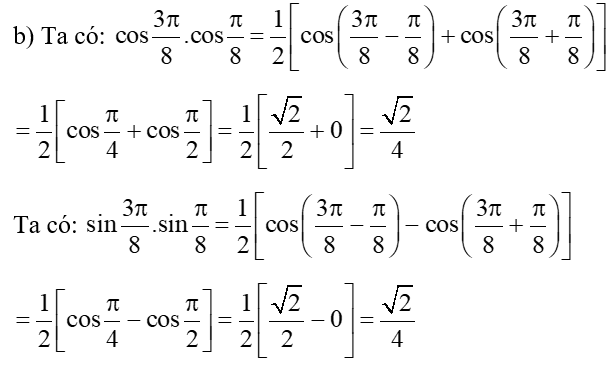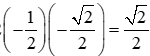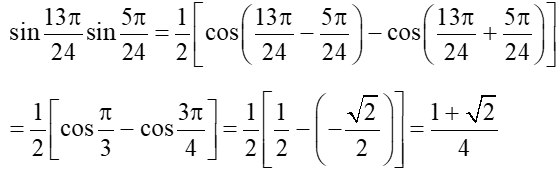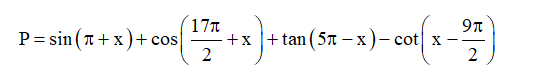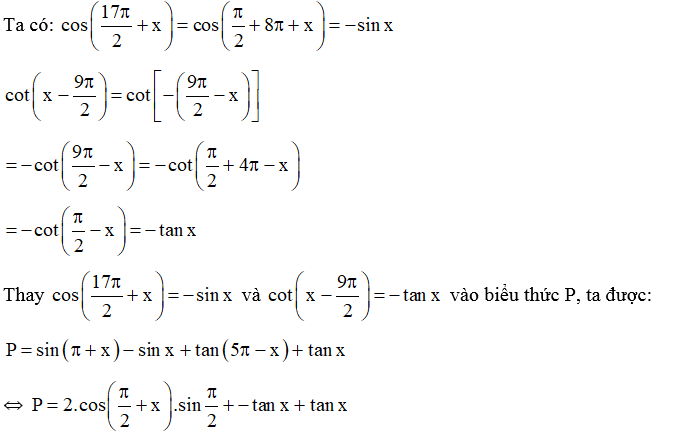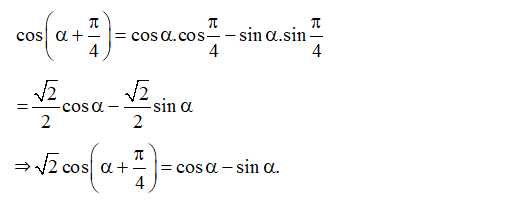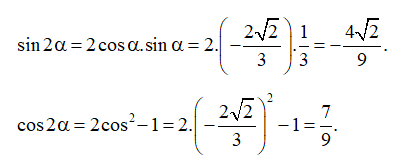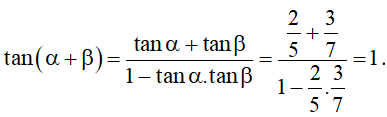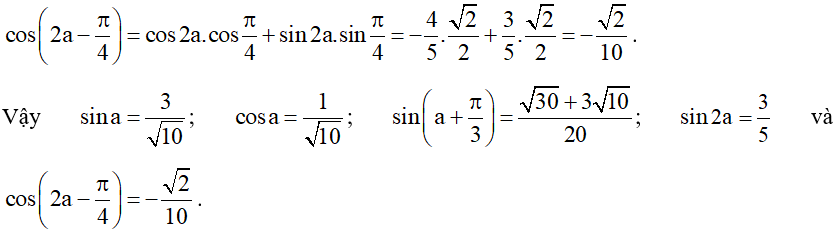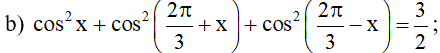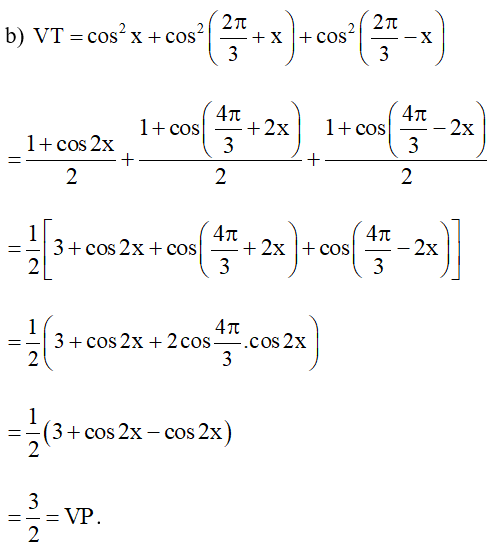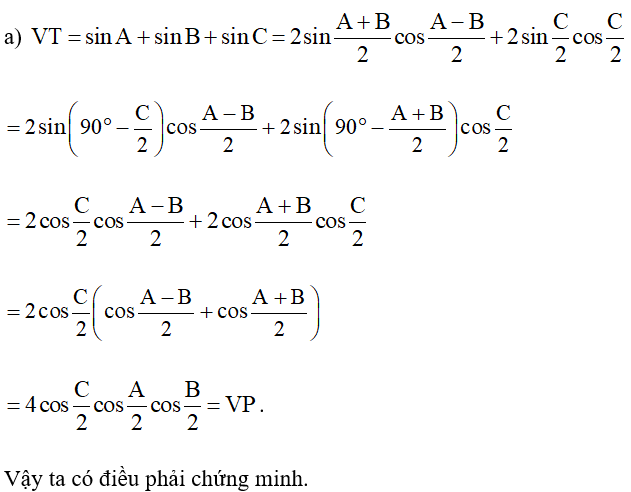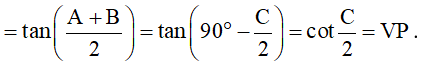Bài tập về công thức lượng
I. Lý thuyết
1. Bảng công thức lượng giác dành cho lớp 10 - 11 - 12
Công thức Lượng giác cơ bản
| tan x = |
cot x = |
|
sin2x + cos2x = 1 |
tan x . cot x = 1 |
|
1 + tan2 x = |
1 + cot2 x = |
Thơ nhớ hàm lượng giác cơ bản
Sin bình cộng cos bình thì phải bằng 1
Sin bình thì bằng tan bình trên tan bình cộng 1
Cos bình bằng một trên một cộng tan bình
Một trên sin bình bằng 1 cộng cot bình
Một trên cos bình bằng một cộng tan bình
Bắt được quả tan,
Sin nằm trên cos,
Cot cải lại,
Cos nằm trên sin.
Hoặc là:
Bắt được quả tan,
Sin nằm trên cos (tan x = sin x / cos x),
Cot dại dột,
Bị cos đè cho (cot x = cos x / sin x).
Công thức cộng lượng giác
| cos(a + b) = cos a.cos b - sin a.sin b | cos(a - b) = cos a.cos b + sin a.sin b |
| sin(a + b) = sin a.cos b + sin b.cos a | sin(a - b) = sin a.cos b - sin b.cos a |
| tan(a + b) = |
tan(a - b) = |
Thơ công thức cộng
Cos cộng cos thì bằng hai cos cos
Cos trừ cos phải bằng trừ hai sin sin
Sin cộng sin thì bằng hai sin cos
Sin trừ sin bằng hai cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin nhớ nha dấu trừ
Tan tổng thì lấy tổng tan
Chia một trừ với tích tan, dễ mà.
Công thức các cung liên kết trên đường tròn lượng giác
|
Góc đối nhau ( cos đối) |
Góc bù nhau (sin bù) |
Góc phụ nhau (Phụ chéo) |
Góc hơn kém (Khác pi tan) |
| cos (-α) = cos α | sin (π - α) = sin α | sin (π/2 - α)= cos α | sin (π + α) = - sin α |
| sin (-α) = -sin α | cos (π - α) = - cos α | cos (π/2 - α) = sinα | cos (π + α) = - cosα |
| tan (-α) = - tan α | tan ( π - α) = - tan α | tan (π/2 - α) = cot α | tan (π + α) = tanα |
| cot (-α) = -cot α | cot (π - α) = – cot α | cot (π/2 - α) = tan α | cot (π + α) = cotα |
Cung hơn kém π / 2
- cos(π/2 + x) = - sinx
- sin(π/2 + x) = cosx
Thơ nhớ cung đặc biệt
Cos đối, sin bù, phụ chéo, khác pi tan.
Cosin của 2 góc đối thì bằng nhau.
Sin của 2 góc bù nhau cũng bằng nhau.
Phụ chéo là 2 góc phụ nhau thì sin góc này bằng cos góc kia.
Tan góc này bằng Cot góc kia.
Tan của 2 góc hơn kém pi cũng bằng nhau.
2. Cách học thuộc bảng công thức lượng giác nhanh chóng
Cách học thuộc các công thức lượng giác bằng thơ
Công thức CỘNG trong lượng giác
Cos + cos = 2 cos cos
cos trừ cos = trừ 2 sin sin
Sin + sin = 2 sin cos
sin trừ sin = 2 cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin “coi chừng” (dấu trừ).
Tan tổng thì lấy tổng tan
Chia một trừ với tích tan, dễ òm.
HÀM SỐ LƯỢNG GIÁC
Bắt được quả tan
Sin nằm trên cos (tan@ = sin@:cos@)
Cot dại dột
Bị cos đè cho. (cot@ = cos@:sin@)
Cách 2:
Bắt được quả tan
Sin nằm trên cos
Cot cãi lại
Cos nằm trên sin!
GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG ĐẶC BIỆT
Cos đối, sin bù, phụ chéo, khác pi tan
Cosin của 2 góc đối bằng nhau; sin của 2 góc bù nhau thì bằng nhau; phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tan góc này = cot góc kia; tan của 2 góc hơn kém pi thì bằng nhau.
CÔNG THỨC LƯỢNG GIÁC NHÂN BA
Nhân ba một góc bất kỳ,
sin thì ba bốn, cos thì bốn ba,
dấu trừ đặt giữa 2 ta, lập phương chỗ bốn,
… thế là ok.
Công thức gấp đôi:
+ Sin gấp đôi = 2 sin cos
+ Cos gấp đôi = bình cos trừ bình sin
= trừ 1 + 2 lần bình cos
= + 1 trừ 2 lần bình sin
+Tang gấp đôi
Tan đôi ta lấy đôi tan (2 tan)
Chia 1 trừ lại bình tan, ra liền.
Cách nhớ công thức: tan(a + b)=(tana + tanb)/1 - tana.tanb
tan một tổng 2 tầng cao rộng
trên thượng tầng tan + tan tan
dưới hạ tầng số 1 ngang tàng
dám trừ một tích tan tan oai hùng
CÔNG THỨC LƯỢNG GIÁC BIẾN ĐỔI TÍCH THÀNH TỔNG
Cos cos nửa cos(+) cộng cos(-)
Sin sin nửa cos(-) trừ cos (+)
Sin cos nửa sin(+) cộng sin(-)
CÔNG THỨC LƯỢNG GIÁC BIẾN ĐỔI TỔNG THÀNH TÍCH
sin tổng lập tổng sin cô
cô tổng lập hiệu đôi cô đôi chàng
còn tan tử cộng đôi tan (hoặc là: tan tổng lập tổng 2 tan)
một trừ tan tích mẫu mang thương sầu
gặp hiệu ta chớ lo âu,
đổi trừ thành cộng ghi sâu vào lòng
Một phiên bản khác của câu Tan mình cộng với tan ta, bằng sin 2 đứa trên cos ta cos mình… là
tanx cộng tany: tình mình cộng lại tình ta, sinh ra 2 đứa con mình con ta
tanx trù tan y: tình mình hiệu với tình ta sinh ra hiệu chúng, con ta con mình
CÔNG THỨC CHIA ĐÔI (tính theo t = tg(a/2))
Sin, cos mẫu giống nhau chả khác
Ai cũng là một cộng bình tê (1 + t2)
Sin thì tử có hai tê (2t),
cos thì tử có một trừ bình tê (1 - t2).
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Sao Đi Học (Sin = Đối / Huyền)
Cứ Khóc Hoài (Cos = Kề / Huyền)
Thôi Đừng Khóc (Tan = Đối / Kề)
Có Kẹo Đây (Cot = Kề/ Đối)
Sin: đi học (cạnh đối - cạnh huyền)
Cos: không hư (cạnh đối - cạnh huyền)
Tan: đoàn kết (cạnh đối - cạnh kề)
Cot: kết đoàn (cạnh kề - cạnh đối)
Tìm sin lấy đối chia huyền
Cos lấy cạnh kề, huyền chia nhau
Còn tan ta hãy tính sau
Đối trên, kề dưới chia nhau ra liền
Cot cũng dễ ăn tiền
Kề trên, đối dưới chia liền là ra
Sin bù, cos đối, hơn kém pi tan, phụ chéo.
+ Sin bù: Sin(180-a) = sina
+ Cos đối: Cos(-a)=cosa
+ Hơn kém pi tang:
Tan (a + 180) = tan a
Cot (a + 180) = cot a
+ Phụ chéo là 2 góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Công thức tổng quát hơn về việc hơn kém pi như sau:
Hơn kém bội 2 pi sin, cos
Tan, cot hơn kém bội pi.
Sin(a+k.2.1800) = sin a ; Cos(a + k.2.1800) = cos a
Tan (a + k1800)=tan a ; Cot(a + k1800)=cot a
* sin bình + cos bình = 1
* Sin bình = tan bình trên tan bình + 1.
* cos bình = 1 trên 1 + tan bình.
* Một trên cos bình = 1 + tan bình.
* Một trên sin bình = 1 + cot bình.
(Chú ý sin *; cos @ ; tan @ ;cot * với các dấu * và @ là chúng có liên quan nhau trong CT trên)
Học công thức lượng giác “thần chú”
• Sin = đối/ huyền
Co s= kề/ huyền
Tan = đối/ kề
Cot = kề/ huyền
* Thần chú: Sin đi học, Cos không hư, tan đoàn kết, cot kết đoàn
Hoặc: Sao đi học, cứ khóc hoài, thôi đừng khóc, có kẹo đây!
• Công thức cộng:
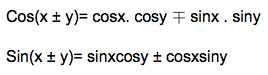
* Thần chú: Cos thì cos cos sin sin
Sin thì sin cos cos sin rõ ràng
Cos thì đổi dấu hỡi nàng
Sin thì giữ dấu xin chàng nhớ cho!
* Thần chú: Tan một tổng hai tầng cao rộng
Trên thượng tầng tan cộng cùng tan
Hạ tầng số 1 ngang tàng
Dám trừ đi cả tan tan oai hùng
Hoặc: Tan tổng thì lấy tổng tan
Chia một trừ với tích tan, dễ òm.
• Công thức biến đổi tổng thành tích:
Ví dụ: cosx + cosy= 2cos cos
(Tương tự những công thức như vậy)
* Thần chú: cos cộng cos bằng 2 cos cos
Cos trừ cos bằng trừ 2 sin sin
Sin cộng sin bằng 2 sin sin
Sin trừ sin bằng 2 cos sin.
* Tan ta cộng với tan mình bằng sin hai đứa trên cos mình cos ta.
Công thức biến đổi tích thành tổng:
Ví dụ: cosx.cosy=1/2[cos(x+y)+cos(x-y)] (Tương tự những công thức như vậy)
* Thần chú: Cos cos nửa cos(+) cộng cos(-)
Sin sin nửa cos(-) trừ cos(+)
Sin cos nửa sin(+) cộng sin(-)
• Công thức nhân đôi:
Ví dụ: sin2x= 2sinxcosx (Tương tự những công thức như vậy)
Thần chú: Sin gấp đôi bằng 2 sin cos
Cos gấp đôi bằng bình cos trừ bình sin
= trừ 1 cộng hai bình cos
= cộng 1 trừ hai bình sin
Chỉ việc nhớ công thức nhân đôi của cos bằng thần chú trên rồi từ đó có thể suy ra công thức hạ bậc.
Tan gấp đôi = Tan đôi ta lấy đôi tan (2 tan)
Chia 1 trừ lại bình tan, ra liền.
• Hàm số lượng giác và các cung có liên quan đặc biệt:
Ví dụ: Cos(-x) = cosx
Tan( + x) = tan x
* Thần chú: Sin bù, Cos đối, Tan Pi,
Phụ nhau Sin Cos, ắt thì phân chia
Hoặc: Cos đối, sin bù, phụ chéo, hơn kém pi tan.
II. Bài tập vận dụng
Bài 1. Tính sin2a và tan2a biết cos a = và
Hướng dẫn giải
Vì
Ta có:
sin2a + cos2a = 1 ⇒ sin2a = 1 – cos2a = 1 - 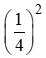
⇒ sina = .
Ta có: sin2a = 2sina cosa = 2.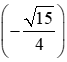
Ta có: tana =
⇒=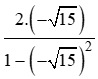
Bài 2. Tính
a) sin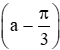
b) cos.cos + sin.sin.
Hướng dẫn giải
a) Vì 0
Ta có: sin2a + cos2a = 1 ⇒ cos2a = 1 – sin2a = 1-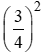
⇒ cosa = null.
Vậy sin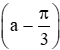
Suy ra: .
Bài 3. Tính
a) cos(–15°) + cos255°;
b) sinsin.
Hướng dẫn giải
a) Ta có:
cos(-15o) + cos255o = 2.cos.cos
= 2.cos120o.cos(135o) = 2
Vậy cos(–15°) + cos255° = .
b) Ta có:
Vậy .
Bài 4. Rút gọn biểu thức sau:
Hướng dẫn giải
⇔
Vậy P = −2sin x.
Bài 5. Chứng minh rằng:
Hướng dẫn giải
Ta có:
Bài 6. Cho và Tính các giá trị lượng giác của góc 2α.
Hướng dẫn giải
Do ⇒ cos α < 0.
Ta có:
⇒ (do cos α < 0).
Bài 7. Tính α + β biết .
Hướng dẫn giải
Áp dụng công thức cộng đối với tang, ta được:
Vậy .
Bài 8. Cho , với . Tính sina, cosa, 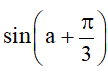
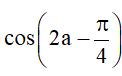
Hướng dẫn giải
Vì nên sina > 0, cosa > 0.
• Áp dụng công thức hạ bậc, ta được:
Suy ra (do sina > 0)
• Áp dụng công thức hạ bậc, ta được: .
Suy ra .
• Áp dụng công thức cộng đối với sin, ta được:
.
• Áp dụng công thức nhân đôi, ta được:
.
• Áp dụng công thức cộng đối với côsin, ta được:
Bài 9. Chứng minh rằng:
a) ;
Hướng dẫn giải
a) VT = cos3x.sinx – sin3x.cosx
= cosx.sinx.(cos2x – sin2x)
= VP.
Vậy ta có điều phải chứng minh.
Bài 10. Cho ∆ABC. Chứng minh rằng:
a) ;
b) ;
c) , với R là bán kính đường tròn ngoại tiếp ∆ABC và S là diện tích ∆ABC.
Hướng dẫn giải
∆ABC, có: , suy ra
Do đó .
b)
Vậy ta có điều phải chứng minh.
c) VT = sin2A + sin2B + sin2C
= 2sin(A + B).cos(A – B) + 2sinC.cosC
= 2sin(180° – C).cos(A – B) + 2sinC.cosC
= 2sinC.cos(A – B) + 2sinC.cosC
= 2sinC.[cos(A – B) + cosC]
= 2sinC.[cos(A – B) + cos(180° – A – B)]
= 2sinC.[cos(A – B) – cos(A + B)]
= –4sinC.sinA.sin(–B)
= 4sinA.sinB.sinC
.
Vậy ta có điều phải chứng minh.
11: Tính:
a. ;
b. .
Hướng dẫn:
a.
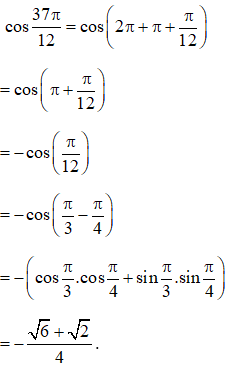
b.
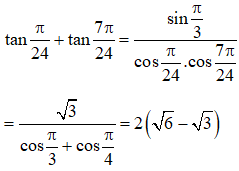
12: Tính:
a. biết với ;
b. biết , và , .
Hướng dẫn:
a. Ta có:
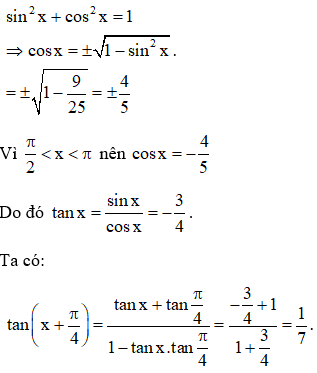
b. Ta có:
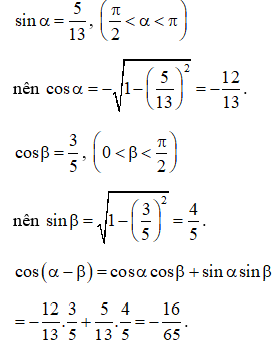
13: Chứng minh rằng:
a.
b.
Hướng dẫn:
a. (Áp dụng công thức hạ bậc) Ta có:
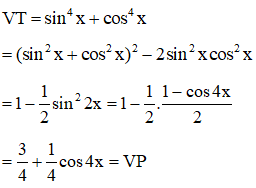
Suy ra đpcm.
b. (Áp dụng công thức góc nhân ba) Ta có:
Suy ra đpcm.
14: Cho tam giác ABC. Chứng minh rằng:
Hướng dẫn:
Do tam giác ABC có , suy ra
Do đó, ta có:
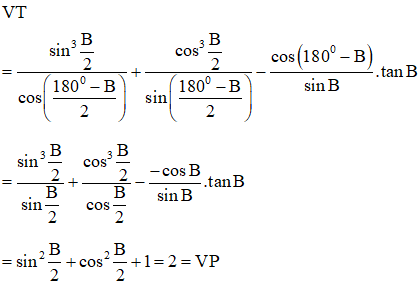
Suy ra đpcm.
15: Rút gọn biểu thức:
a.
b.
Hướng dẫn:
a. Ta có:
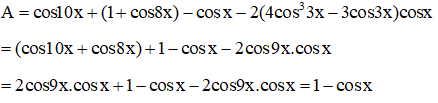
b. Ta có:
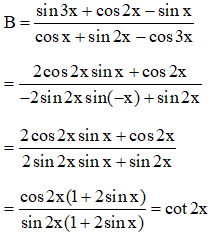
16: Rút gọn biểu thức:
Hướng dẫn:
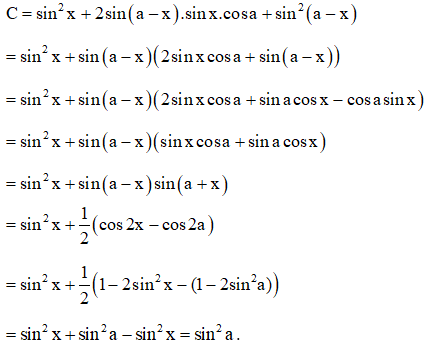
17: Chứng minh biểu thức sau không phụ thuộc vào x:
Hướng dẫn:
Ta có:
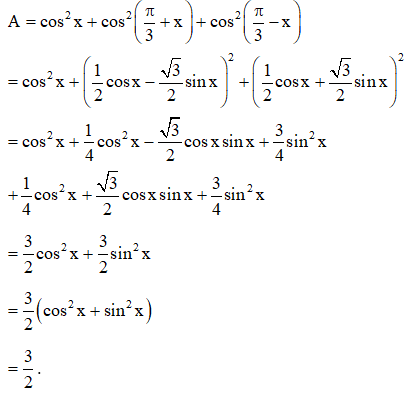
Vậy biểu thức đã cho không phụ thuộc vào x.
18: Chứng minh biểu thức sau không phụ thuộc vào x:
Hướng dẫn:
Ta có:
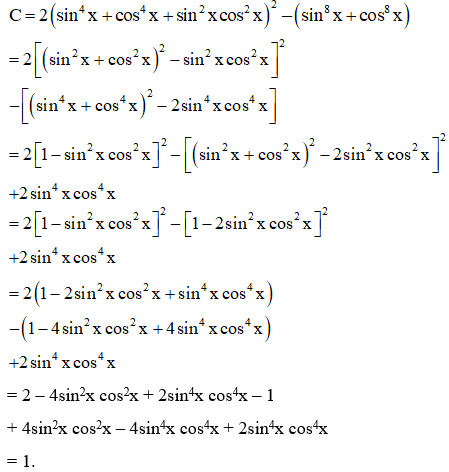
Vậy biểu thức đã cho không phụ thuộc vào x.
Xem thêm các dạng bài tập hay, có đáp án: