Kiến thức cần nhớ
1. Khái niệm tỉ số lượng giác của một góc nhọn
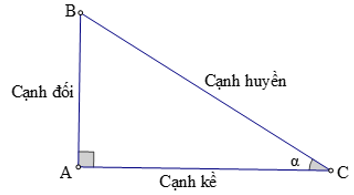
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cos α.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tan α.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cot α.
Ví dụ 1. Cho tam giác ABC có ˆC=α.
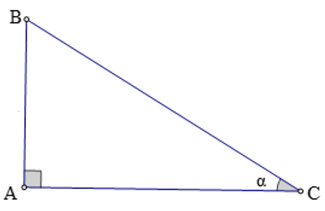
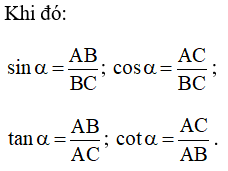
Nhận xét: Nếu α là một góc nhọn thì:
0 < sin α < 1; 0 < cos α < 1; tan α > 0; cot α > 0.
Ví dụ 2. Cho tam giác ABC có ˆC=α
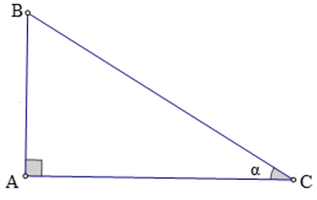
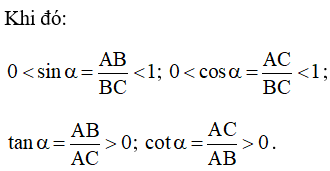
Chú ý: Nếu hai góc nhọn α và β có sin α = sin β (hoặc cos α = cos β, hoặc tan α = tan β, hoặc cot α = cot β) thì α = β vì chúng là hai góc tương ứng của hai tam giác vuông đồng dạng.
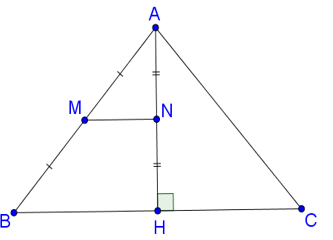
Ví dụ 3. Cho tam giác ABC có AB = AC, đường cao AH. MN là đường trung bình của tam giác ABH. Chứng minh ^AMN=ˆC.
Lời giải:
Vì AH là đường cao của ∆ABC nên AH⊥BC hay AH⊥BH (1)
Mà MN là đường trung bình của ∆AMN nên:
+ AB = 2AM; AH = 2AN.
+ MN // BH (2)
Từ (1) và (2) suy ra MN⊥BH (tính chất từ vuông góc đến song song).

2. Tỉ số lượng giác của hai góc phụ nhau
Định lí. Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Ví dụ 4. Cho tam giác ABC vuông tại A có ˆB=α; ˆC=β.
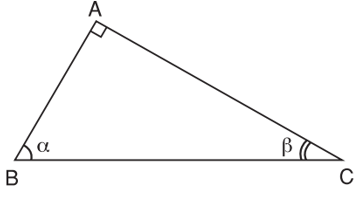
Khi đó, α + β = 90° (trong tam giác vuông hai góc nhọn phụ nhau).
Ta có: sin α = cos β; cos α = sin β; tan α = cot β; cot α = tan β.
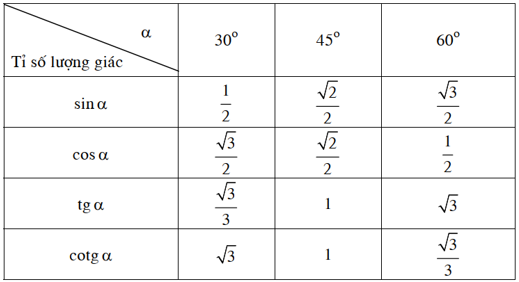
Bảng lượng giác của một số góc đặc biệt:
Ví dụ 5. Cho tam giác ABC vuông tại A có BC = 16, ˆC=30o. Tính độ dài AB.
Lời giải:
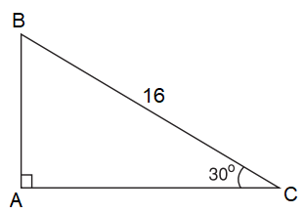
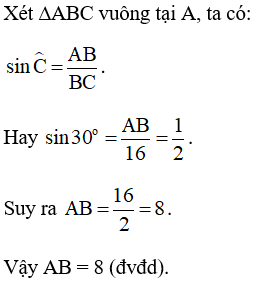
Chú ý: Từ nay khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta bỏ kí hiệu " ^ " đi.
Ví dụ 6. Góc A là góc nhọn thì ta viết sin A thay cho sinˆA.
Bài tập tự luyện
Bài 1: Xét tam giác ABC vuông tại A có ∠B = α. Chứng minh rằng
Hướng dẫn giải
a)
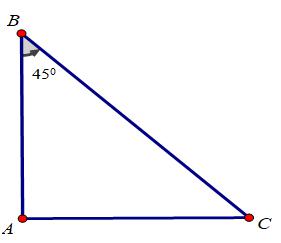
Tam giác ABC vuông tại A có ∠B = 450 ⇒ΔABC vuông cân tại A
⇒AB = AC ⇒AB/AC = 1
b)
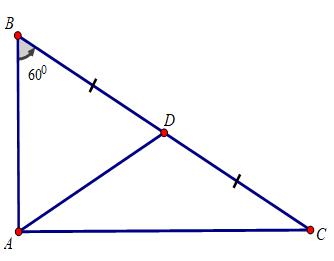
Kẻ trung tuyến AD của tam giác vuông ABC
⇒ AD = BD = BC/2
Tam giác ABD có: AD = BD, ∠(ABD) = 600
⇒ ΔABD là tam giác đều
⇒ AB = AD = BC/2 ⇒ BC = AB
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
⇔ AB2 + AC2 = 4 AB2
⇔ AC2 = 3 AB2 ⇔ AC = √3 AB
⇔ AC/AB = √3
Bài 2: Cho tam giác ABC vuông tại A có ∠C = β. Hãy viết các tỉ số lượng giác của góc β
Hướng dẫn giải
Bài 3: Hãy nêu cách dựng góc nhọn β theo hình 18 và chứng minh cách dựng đó là đúng.
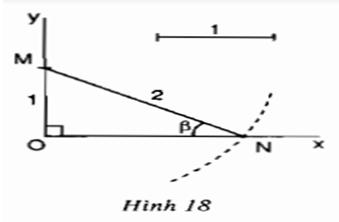
Hướng dẫn giải
- Dựng đoạn OM trên trục Oy sao cho OM = 1
- Dựng đường tròn tâm M bán kính bằng 2, đường tròn giao với tia Ox tại N
- Khi đó góc MNO là góc cần dựng
Chứng minh:
Tam giác MON vuông tại O có: MO = 1; MN = 2
Khi đó:
sinβ = sin(MNO) = MO/MN = 1/2 = 0,5
Bài 4: Cho hình 19. Hãy cho biết tổng số đo của góc α và góc β. Lập các tỉ số lượng giác của góc α và góc β. Trong cặp tỉ số này, hãy cho biết các cặp tỉ số bằng nhau.
Hướng dẫn giải
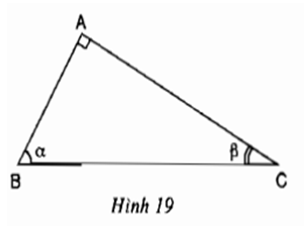
⇒ sin α = cos β
cos α = sin β
tan α = cot α
cot α = tan β
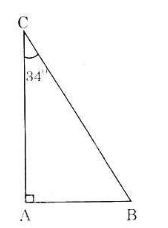
Bài 5: Vẽ một tam giác vuông có một góc nhọn 34o rồi viết các tỉ số lượng giác của góc 34o.
Hướng dẫn giải
ΔABC vuông tại A có góc C = 34o.
Khi đó:
Tỉ số lượng giác của góc là:
Bài 6: Cho tam giác ABC vuông tại C, trong đó AC = 0,9m, BC = 1,2m. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.
Hướng dẫn giải
Xét vuông tại C, áp dụng định lí Pytago, ta có:
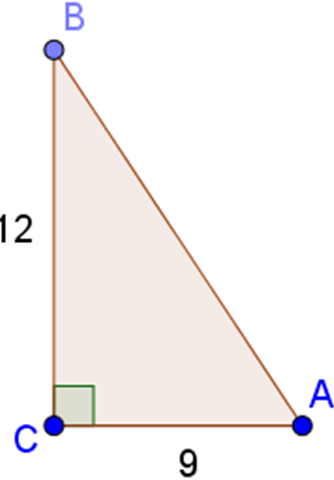
Vì vuông tại C nên góc B và A là hai góc phụ nhau. Do vậy, ta có:
Nhận xét: Với hai góc phụ nhau, ta có sin góc này bằng cosin góc kia, tan góc này bằng cotan góc kia!
Bài 7: Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45o: sin60o, cos75o, sin52o30', cotg82o, tg80o
Hướng dẫn giải
(Áp dụng tính chất lượng giác của hai góc phụ nhau.)
Vì 60o + 30o = 90o nên sin60o = cos30o
Vì 75o + 15o = 90o nên cos75o = sin15o
Vì 52o30' + 37o30' = 90o nên sin 52o30'= cos37o30'
Vì 82o + 8o = 90o nên cotg82o = tg8o
Vì 80o + 10o = 90o nên tg80o = cotg10o




