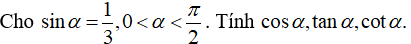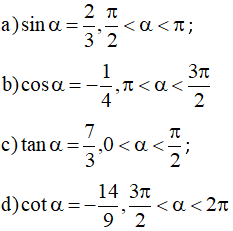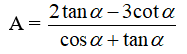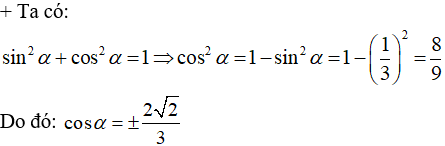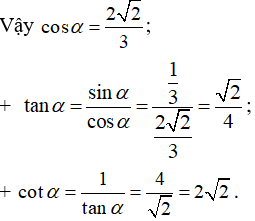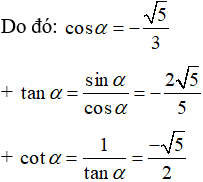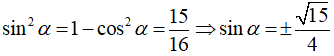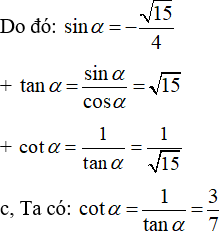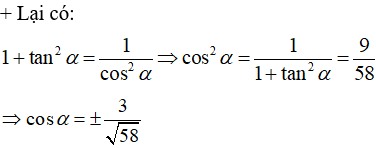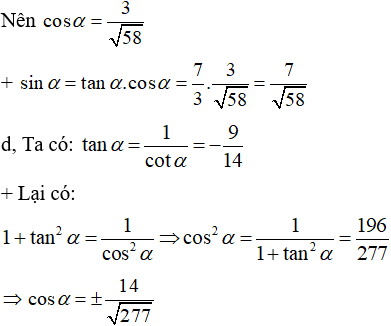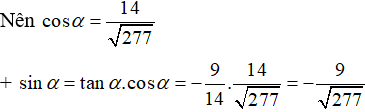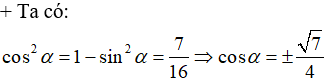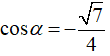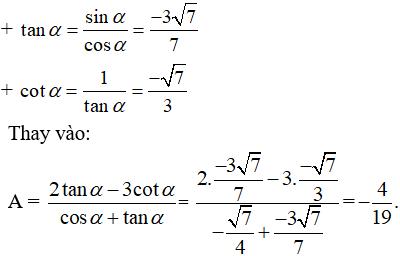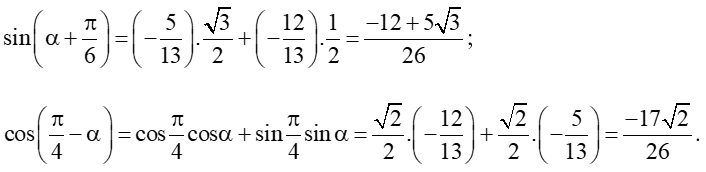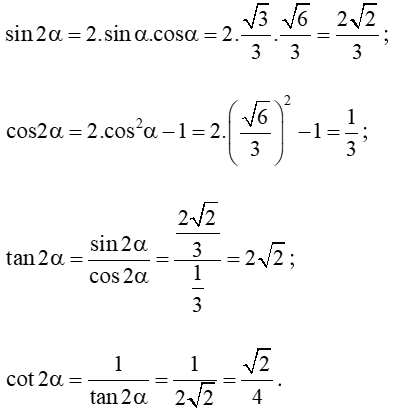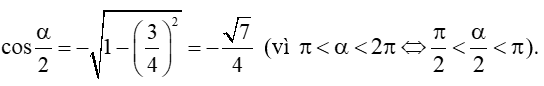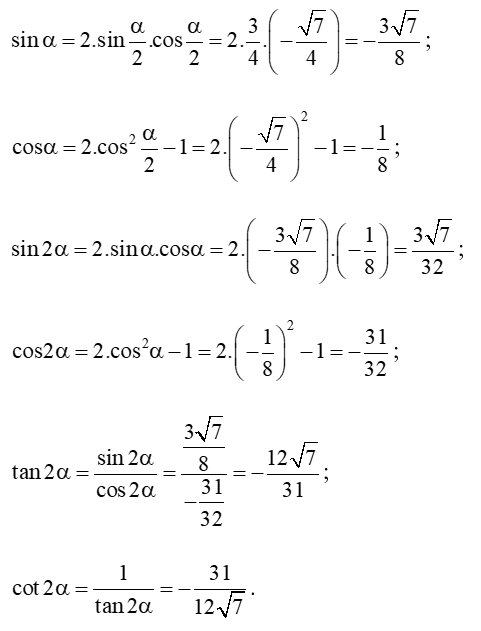Tính giá trị lượng giác của góc anpha
Lí thuyết
1. Định nghĩa giá trị lượng giác của một góc bất kì từ 0o đến 180o
Với mỗi góc α (0o ≤ α ≤ 1800) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho góc ∠xOM = α và giả sử điểm M có tọa độ M(x0;y0)
Khi đó ta có định nghĩa:
+ sin của góc α là y0, kí hiệu là sinα = y0
+ cosin của góc α là x0, kí hiệu là cosα = x0
+ tang của góc α là y0x0 (x0≠ 0), ký hiệu tanα = y0x0
+ cotang cuả góc α là x0y0(y0≠0), ký hiệu cotα = x0y0
Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α
2. Tính chất giá trị lượng giác của một góc bất kì từ 0o đến 180o
Trên hình bên ta có dây cung NM song song với trục Ox và nếu ∠xOM = α thì ∠xON = 180o – α. Ta có yM = yN = yo, xM = –xN = xo. Do đó
+ sin α = sin(180o – α)
+ cos α = –cos(180o – α)
+ tan α = –tan(180o – α)
+ cot α = –cot(180o – α)
3. Công thức Lượng giác cơ bản
Thơ nhớ hàm lượng giác cơ bản
Sin bình cộng cos bình thì phải bằng 1
Sin bình thì bằng tan bình trên tan bình cộng 1
Cos bình bằng một trên một cộng tan bình
Một trên sin bình bằng 1 cộng cot bình
Một trên cos bình bằng một cộng tan bình
Bắt được quả tan,
Sin nằm trên cos,
Cot cải lại,
Cos nằm trên sin.
Hoặc là:
Bắt được quả tan,
Sin nằm trên cos (tan x = sin x / cos x),
Cot dại dột,
Bị cos đè cho (cot x = cos x / sin x).
4. Công thức cộng lượng giác
Thơ công thức cộng
Cos cộng cos thì bằng hai cos cos
Cos trừ cos phải bằng trừ hai sin sin
Sin cộng sin thì bằng hai sin cos
Sin trừ sin bằng hai cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin nhớ nha dấu trừ
Tan tổng thì lấy tổng tan
Chia một trừ với tích tan, dễ mà.
5. Công thức nhân
Công thức nhân đôi:
Công thức nhân ba:
Công thức nhân bốn:
6. Công thức hạ bậc
Thực ra những công thức này đều được biến đổi ra từ công thức lượng giác cơ bản, ví dụ như:
sin2a=1 - cos2a = 1 - (cos2a + 1)/2 = (1 - cos2a)/2.
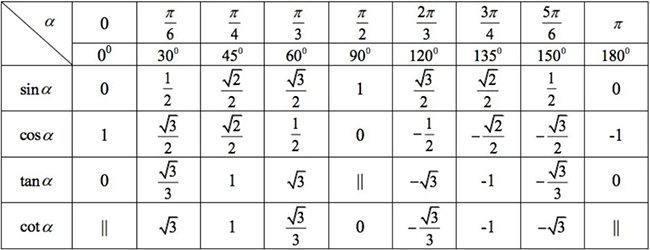
7. Bảng giá trị lượng giác một số góc đặc biệt
Các dạng bài tập lượng giác cơ bản
1. Dạng 1: Tìm các giá trị lượng giác của một cung khi biết một giá trị lượng giác.
Phương pháp:
+ Nếu biết trước sinα thì dùng công thức: sin2α + cos2α = 1 để tìm , lưu ý: xác định dấu của các giá trị lượng giác để nhận, loại.
hoặc cotα = 1/tanα
+ Nếu biết trước cosα thì tương tự như trên.
+ Nếu biết trước tanα thì dùng công thức: 1 + tan2α = 1/cos2α để tìm cosα, lưu ý:xác định dấu của các giá trị lượng giác để nhận, loại. sinα = tanα.cosα, cotα = 1/tanα
Lưu ý :
Với các dạng bài tập lượng giác lớp 10 cơ bản, phải nắm rõ các cung phần tư từ đó xác định dấu của các giá trị lượng giác; để xác định dấu của các giá trị lượng giác ta cần nắm rõ định nghĩa giá trị lượng giác của cung α và thực hiện như sau: Vẽ đường tròn lượng giác, trục đứng(Oy) là trục sin, trục nằm (Ox) là trục cosin; khi thuộc cung phần tư nào ta cho một điểm M bất kì nằm trên cung phần tư đó, sau đó chiếu điểm M vuông góc xuống trục sin và trục cos từ đó xác định được sin dương hay âm, cos dương hay âm; tan=sin/cos; cot=cos/sin; dựa vào dấu của sin và cos ta xác định được dấu của tan và cot theo nguyên tắc chia dấu: -/-=+; -/+= -
2. Dạng 2: Chứng minh các biểu thức lượng giác
Phương pháp :
Sử dụng các công thức lượng giác kết hợp với các hằng đẳng thức đại số (7 hằng đẳng thức đáng nhớ) và các hằng đẳng thức lượng giác cơ bản để biến đổi một vế thành vế kia.
3. Dạng 3: Rút gọn biểu thức lượng giác
Phương pháp:
Tương tự như dạng toán chứng minh biểu thức lượng giác. Trong các dạng bài tập lượng giác lớp 10 cơ bản đây là hai dạng toán tương tự cách giải. Tuy nhiên, dạng toán rút gọn ta chưa biết được vế phải nên cần phải biến đổi một cách cẩn thận để ra biểu thức đúng.
4. Dạng 4: Tính giá trị của một biểu thức lượng giác:
Phương pháp:
Để tính giá trị các biểu thức này ta phải biến đổi chúng về một biểu thức theo sin(tan) rồi thay giá trị của sin(tan) vào biểu thức đã biến đổi.
5. Dạng 5: Chứng minh một biểu thức lượng giác không phụ thuộc vào x
Phương pháp:
Dùng các công thức lượng giác để biến đổi biểu thức đã cho ra kết quả không chứa x.
Ví dụ:
6. Dạng 6: Tính giá trị của một biểu thức lượng giác.
Phương pháp:
Dùng các hệ thức cơ bản và giá trị lượng giác của các góc có liên quan đặc biệt
Giá trị lượng giác các góc có liên quan đặc biệt : bù nhau, phụ nhau, đối nhau, hơn kém pi.
+ Chú ý: Với k € Z ta có:
sin(α + k2π) = sinα
cos(α + k2π) = cosα
tan(α + kπ) = tanα
cot(α = kπ) = cotα
Ví dụ:
7. Dạng 7: Các bài toán trong tam giác:
Phương pháp:
Trong một tam giác tổng 3 góc bằng 180o
A + B + C = π
Trong các dạng bài tập lượng giác lớp 10 cơ bản thì đây là một dạng bài tập khó yêu cầu các em phải liên hệ giữa lượng giác và hình học. Do đó, phải nắm được mối quan hệ giữa các góc đặc biệt trong tam giác.
Ví dụ: Chứng minh rằng trong tam giác ABC ta có:
Bài tập vận dụng (có đáp án)
Bài 1:
Bài 2: Tính các giá trị lượng giác của góc α, nếu:
Bài 3: Biết 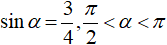
Bài 4: Tính các giá trị lượng giác của góc α, nếu
a) cosα = −¼, π<α<3π/2
b) sinα = ⅔, π/2<α<π
c) tanα= 7/3, 0<α<π/2
d) cotα =− 14/9, 3π/2<α<2π
Bài 5. Tính các giá trị lượng giác của góc α, nếu
a) cosα = 4/13 và 0 < α < π/2
b) sinα = -0,7và π < α < 3π/2
c) tanα = (-5)/17 và π/2 < α < π
d) cotα = -3 và 3π/2 < α < 2π
Bài 6: Chứng minh đẳng thức sau:
sin(a + b) sin(a – b) = sin2 a – sin2 b = cos2 b – cos2 a.
Bài 7: Cho tam giác ABC có ; và a = BC = 12 cm.
a) Sử dụng công thức và định lí sin, hãy chứng minh diện tích của tam giác ABC cho bởi công thức
.
b) Sử dụng kết quả ở câu a và công thức biến đổi tích thành tổng, hãy tính diện tích S của tam giác ABC.
Bài 8: Tính biết sin và .
Bài 9: Tính các giá trị lượng giác của góc 2α, biết:
a) sin = và ;
b) sin và .
Bài 10: Chứng minh rằng tam giác ABC, ta có sinA = sinB.cosC + sinC.cosB.
Hướng dẫn giải:
Bài 1:
Vì 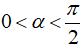
Bài 2:
Vì 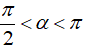
b, Ta có:
Vì 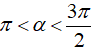
Vì 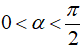
Vì 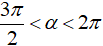
Bài 3:
Vì 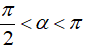
Bài 4:
Bài 5:
a) Vì 0 < α < π/2 nên sin α > 0; tan α > 0; cot α > 0
* Từ cos2α + sin2α = 1, ta có:
(4/13)2 + sin2 α = 1 ⇔ sin2 α = 1 – 16/169
⇔ sin α = (3√17)/13
* Từ tan α = sinα/cosα, ta có tan α = (3√17)/4
* Từ cot α = cosα/sinα, ta có cot α = 4/(3√17)
b) Vì π < α < 3π/2 nên cosα < 0;tanα > 0;cotα>0
* Từ cos2 α + sin2 α = 1, ta có:
cos2 α = 1 – (0,7)2 = 0,51 = 51/100 => cos α = (-√51)/10
* Từ tan α=(cos α)/(sin α) ta có tan α=(-0,7.10)/(-√51)
=> tan α = (7√51)/51
* Từ cot α = 1/(tan α), ta có tan α=√51/7
c) Vì π/2 < α < π, nên cos α < 0; sin α > 0; cot α < 0
* Từ cot α.tan α = 1, ta có cot α = (-7)/15
* Từ cos2α = 1/(1 + tan2 α) ta có cos2α=1/(1+(-15/7)2 )
=> cos α = (-7)/√274
* Từ sin2α=1/(1+cos2 α), ta có sin α=15/√274
d) Vì 3π/2 < α < 2π nên sin α < 0; cos α > 0; tan α < 0
Tương tự ta có kết quả sin α = (-1)/√10;cosα = 3/√(10 );tanα = -1/3
Bài 6:
Ta có: sin(a + b) sin(a – b) = [cos(a + b – a + b) – cos(a + b + a – b)]
= [cos 2b – cos 2a] = [(2cos2 b – 1) – (2cos2 a – 1)] = cos2 b – cos2 a.
Vậy sin(a + b) sin(a – b) = cos2 b – cos2 a (1).
Lại có, cos 2b – cos 2a = (1 – 2sin2 b) – (1 – 2sin2 a) = 2(sin2 a – sin2 b)
Do đó, [cos 2b – cos 2a] = . 2(sin2 a – sin2 b) = sin2 a – sin2 b.
Vậy sin(a + b) sin(a – b) = sin2 a – sin2 b (2).
Từ (1) và (2), suy ra sin(a + b) sin(a – b) = sin2 a – sin2 b = cos2 b – cos2 a (đpcm).
Bài 7:
a) Định lí sin trong tam giác ABC với BC = a, AC = b và AB = c là:
Từ đó suy ra .
Diện tích tam giác ABC là .
Vậy (đpcm).
b) Ta có: (định lí tổng ba góc trong tam giác ABC).
.
Ta có:
.
Vậy diện tích của tam giác ABC là (cm2).
Bài 8:
Ta có: cos (vì ).
Ta lại có:
Bài 9:
a) Ta có: 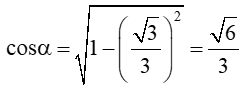
Khi đó:
b) Ta có:
Khi đó:
Bài 10:
Xét tam giác ABC, có:
A + B + C = 180° ⇒ A = 180° – (B + C)
sinA = sin(180° – (B + C)) = sin(B + C) = sinB.cosC + sinC.cosB.
Bài tập tự luyện
Bài 1. Cho góc lượng giác α sao cho và . Tìm cosα.
Bài 2: Cho α + β = π. Tính:
a) A = sin2α + cos2β;
b) B = (sinα + cosβ)2 + (cosα + sinβ)2.
Bài 3: Tính các giá trị lượng giác của góc α trong mỗi trường hợp sau:
a) với ;
b) với ;
c) tanα = 3 với ‒π < α < 0;
d) cotα = ‒2 với 0 < α < π.
Bài 4: Tính:
a) ;
b) tan1° . tan2° . tan45° . tan88° . tan89°.
Bài 5: Cho góc lượng giác α. So sánh:
a) cos2α + sin2α và 1;
b) tanα . cotα và 1 (với cosα ≠ 0, sinα ≠ 0);
c) và với cosα ≠ 0;
d) và với sinα ≠ 0.
Bài 6: Tính sin 2a, cos 2a, tan 2a, biết:
a) và ;
b) sin a + cos a = và .
Bài 7: Tính giá trị của các biểu thức sau:
a) ;
b) .
Bài 8: Chứng minh rằng:
a) sin x – cos x = ;
b) .
Bài 9: Không dùng máy tính, tính giá trị của biểu thức
Bài 10: Tính:
a) , biết và ;
b) , biết và .
Xem thêm các dạng bài tập Toán lớp 11 đầy đủ, chi tiết và hay khác:
90 Bài tập giá trị lượng giác của một góc từ 0 độ đến 180 độ (có đáp án năm 2023) - Toán 10
150 Bài tập về hàm số lượng giác (có đáp án năm 2023) - Toán 11
500 Bài tập Toán 11 chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án năm 2023)
70 Bài tập về đạo hàm của hàm số lượng giác (có đáp án năm 2023) - Toán 11
70 Bài tập về giới hạn của dãy số (có đáp án năm 2023) - Toán 11