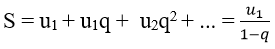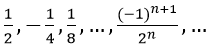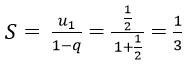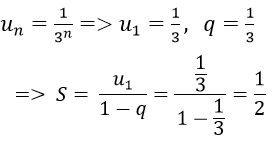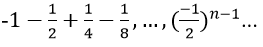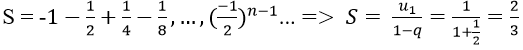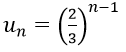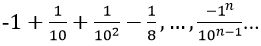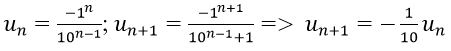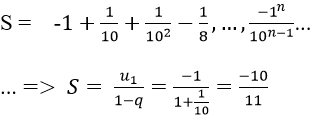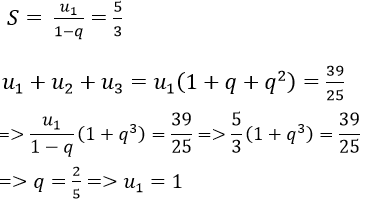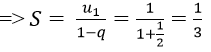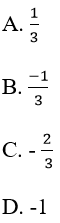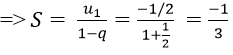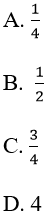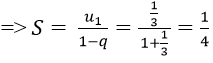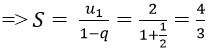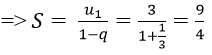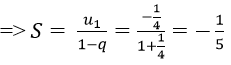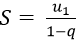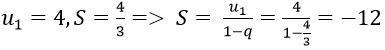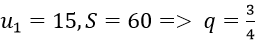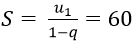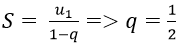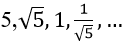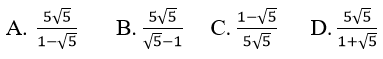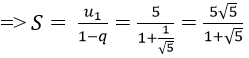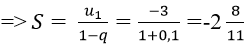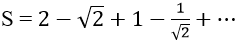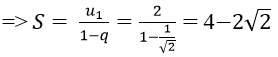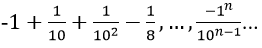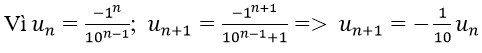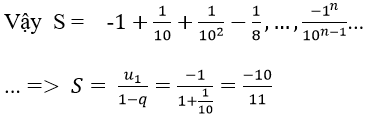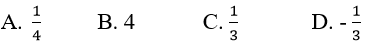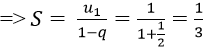30 Bài tập Cách tính tổng của cấp số nhân lùi vô hạn (2024)cực hay có đáp án

Cách tính tổng của cấp số nhân lùi vô hạn

1. Phương pháp giải

Tổng của CSN lùi vô hạn

Cấp số nhân vô hạn u₁, u₂, u₃,..u_n,..có công bội q, với |q| < 1 gọi là cấp số nhân lùi vô hạn.

Tổng S của cấp số nhân đó là:

Chú ý: Nếu công bội là:

• Số dương: Các số hạng luôn có dấu cố định.
• Số âm: các số hạng là đan dấu giữa âm và dương..
• 0, mọi số hạng bằng 0.
• Lớn hơn 1, các số hạng tăng theo hàm mũ tới vô cực dương hoặc âm.
  1, là một dãy không đổi.
• Giữa 1 và −1 nhưng khác không, chúng giảm theo hàm mũ về 0.
  −1, là một dãy đan dấu.
• Nhỏ hơn −1, chúng tăng theo hàm mũ về vô cực (dương và âm).

2. Mở rộng về cấp số nhân

2.1. Định nghĩa

Dãy số  được xác định bởi:  thì dãy số này được gọi là cấp số nhân, q là công bội.

Như vậy ta có thể hiểu cấp số nhân có dạng:  với a là số hạng đầu tiên và q là công bội.

Ví dụ: Cấp số nhân có số hạng đầu bằng 2 và công sai bằng 2 là 

2.2. Số hạng tổng quát

Cấp số nhân bắt đầu là phần tử  và công bội q thì số hạng thứ n của cấp số cộng được tính theo công thức: 

2.3. Tổng của một cấp số nhân

Tổng số hạng đầu của cấp số nhân :

Nhân cả 2 vế với: 

Vì tất cả các số hạng khác đã loại trừ lẫn nhau

3. Ví dụ minh họa

Ví dụ 1: Tìm tổng của cấp số nhân vô hạn sau:

Hướng dẫn:

Đây là tổng của cấp số nhân vô hạn có

 nên tổng là 

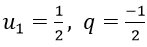
Ví dụ 2: Tìm tổng của cấp số nhân lùi vô hạn (u_n) biết u_n = 1/(3ⁿ)

Hướng dẫn:

Vì

Ví dụ 3: Tìm tổng của cấp số nhân vô hạn:

Hướng dẫn:

Vì các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = 1, q = -1/2

Vậy

Ví dụ 4: Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội q = 2/3

Hướng dẫn:

Ví dụ 5: Tìm tổng của dãy số sau:

Hướng dẫn:

Vì vậy các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = -1, q = -1/10

Vậy

Ví dụ 6: Tổng của một cấp số nhân lùi vô hạn là 5/3 tổng ba số hạng đầu tiên của nó là 39/25. Tìm số hạng đầu và công bội của cấp số đó.

Hướng dẫn:

Ta có

Ví dụ 7: Cho dãy số (u_n) với 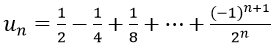. Tính tổng của dãy u_n

Hướng dẫn:

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

4. Bài tập vận dụng (có đáp án)

Bài 1: Tổng của cấp số nhân vô hạn: 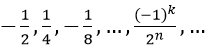 là:

Lời giải:

Đáp án: B

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = (-1)/2 và q = (-1)/2.

Chọn đáp án B

Bài 2: Tổng của cấp số nhân vô hạn: 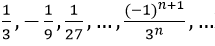 là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/3 và q = (-1)/3.

Chọn đáp án A

Bài 3: Tổng của cấp số nhân vô hạn 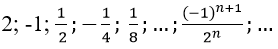 là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 2 và q = (-1)/2.

Chọn đáp án A

Bài 4: Tổng của cấp số nhân vô hạn 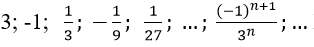 là:

Lời giải:

Đáp án: C

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 3 và q = (-1)/3.

Chọn đáp án C

Bài 5: Tổng của cấp số nhân vô hạn: 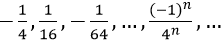 là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = (-1)/4 và q = (-1)/4.

Chọn đáp án A

Bài 6: Kết quả nào sau đây là đúng:

A. Cấp số nhân lùi vô hạn (u_n) có công bội q thì tổng 

B. Cấp số nhân lùi vô hạn (u_n) có

C. Cấp số nhân lùi vô hạn (u_n) có 

D. Cấp số nhân lùi vô hạn (u_n) có 

Lời giải:

Đáp án: C

Vì q = (3/4) < 1 đây là cấp số nhân lùi vô hạn nên 

Chọn C

Bài 7: Cấp số nhân lùi vô hạn (u_n) có u₁ = -50, S = 100. Tìm 5 số hạng đầu tiên của dãy:

A. 50; 25; 12,5; 6,5; 3,25

B. 50; 25,5; 12,5; 6,25; 3,125

C. 50; 25; 12,5; 6,25; 3,125

D. 50; 25; 12,25; 6,125; 3,0625

Lời giải:

Đáp án: C

Áp dụng công thức : 

Suy ra 5 số hạng đầu tiên của dãy số: 50; 25; 12,5; 6,25; 3,125

Chọn C

Bài 8: Cấp số nhân lùi vô hạn (u_n) có u₁ = -1, q = x. Tìm tổng S và 3 số hạng đầu của cấp số này:

A.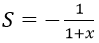 và -1, x, -x²

B.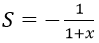 và -1, x, x²

C.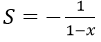 và -1, -x, -x²

D.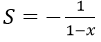 và -1, x, -x²

Lời giải:

Đáp án: C

 số hạng đầu là -1, -x, -x²

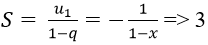
Chọn C

Bài 9: Cấp số nhân lùi vô hạn (u_n) có u₁ = -x, q = x². Tìm tổng S và 3 số hạng đầu của cấp số này:

A.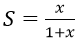 và -x, x³, x⁵

B.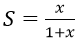 và -x, x³, x⁴

C.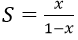 và -x, x³, x⁶

D.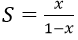 và -x, -x³, -x⁶

Lời giải:

Đáp án: D

 số hạng đầu là - x, -x³, -x⁶

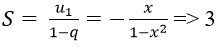
Chọn D

Bài 10: Tìm tổng của cấp số nhân vô hạn sau: 

Lời giải:

Đáp án: D

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 5 và q = 1/√5.

Chọn đáp án D

Bài 11: Tìm tổng của cấp số nhân vô hạn sau: -3; 0,3; -0,03; 0,003;...

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = -3 và q = 0,1

Chọn đáp án A

Bài 12: Tìm tổng 

A. 4 + 2√2

B. 4 - 2√2

C. -4 + 2√2

D. -4 + 2√2

Lời giải:

Đáp án: B

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 2 và q = 1/√2

Chọn đáp án B

Bài 13: Cho cấp số nhân lùi vô hạn sau: 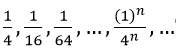 Tìm q

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân nên q = (1/4)

Chọn đáp án A

Bài 14: Tìm tổng của dãy số sau: 

Lời giải:

Đáp án: D

Vì vậy các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = -1, q = (-1)/10

Chọn đáp án D

Bài 15: Cho dãy số (u_n) với 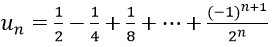. Tính tổng của dãy u_n

Lời giải:

Đáp án: C

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

Chọn đáp án C

Xem thêm các dạng bài tập liên quan khác:

Các công thức về Cấp số cộng, Cấp số nhân (2024) đầy đủ nhất

30 Bài tập về Cấp số nhân (2024) chi tiết nhất, có đáp án

20 Bài tập Cấp số nhân nâng cao (2024) có lời giải chi tiết nhất

30 Bài tập về Tính tổng của cấp số nhân lùi vô hạn (2024) cực hay

300 Bài tập Toán 11 chương 3: Dãy số - Cấp số cộng và cấp số nhân (có đáp án năm 2024)