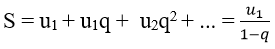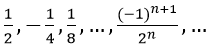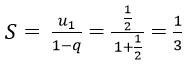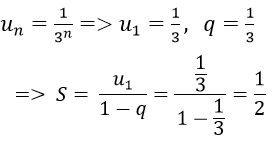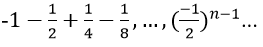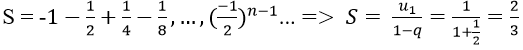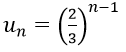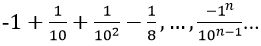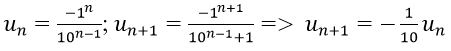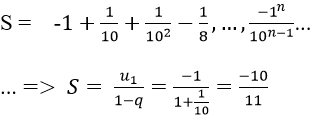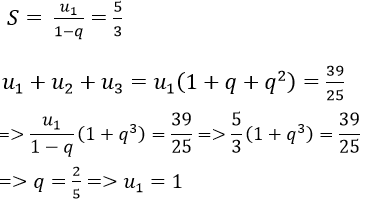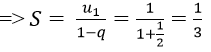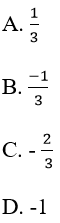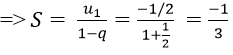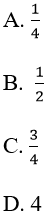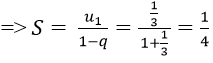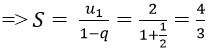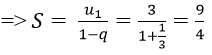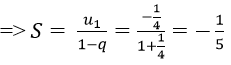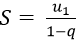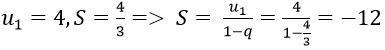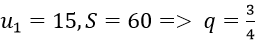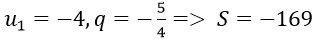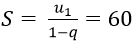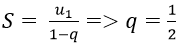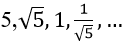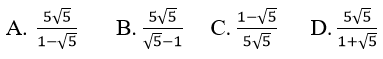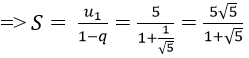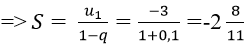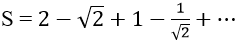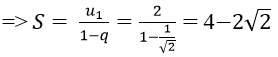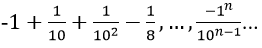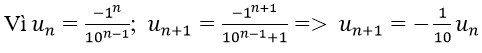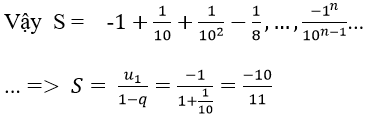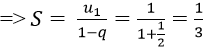30 Bài tập về Tính tổng của cấp số nhân lùi vô hạn (2024) cực hay

Cách tính tổng của cấp số nhân lùi vô hạn cực hay

I. Phương pháp giải

Tổng của CSN lùi vô hạn

Cấp số nhân vô hạn u₁, u₂, u₃,..u_n,..có công bội q, với |q| < 1 gọi là cấp số nhân lùi vô hạn.

Tổng S của cấp số nhân đó là:

Ví dụ minh họa

Ví dụ minh họa 1: Tìm tổng của cấp số nhân vô hạn sau:

Hướng dẫn:

Đây là tổng của cấp số nhân vô hạn có

 nên tổng là 

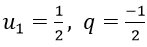
Ví dụ minh họa 2: Tìm tổng của cấp số nhân lùi vô hạn (u_n) biết u_n = 1/(3ⁿ)

Hướng dẫn:

Vì

Ví dụ minh họa 3: Tìm tổng của cấp số nhân vô hạn:

Hướng dẫn:

Vì các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = 1, q = -1/2

Vậy

Ví dụ minh họa 4: Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội q = 2/3

Hướng dẫn:

Ví dụ minh họa 5: Tìm tổng của dãy số sau:

Hướng dẫn:

Vì vậy các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = -1, q = -1/10

Vậy

Ví dụ minh họa 6: Tổng của một cấp số nhân lùi vô hạn là 5/3 tổng ba số hạng đầu tiên của nó là 39/25. Tìm số hạng đầu và công bội của cấp số đó.

Hướng dẫn:

Ta có

Ví dụ minh họa 7: Cho dãy số (u_n) với 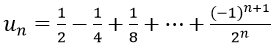. Tính tổng của dãy u_n

Hướng dẫn:

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

II. Bài tập vận dụng (có đáp án)

Bài 1: Tổng của cấp số nhân vô hạn: 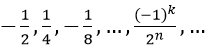 là:

Lời giải:

Đáp án: B

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = (-1)/2 và q = (-1)/2.

Chọn đáp án B

Bài 2: Tổng của cấp số nhân vô hạn: 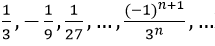 là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/3 và q = (-1)/3.

Chọn đáp án A

Bài 3: Tổng của cấp số nhân vô hạn 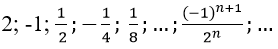 là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 2 và q = (-1)/2.

Chọn đáp án A

Bài 4: Tổng của cấp số nhân vô hạn 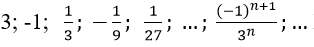 là:

Lời giải:

Đáp án: C

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 3 và q = (-1)/3.

Chọn đáp án C

Bài 5: Tổng của cấp số nhân vô hạn: 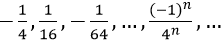 là:

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = (-1)/4 và q = (-1)/4.

Chọn đáp án A

Bài 6: Kết quả nào sau đây là đúng:

A. Cấp số nhân lùi vô hạn (u_n) có công bội q thì tổng 

B. Cấp số nhân lùi vô hạn (u_n) có

C. Cấp số nhân lùi vô hạn (u_n) có 

D. Cấp số nhân lùi vô hạn (u_n) có 

Lời giải:

Đáp án: C

Vì q = (3/4) < 1 đây là cấp số nhân lùi vô hạn nên 

Chọn C

Bài 7: Cấp số nhân lùi vô hạn (u_n) có u₁ = -50, S = 100. Tìm 5 số hạng đầu tiên của dãy:

A. 50; 25; 12,5; 6,5; 3,25

B. 50; 25,5; 12,5; 6,25; 3,125

C. 50; 25; 12,5; 6,25; 3,125

D. 50; 25; 12,25; 6,125; 3,0625

Lời giải:

Đáp án: C

Áp dụng công thức : 

Suy ra 5 số hạng đầu tiên của dãy số: 50; 25; 12,5; 6,25; 3,125

Chọn C

Bài 8: Cấp số nhân lùi vô hạn (u_n) có u₁ = -1, q = x. Tìm tổng S và 3 số hạng đầu của cấp số này:

A.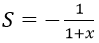 và -1, x, -x²

B.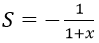 và -1, x, x²

C.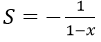 và -1, -x, -x²

D.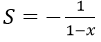 và -1, x, -x²

Lời giải:

Đáp án: C

 số hạng đầu là -1, -x, -x²

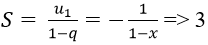
Chọn C

Bài 9: Cấp số nhân lùi vô hạn (u_n) có u₁ = -x, q = x². Tìm tổng S và 3 số hạng đầu của cấp số này:

A.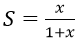 và -x, x³, x⁵

B.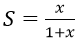 và -x, x³, x⁴

C.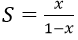 và -x, x³, x⁶

D.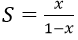 và -x, -x³, -x⁶

Lời giải:

Đáp án: D

 số hạng đầu là - x, -x³, -x⁶

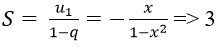
Chọn D

Bài 10: Tìm tổng của cấp số nhân vô hạn sau: 

Lời giải:

Đáp án: D

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 5 và q = 1/√5.

Chọn đáp án D

Bài 11: Tìm tổng của cấp số nhân vô hạn sau: -3; 0,3; -0,03; 0,003;...

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = -3 và q = 0,1

Chọn đáp án A

Bài 12: Tìm tổng 

A. 4 + 2√2

B. 4 - 2√2

C. -4 + 2√2

D. -4 + 2√2

Lời giải:

Đáp án: B

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 2 và q = 1/√2

Chọn đáp án B

Bài 13: Cho cấp số nhân lùi vô hạn sau: 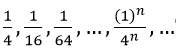 Tìm q

Lời giải:

Đáp án: A

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân nên q = (1/4)

Chọn đáp án A

Bài 14: Tìm tổng của dãy số sau: 

Lời giải:

Đáp án: D

Vì vậy các số của tổng lập thành cấp số nhân lùi vô hạn với u₁ = -1, q = (-1)/10

Chọn đáp án D

Bài 15: Cho dãy số (u_n) với 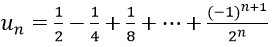. Tính tổng của dãy u_n

Lời giải:

Đáp án: C

Vì u_n là tổng n số hạng đầu tiên của một cấp số nhân có u₁ = 1/2 và q = (-1)/2.

Chọn đáp án C

Xem thêm các dạng bài tập toán hay khác:

300 Bài tập: Dãy số - Cấp số cộng và cấp số nhân (có đáp án năm 2024)

120 Bài tập về cấp số cộng (có đáp án năm 2024)

70 Bài tập về dãy số (có đáp án năm 2024)

60 Bài tập về phương pháp quy nạp toán học (có đáp án năm 2024)

70 Bài tập về phép thử và biến cố (có đáp án năm 2024)