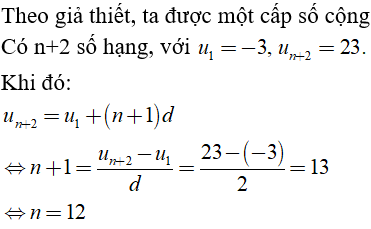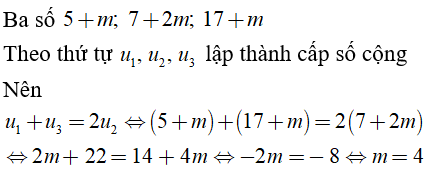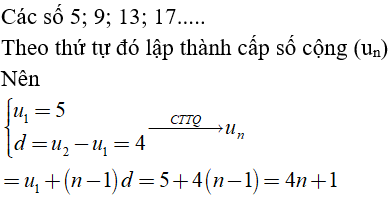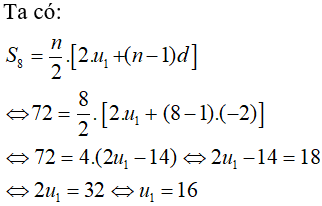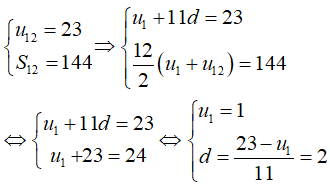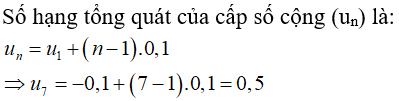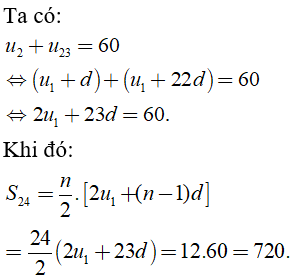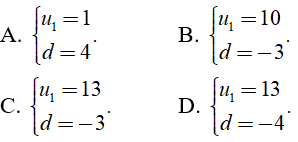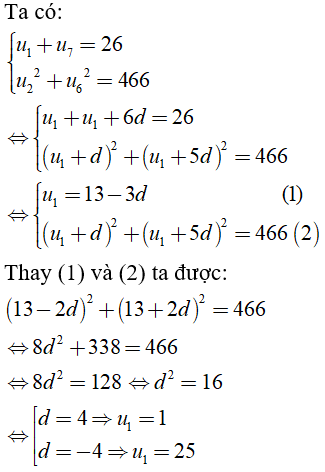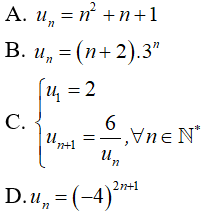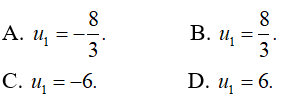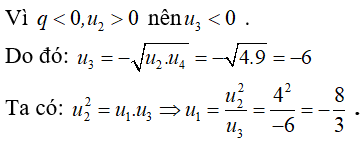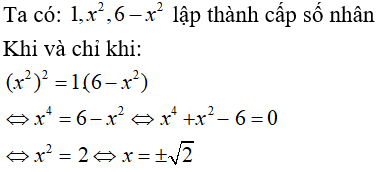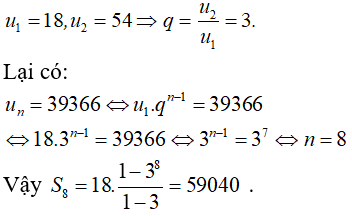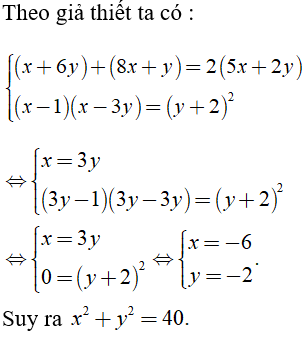CẤP SỐ CỘNG, CẤP SỐ NHÂN
Lý thuyết tổng hợp
1. Cấp số cộng
a. Định nghĩa
Dãy số là một cấp số cộng nếu với mọi , là hằng số.
được gọi là công sai.
* : CSC là một dãy số không đổi.
Ví dụ:
Dãy số là một cấp số cộng vì:
Đây là CSC có công sai và số hạng đầu .
b. Số hạng tổng quát
Kí hiệu: . ( n là số tự nhiên bất kì lớn hơn 1)
Như vậy công sai còn có thể tính bởi công thức: .
Ví dụ:
Cho CSC biết . Tìm .
Ta có:
c. Tính chất
với hay
Ví dụ:
Cho ba số theo thứ đó lập thành một CSC. Tìm
Ta có: .
Vậy .
d. Tổng n số hạng đầu
+) Thông qua số hạng đầu, cuối và số số hạng: , với
+) Thông qua số hạng đầu, số số hạng và công sai:
2. Cấp số nhân
a. Định nghĩa
là cấp số nhân , với
Công bội .
Ví dụ:
Cho cấp số nhân thỏa mãn . Tính .
Ta có: .
b. Số hạng tổng quát
Ví dụ:
Cho cấp số nhân thỏa mãn . Tính .
Ta có:
.
c. Tính chất
hay với
Ví dụ:
Cho bốn số theo thứ tự đó lập thành một CSN. Tìm .
Ta có:
Vậy .
d. Tổng n số hạng đầu
, .
Bài tập vận dụng (có đáp án)
Câu 1: Cho hai số -3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành cấp số cộng có công sai d = 2. Tìm n?
A. n = 12
B.n = 13
C. n = 14
D. n = 15
Chọn đáp án A
Câu 2: Nếu các số 5 + m; 7 + 2m; 17 + m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?
A. m = 2
B.m = 3
C. m = 4
D. m = 5
Chọn đáp án C
Câu 3: Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17;..... Tìm số hạng tổng quát un của cấp số cộng.
A. un = 5n + 1
B. un = 5n - 1
C. un = 4n + 1
D. un = 4n - 1
Chọn đáp án C
Câu 4: Cho cấp số cộng (un) có d = -2 và S8 = 72. Tìm số hạng đầu tiên u1?
A. 16
B. – 16
C. 4
D. 8
Chọn đáp án A
Câu 5: Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng thứ mười hai bằng 23. Khi đó công sai d của cấp số cộng đã cho là bao nhiêu?
A. d = 2
B. d = 3
C. d = 4
D. d = 5
Chọn đáp án A
Câu 6: Cho cấp số cộng (un) có: u1 = -0,1; d = 0,1. Số hạng thứ 7 của cấp số cộng này là:
A. 1, 6
B. 6
C. 0,5
D. 0,6
Chọn đáp án C
Câu 7: Cho cấp số cộng (un) thỏa mãn: 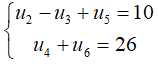
A. d = 2
B. d = 4
C. d = 3
D. d = 5
Chọn đáp án C
Câu 8: Cho cấp số cộng (un) thỏa mãn u2 + u23 = 60. Tính tổng S24 của 24 số hạng đầu tiên của cấp số cộng đã cho.
A. 60
B. 120
C. 720
D. 1440
Chọn đáp án C
Câu 9: Cho cấp số cộng (un) thỏa mãn 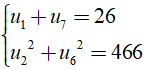
Chọn đáp án A
Câu 10: Trong các dãy số (un) sau, dãy nào là cấp số nhân?
Chọn đáp án D
Câu 11: Cho cấp số nhân (un) với công bội q < 0 và u2 = 4, u4 = 9. Tìm u1 .
Chọn đáp án A
Câu 12: Cho cấp số nhân (un) biết u1 + u5 = 51; u2 + u6 = 102. Hỏi số 12288 là số hạng thứ mấy của cấp số nhân (un) ?
A. Số hạng thứ 10.
B. Số hạng thứ 11.
C. Số hạng thứ 12.
D. Số hạng thứ 13.
Chọn đáp án D
Câu 13: Tìm x biết 1, x2, 6 - x2 lập thành cấp số nhân.
A. x = ± 1
B. x = ± 1
C. x = ± √2
D. x = ± √3
Chọn đáp án B
Câu 14: Tính tổng tất cả các số hạng của một cấp số nhân , biết số hạng đầu bằng 18, số hạng thứ hai bằng 54 và số hạng cuối bằng 39366.
A. 19674.
B. 59040.
C. 177138.
D. 6552
Chọn đáp án B
Câu 15: Các số x + 6y ; 5x + 2y; 8x + y theo thứ tự đó lập thành một cấp số cộng; đồng thời các số x- 1 ; y + 2 ; x – 3y theo thứ tự đó lập thành một cấp số nhân. Tính x2 + y2
A. 40
B. 25
C. 100
D. 10
Chọn đáp án A
Xem thêm các dạng bài tập toán hay khác:
300 Bài tập Toán 11 chương 3: Dãy số - Cấp số cộng và cấp số nhân (có đáp án năm 2023)
120 Bài tập về cấp số nhân (có đáp án năm 2023)
120 Bài tập về cấp số cộng (có đáp án năm 2023)
30 bài tập Cách tính tổng của cấp số nhân lùi vô hạn cực hay có đáp án (2024)
20 Bài tập Cấp số nhân nâng cao (2024) có lời giải chi tiết nhất