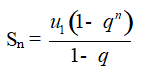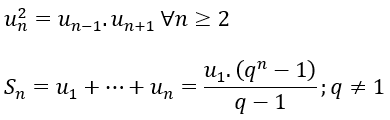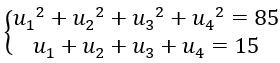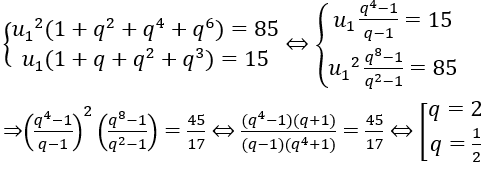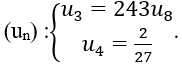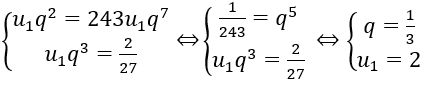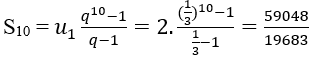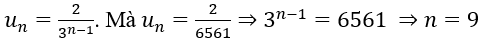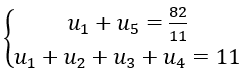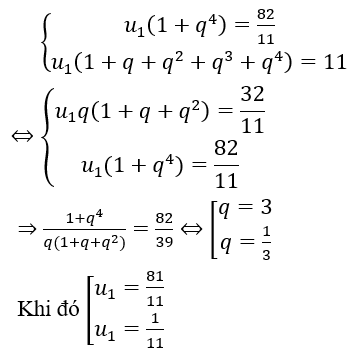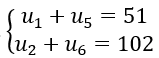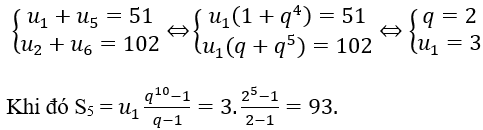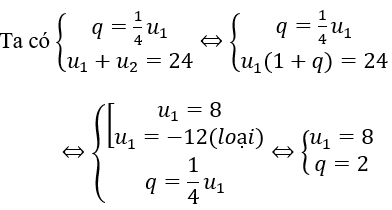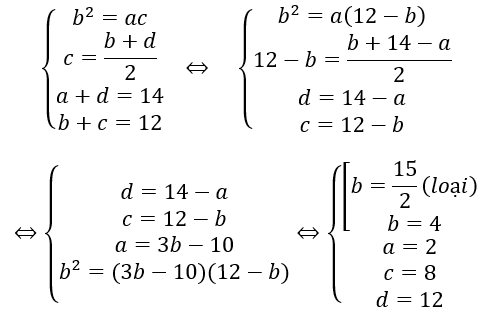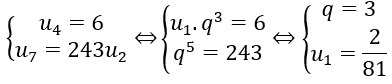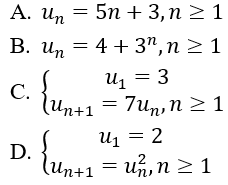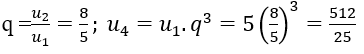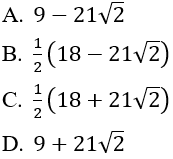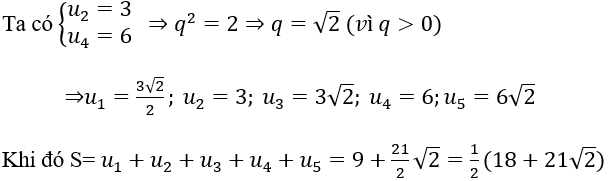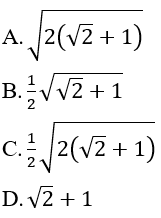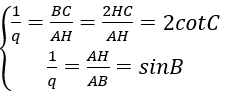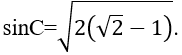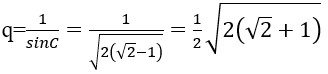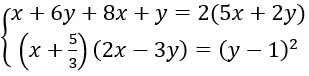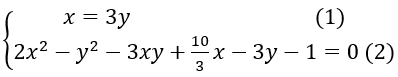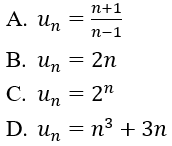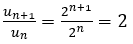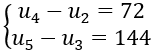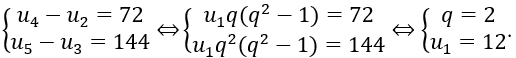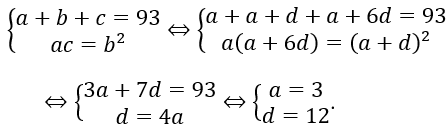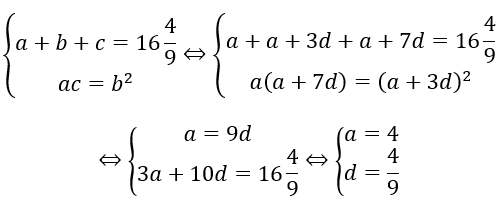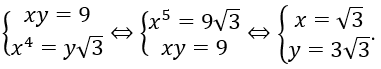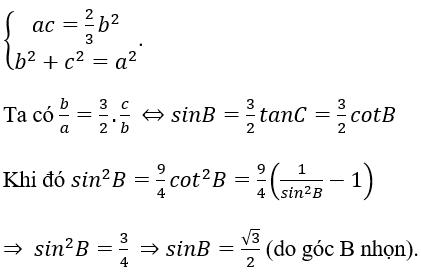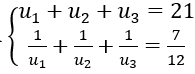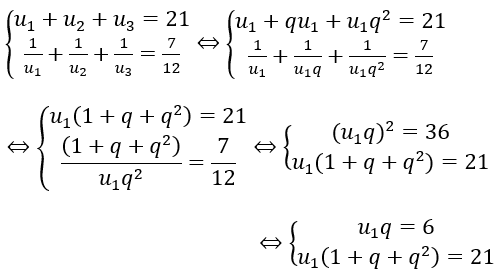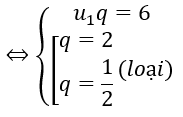30 Bài tập về Cấp số nhân (2024) chi tiết nhất, có đáp án

Cấp số nhân 

LÝ THUYẾT VỀ CẤP SỐ NHÂN

1. Định nghĩa

Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.

Số q được gọi là công bội của cấp số nhân.

Nếu (u_n) là cấp số nhân với công bội q, ta có công thức truy hồi:

    u_n+1 = u_nq với n ∈ N^*

Đặc biệt:

    + Khi q = 0, cấp số nhân có dạng u₁, 0, 0,…, 0,…

    + Khi q = 1, cấp số nhân có dạng u₁, u₁, u₁,…, u₁,…

    + Khi u₁ = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0,…, 0…

2. Số hạng tổng quát

Định lí 1

Nếu cấp số nhân có số hạng đầu u₁ và công bội q thì số hạng tổng quát u_n được xác định bởi công thức

    u_n = u₁.q^n-1 với n ≥ 2

3. Tính chất các số hạng của cấp số nhân

Định lí 2

Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là

    u_k² = u_k-1.u_k+1 với k ≥ 2

4. Tổng n số hạng đầu tiên của một cấp số nhân

Định lí 3

Cho cấp số nhân (u_n) với công bội q ≠ 1. Đặt S_n = u₁ + u₂ + … + u_n. Khi đó

Chú ý: Nếu q = 1 thì cấp số nhân là u₁, u₁, u₁,…, u₁,… khi đó S_n = nu₁.

PHƯƠNG PHÁP GIẢI

Để xác định một cấp số nhân, ta cần xác định số hạng đầu và công bội. Do đó, ta thường biểu diễn giả thiết của bài toán qua u₁ và q.

Số hạng tổng quát của cấp số nhân:

                u_n = u₁.q^n-1, n ≥ 1 .

        Trong đó q: công bội của cấp số nhân.

Tính chất:

VÍ DỤ MINH HỌA

Ví dụ minh họa 1: Cho cấp số nhân (u_n) có các số hạng khác không, tìm u₁ biết:

Đáp án và hướng dẫn giải

Ta có:

Từ đó ta tìm được u₁=1,u₁=8.

Ví dụ minh họa 2: Cho cấp số nhân 

1. Viết năm số hạng đầu của cấp số;

2. Tính tổng 10 số hạng đầu của cấp số;

3. Số 2/6561 là số hạng thứ bao nhiêu của cấp số ?

Đáp án và hướng dẫn giải

Gọi q là công bội của cấp số. Theo giả thiết ta có:

1. Năm số hạng đầu của cấp số là:

u₁=2,u₂=2/3,u₃=2/9,u₄=2/27,u₅=2/81.

2. Tổng 10 số hạng đầu của cấp số

3. Ta có:

Vậy 2/6561 là số hạng thứ 9 của cấp số.

BÀI TẬP VẬN DỤNG (CÓ ĐÁP ÁN)

Bài 1: Cho cấp số nhân (un) có các số hạng khác không, tìm u₁ biết: 

Lời giải:

Bài 2: Tìm tổng 5 số hạng đầu tiên của cấp số nhân, biết 

Lời giải:

Bài 3: Một cấp số nhân dương có 4 số hạng, công bội q bằng 1/4 lần số hạng thứ nhất, tổng của hai số hạng đầu bằng 24. Tìm tích các số hạng cấp số nhân đó?

Lời giải:

Gọi 4 số lập thành cấp số cộng là u₁,u₂,u₃,u₄

u₁=8,u₂=16,u₃=32,u₄=64. Khi đó tích cần tìm là: 8.6.32.64 = 98304.

Bài 4: Cho bốn số nguyên biết rằng ba số hạng đầu lập thành một cấp số nhân, ba số hạng sau lập thành một cấp số cộng. Tổng của hai số hạng đầu và cuối bằng 14, còn tổng hai số ở giữa bằng 12. Tổng của bốn số nguyên đó là?

Lời giải:

Gọi 4 số cần tìm là a,b,c,d. Dựa vào giả thiết ta có hệ:

Vậy tổng 4 số nguyên đó là: 2 + 4 + 8 +12 = 26.

Bài 5: Cho cấp số nhân có 7 số hạng, số hạng thứ tư bằng 6 và số hạng thứ 7 gấp 243 lần số hạng thứ hai. Hãy tìm số hạng còn lại của CSN đó.

Lời giải:

Từ giả thiết ta có

Vậy u₁=2/9,u₂=2/3,u₃=2,u₄=6,u₅=18,u₆=54,u₇=162.

Bài 6: Trong các dãy số sau, dãy số nào là cấp số nhân?

Lời giải:

Đáp án: C

Đáp án là C (CSN với công bội là 7).

Bài 7: Cho cấp số nhân (u_n) có u₁=5; u₂ = 8. Tìm u₄

A. 512/25

B. 125/512

C. 625/512

D. 512/125

Lời giải:

Đáp án: A

Đáp án A

Bài 8: Cho một cấp số nhân có 5 số hạng với công bội dương. Biết rằng số hạng thứ hai bằng 3, số hạng thứ tư bằng 6. Tính tổng của cấp số nhân đó?

Lời giải:

Đáp án: C

Kí hiệu u₁,u₂,u₃,u₄,u₅ là các số hạng của cấp số nhân

Đáp án C

Bài 9: Cho tam giác ABC cân (AB=AC), có cạnh đáy BC, đường cao AH, cạnh bên AB theo thứ tự số đo lập thành một cấp số nhân. Hãy tính công bội q của cấp số nhân đó.

Lời giải:

Đáp án: C

Theo giả thiết AB=AC, BC,AH,AB lập thành cấp số nhân nên ta có hệ:

Từ đó ta có kết quả sau: 2cotC = sinC ⇔ 2cosC =sin²C = 1-cos²C ⇔ cos²C + 2cosC -1 =0 ⇒cosC = -1 +√2 (0º< C < 90º)

Do C là góc nhọn nên 

Cho nên công bội của cấp số nhân là:

Đáp án C.

Bài 10: Tìm các số (x,y) biết y < 0 và các số x+6y, 5x+2y, 8x+y theo thứ tự lập thành cấp số cộng đồng thời các số x+ 5/3, y -1, 2x – 3y theo thứ tự đó lập thành một cấp số nhân.

A. (3, -1)

B. (-3, -1)

C. (-1,-3)

D. (-1,3)

Lời giải:

Đáp án: B

Ta có hệ phương trình:

Từ đó ta suy ra

Thế (1) vào (2) ta được: 8y²+7y-1=0⇒y=-1 hoặc y=1/8

Do y < 0 , ta được y = -1, x = -3

Đáp án B

Bài 11: Trong các dãy số sau dãy số nào là cấp số nhân?

A. 1,3,5,7,9

B. -1,-3,1,3,5

C. 1,2,4,16,256

D. 1,2,4,8,16

Lời giải:

Đáp án: D

Đáp án D (CSN với công bội là 2).

Bài 12: Trong các dãy số sau, dãy nào là dãy số nhân?

Lời giải:

Đáp án: C

Đáp án C vì 

Bài 13: Số hạng đầu tiên của cấp số nhân (u_n) thoả mãn hệ 

A. 2        B. 12        C. 24        D. 0

Lời giải:

Đáp án: B

Đáp án B.

Bài 14: Cho ba số tạo thành một cấp số nhân mà tổng của chúng bằng 93. Ta có thể sắp xếp chúng (theo thứ tự của cấp số nhân kế trên) như là số hạng thứ nhất, thứ hai và thứ bảy của một cấp số cộng. Tìm tích của 3 số đó.

A. 3375

B. 64

C. 2744

D. 1000

Lời giải:

Đáp án: A

Gọi 3 số cần tìm là a, b, c. Vì 3 số trên là số hạng thứ nhất, thứ hai và thứ bảy của một cấp số cộng nên ta có 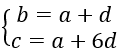 (với d là công sai của cấp số cộng đó).

3 số trên tạo thành cấp số nhân với tổng là 93 nên ta có:

Vậy a = 3, b = 15, c = 75. Tích ba số trên là 3.15.75 = 3375.

Đáp án A.

Bài 15: Tìm số hạng đầu của cấp số nhân có bốn số hạng, biết tổng ba số hạng đầu bằng 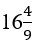, đồng thời theo thứ tự, chúng là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng.

A. 4

B. 16/9

C. 2/3

D. -1

Lời giải:

Đáp án: A

Gọi 4 số cần tìm là a, b, c, d. Vì 3 số hạng đầu là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng nên ta có 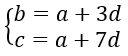 (với d là công sai của cấp số cộng đó).

Từ giả thiết ta có:

Vậy số hạng đầu là 4. Đáp án A.

Bài 16: Cho 3 số x, 3, y lập thành một cấp số nhân và x⁴=y√3. Tìm công bội q của cấp số đó

A. 1/3

B. √3

C. 3

D. 1/√3

Lời giải:

Đáp án: B

Vậy công bội q = √3.

Đáp án B.

Bài 17: Cho tam giác ABC có các cạnh tương ứng a,b,c. Biết 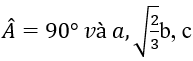 theo thứ tự lập thành một cấp số nhân. Tìm số đo góc B.

A. 30º

B. 45º

C. 15º

D. 60º

Lời giải:

Đáp án: D

Vì 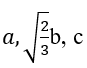 theo thứ tự lập thành một cấp số nhân và tam giác ABC vuông nên ta có:

Đáp án D.

Bài 18: Giả sử a,b,c ,d lập thành một cấp số nhân. Tính giá trị biểu thức

        (a-c)²+(b-c)²+(b-d)²-(a-d)²

A. 3

B. 2

C. 1

D. 0

Lời giải:

Đáp án: D

(a-c)²+(b-c)²+(b-d)²-(a-d)²=2b²+2c²-2ac-2bc-2bd+2ad

Vì a, b, c, d là một cấp số nhân nên ta có: b²=ac,b²=bd.

Khi đó ta có: (a-c)²+(b-c)²+(b-d)²-(a-d)²=2ad-2bc=0.

Đáp án D.

Bài 19: Công bội nguyên dương của cấp số nhân (u_n) thoả mãn 

A. 3        B. 2        C. 1        D. 0

Lời giải:

Đáp án: B

(do dãy trên có công bội nguyên dương)

Đáp án B.

Bài 20: Cho dãy số (un) với 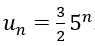. Khẳng định nào sau đây đúng?

A. (u_n) không phải là cấp số nhân.

B. (u_n) là cấp số nhân có công bội q = 5 và số hạng đầu u₁=3/2

C. (u_n) là cấp số nhân có công bội q = 5 và số hạng đầu u₁=15/2

D. (u_n) là cấp số nhân có công bội q = 2.5 và số hạng đầu u₁=3

Lời giải:

Đáp án: C

Vậy công bội q = 5, số hạng đầu là: 15/2.

Đáp án C.

Xem thêm các dạng bài tập toán hay khác:

300 Bài tập Toán 11 chương 3: Dãy số - Cấp số cộng và cấp số nhân (có đáp án năm 2023)

120 Bài tập về cấp số cộng (có đáp án năm 2023)

70 Bài tập về dãy số (có đáp án năm 2023)

60 Bài tập về phương pháp quy nạp toán học (có đáp án năm 2023)

70 Bài tập về phép thử và biến cố (có đáp án năm 2023)