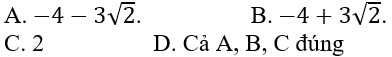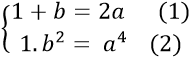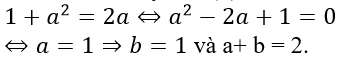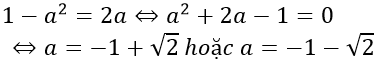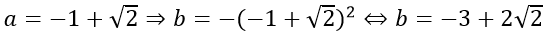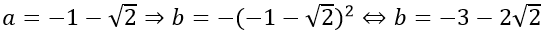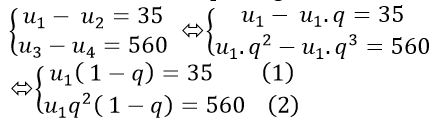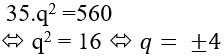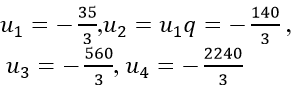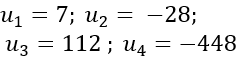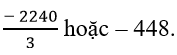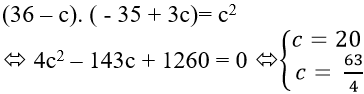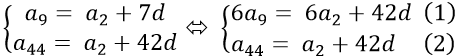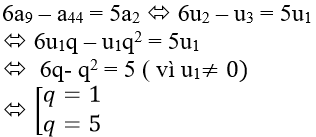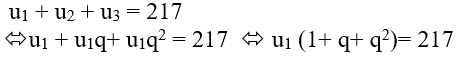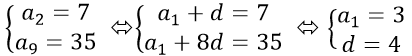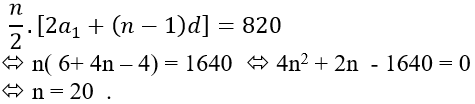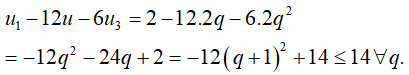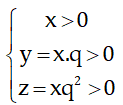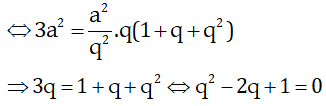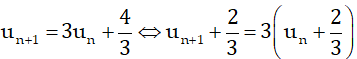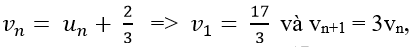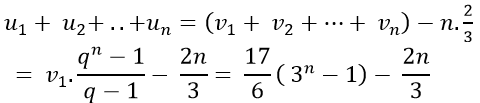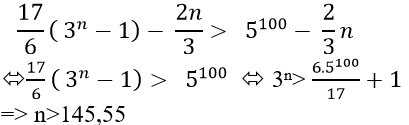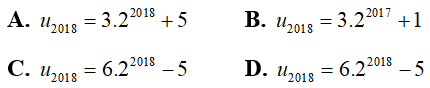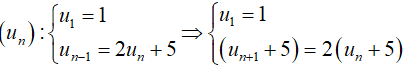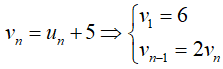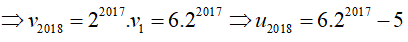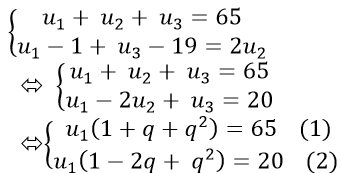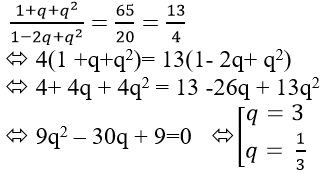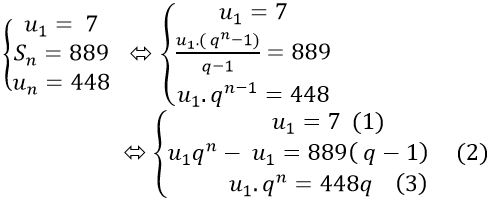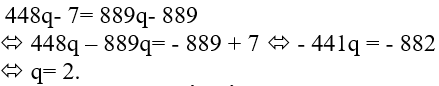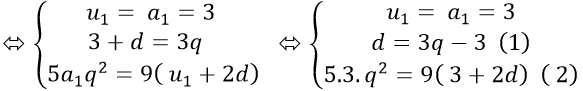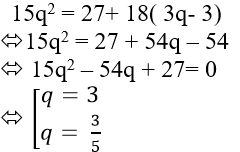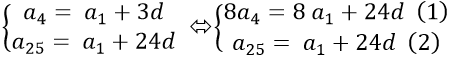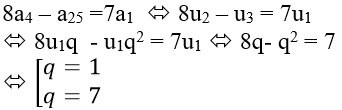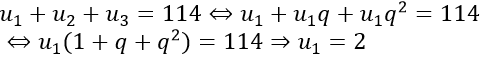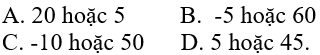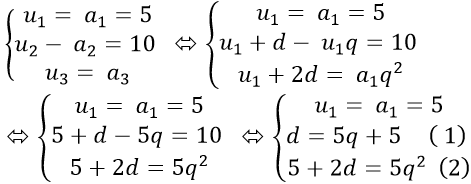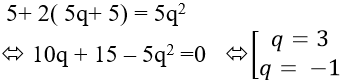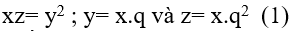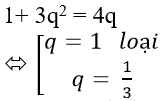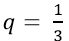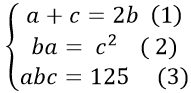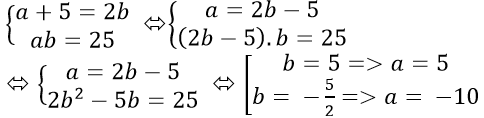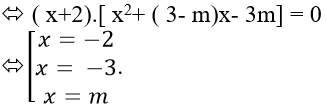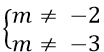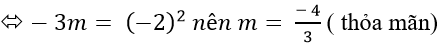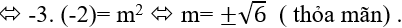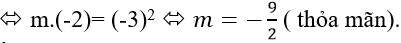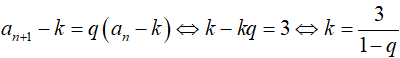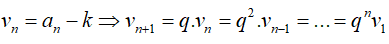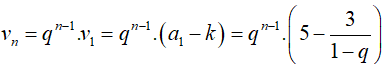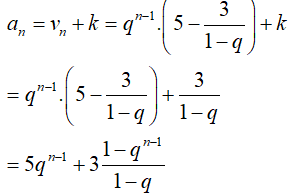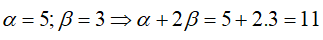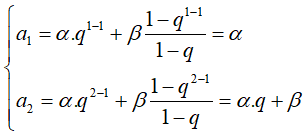20 Bài tập Cấp số nhân nâng cao (2024) có lời giải chi tiết nhất

Bài tập Cấp số nhân nâng cao có lời giải

Lý thuyết

1. Định nghĩa

- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.

Số q được gọi là công bội của cấp số nhân.

- Nếu (u_n) là cấp số nhân với công bội q, ta có công thức truy hồi:

u_{n + 1} = u_n. q với $n\in \mathbb{N}*$.

- Đặc biệt

Khi q = 0, cấp số nhân có dạng u₁, 0, 0, …., 0,…..

Khi q = 1, cấp số nhân có dạng u₁, u₁, u₁, …., u₁,…

Khi u₁ = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, 0, 0,…, 0..

- Ví dụ 1. Dãy số hữu hạn sau là một cấp số nhân: 2, 4, 8, 16, 32 với số hạng đầu u₁ = 2 và công bội q = 2.

2. Số hạng tổng quát

- Định lí: Nếu cấp số nhân có số hạng đầu u₁ và công bội q thì số hạng tổng quát u_n được xác định bởi công thức: u_n = u₁.q^{n - 1} với n ≥ 2.

- Ví dụ 2. Cho cấp số nhân (u_n) với u₁ = – 1; q = – 2.

a) Tính u₆;

b) Hỏi 128 là số hạng thứ mấy.

Lời giải:

a) Ta có: u₆ = u₁. q⁵ = –1. (– 2)⁵ = 32.

b) Ta có: u_n = u₁.q^{n - 1} nên 128 = – 1. (– 2)^{n - 1}

$\iff$(– 2)^{n - 1} = – 128 = (– 2)⁷.

$\iff$n – 1 = 7 nên n = 8.

Vậy 128 là số hạng thứ 8.

3. Tính chất các số hạng của cấp số nhân

- Định lí: Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:

$u_k^2=u_{k-1}.u_{k+\text{}1};k\ge 2$

( hay $\left|u_k\right|=\sqrt{u_{k-1}.u_{k+\text{}1}}$).

4. Tổng n số hạng đầu của một cấp số nhân

- Định lí: Cho cấp số nhân (u_n) với công bội q ≠ 1. Đặt S_n = u₁ + u₂ + …+ u_n .

Khi đó: $S_n=\frac{u_1(1-q^n)}{1-q}$.

- Chú ý: Nếu q = 1 thì cấp số nhân là u₁, u₁, u₁,….u₁,….Khi đó, S_n = n.u₁.

Ví dụ 3. Cho cấp số nhân (u_n) biết u₁ = 3; u₂ = 9. Tính tổng của 8 số hạng đầu tiên?

Lời giải:

Ta có: u₂ = u₁.q nên 9 = 3q.

Suy ra, công bội q = 3.

Khi đó, tổng của 8 số hạng đầu tiên là:

$$\begin{gathered} S_8=\frac{u_1(1-q^8)}{1-q} \\ =\frac{3.(1-3^8)}{1-3}=9840 \end{gathered}$$

Ví dụ minh họa

Ví dụ 1: Tìm a, b biết rằng 1,a,b là 3 số hạng liên tiếp của cấp số cộng và 1; a²; b² là 3 số hạng liên tiếp của một cấp số nhân .Tính a+ b?

Hướng dẫn giải:

Theo đề bài ta có hệ phương trình: 

Từ (2) suy ra: b = ± a²

* Với b = a² thay vào (1) được:

* Với b = −a² thay vào (1) được:

+ Nếu 

Khi đó: a + b = −4 + 3√2

+ Nếu 

Khi đó; a + b = −4 − 3√2

Chọn D.

Ví dụ 2: Cho bốn số hạng liên tiếp của một cấp số nhân, trong đó số hạng thứ hai nhỏ hơn số hạng thứ nhất 35, còn số hạng thứ ba lớn hơn số hạng thứ tư 560. Tìm số hạng thứ 4?

Hướng dẫn giải:

Theo đề bài ta có hệ phương trình: 

Thay (1) vào (2) ta được:

* Với q= 4 thay vào (1) được

* Với q= - 4 thay vào (1) ta được :

Vậy số hạng thứ tư của cấp số nhân là: 

Chọn D.

Ví dụ 3: Cho bốn số nguyên dương, trong đó ba số đầu lập thành một cấp số cộng, ba số hạng sau thành lập cấp số nhân. Biết rằng tổng của số hạng đầu và số hạng cuối là 37, tổng của hai số hạng giữa là 36. Tìm số hạng thứ tư.

Hướng dẫn giải:

Gọi bốn số nguyên dương cần tìm là: a, b, c, d.

* Theo đề bài có a, b, c là ba số hạng liên tiếp của cấp số cộng.

=> a + c = 2b (1)

* Ba số hạng b, c, d là ba số hạng liên tiếp của cấp số nhân.

=> bd = c² ( 2)

* Theo giả thiết ta có hệ phương trình:

* Từ (4) có: b= 36- c thay vào (1) được:

a+ c = 72- 2c ⇔ a = 72- 3c, thay a vào (3) được:

d = 37- 72 + 3c ⇔ d = - 35 + 3c.

* Thay b, d vào (2) được:

Với c = 20 => b = 16,a = 12,d = 95.

Với 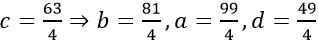 ( loại- vì bốn số đó là các số nguyên dương)

Chọn B.

Ví dụ 4: Ba số khác nhau có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân hoặc là các số hạng thứ 2 thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu tiên của cấp số cộng để tổng của chúng là 820?

Hướng dẫn giải:

Gọi u₁; u₂; u₃ là ba số hạng liên tiếp của cấp số nhân, với công bội là q.

Theo đề bài u₁ = a₂, u₂ = a₉ , u₃ = a₄₄ với a₂, a₉, a₄₄ là các số hạng của một cấp số cộng với công sai d.

Ta có

Lấy phương trình (1) – (2) được:

Vì u₁; u₂; u₃ khác nhau nên chọn q= 5..

Theo đề bài có:

Mà q = 5 => u₁ = 7

Suy ra u₂ = u₁q = 35.

Ta có

Theo đề bài ta có:S_n = 820 nên

Kết luận phải lấy 20 số hạng đầu tiên để tổng của chúng bằng 820.

Chọn A.

Ví dụ 5: Cho cấp số nhân (u_n) có u₁ = 2 và u₁ − 12u₂ − 6u₃ đạt giá trị lớn nhất. Tìm số hạng thứ 8 của cấp số nhân đã cho.

Hướng dẫn giải:

* Trước tiên ta đi tìm công bội của cấp số nhân.

Gọi q là công bội của cấp số nhân (u_n)

Ta có

Do đó để u₁ − 12u₂ − 6u₃ đạt giá trị lớn nhất thì q = -1.

* Số hạng thứ 8 của cấp số nhân đã cho là: u₈= u₁.q⁷ = 2.(-1)⁷ = - 2.

Chọn C .

Ví dụ 6: Tính các cạnh của 1 hình hộp chữ nhật; biết thể tích của nó là a³ ; diện tích toàn phần là 6a² và 3 cạnh lập thành cấp số nhân?

Hướng dẫn giải:

Gọi x;y;z là 3 canh của hình hộp chữ nhật.

Theo giả thiết ta có: 

V=xyz nên

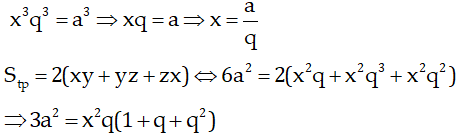
Do đó q = 1

Khi đó 3 cạnh của hình hộp chữ nhật là a;a;a.

Chọn D.

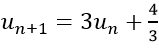
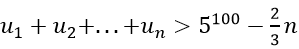
Ví dụ 7: Cho dãy số (u_n) thỏa mãn . Giá trị nhỏ nhất của n để  là

Hướng dẫn giải:

Ta có 

Đặt 

=> (v_n) là cấp số nhân với 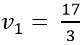 và công bội q= 3.

Suy ra:

Yêu cầu bài toán trở thành:

Vậy giá trị nhỏ nhất của n thỏa mãn bài toán là n = 146.

Chọn D.

Ví dụ 8: Cho dãy số (u_n) xác định bởi 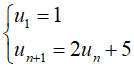.Tính số hạng thứ 2018 của dãy.

Hướng dẫn giải:

Ta có 

Đặt: 

Khi đó ta được dãy mới; là cấp số nhân với : v₁ = 6 và q = 2

Chọn D.

Bài tập trắc nghiệm

Câu 1: Cho ba số dương có tổng 65 lập thành một cấp số nhân tăng. Nếu bớt 1 đơn vị ở số hạng thứ nhất và 19 đơn vị ở số hạng thứ ba ta được một cấp số cộng. Tính tích của ba số đó?

Lời giải:

Đáp án: C

Gọi u₁; u₂; u₃ theo thứ tự lập thành một cấp số nhân.

Theo đề: u₁ − 1; u₂ ; u₃ − 19 theo thứ tự đó lập thành một cấp số cộng. Do đó, ta có hệ phương trình sau:

Lấy (1) chia (2) vế chia vế ta được

Vì u₁; u₂; u₃ theo thứ tự lập thành cấp số nhân tăng dần nên chọn q = 3 => u₁ = 5

Vậy u₁ = 5; u₂ = 15 và u₃ = 45 . Tích ba số đó là: 5.15.45= 3375.

Câu 2: Tìm công bội của một cấp số nhân có số hạng đầu là 7; số hạng cuối là 448 và tổng số các số hạng là 889.

Lời giải:

Đáp án: A

Theo đề bài ta có

Thế (3) vào (2) ta được : 448q − u₁ = 889(q − 1) (*)

Thay u₁ = 7 vào (*) ta được :

Vậy công bội của cấp số nhân là q = 2.

Câu 3: Một cấp số cộng và một cấp số nhân đều là các dãy tăng. Các số hạng thứ nhất của hai dãy số đều bằng 3; các số hạng thứ hai bằng nhau. Tỉ số giữa các số hạng thứ ba của cấp số nhân và cấp số cộng là 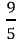. Tìm ba số hạng của cấp số nhân.

Lời giải:

Đáp án: C

Gọi u₁; u₂; u₃ là ba số hạng liên tiếp của cấp số cộng có công sai d.

Gọi a₁; a₂; a₃ là ba số hạng liên tiếp của cấp số nhân có công bội q.

Theo đề bài ta có hệ phương trình:

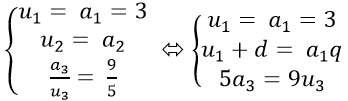
Ta có (2) ⇔ 15q² = 27 + 18d thay (1) vào ta được:

Vì cấp số nhân là dãy tăng nên ta chọn q = 3 .

=> ba số hạng của cấp số nhân là: 3; 9; 27.

Câu 4: Ba số khác nhau có tổng bằng 114 là ba số hạng liên tiếp của một cấp số nhân, hoặc coi là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng. Tìm số lớn nhất trong 3 số đó?

Lời giải:

Đáp án: C

Gọi u₁; u₂; u₃ là ba số hạng liên tiếp của cấp số nhân, với công bội là q.

Theo đề bài: u₁ = a₁, u₂ = a₄, u₃ = a₂₅, với a₁, a₄, a₂₅ là các số hạng của một cấp số cộng với công sai d.

Ta có: 

Lấy phương trình (1) – (2) được:

Vì u₁; u₂; u₃ khác nhau nên chọn q = 7.

Theo đề bài có:

Kết luận ba số cần tìm: u = 2, u₂ = 14, u₃ = 98.

Câu 5: Một cấp số cộng và cấp số nhân đều có số hạng đầu tiên là bằng 5, số hạng thứ hai của cấp số cộng lớn hơn số hạng thứ hai của cấp số nhân là 10, còn các số hạng thứ 3 của hai cấp số thì bằng nhau. Tìm số hạng thứ ba của cấp số nhân.

Lời giải:

Đáp án: D

Gọi u₁; u₂; u₃ là ba số hạng đầu tiên liên tiếp của cấp số cộng, với công sai d.

Gọi a₁; a₂; a₃ là ba số hạng đầu tiên liên tiếp của cấp số nhân, với công bội q.

Theo đề bài ta có:

Thế (1) vào (2) được:

* Với q = 3 => d = 20.

=> a₁ = 5; a₂= 15 và a₃ = 45.

Với q = -1 => a₁ = 5, a₂ = - 5, a₃ = 5.

Vậy số hạng thứ ba của cấp số nhân là 45 hoặc 5.

Câu 6: Ba số x, y, z theo thứ tự đó lập thành một cấp số nhân với công bội q (q ≠ 1), đồng thời các số x, 2y, 3z theo thứ tự đó lập thành một cấp số cộng với công sai d(d ≠ 0). Hãy tìm q?

Lời giải:

Đáp án: A

* Do ba số x, y,z theo thứ tự lập thành cấp số nhân nên:

* Do các số x, 2y, 3z theo thứ tự lập thành cấp số cộng nên ta có:

x + 3z = 2.2y thay (1) vào ta được:

x+ 3xq2 = 4xq mà x ≠ 0 nên:

Vậy công bội 

Câu 7: Cho a,b,c là ba số hạng liên tiếp của một cấp số cộng và b,c,a là ba số hạng liên tiếp của một cấp số nhân, đồng thời a.b.c= 125. Tính a. b

Lời giải:

Đáp án: D

* Do a,b, c là ba số hạng liên tiếp của cấp số cộng nên: a + c = 2b

* b,c, a là ba số hạng liên tiếp của một cấp số nhân, nên ba = c²

Ta có hệ phương trình: 

Thay (2) vào (3) được: c³ = 125 => c= 5

Thay c = 5 vào (1) và (2):

Vậy a= b= c= 5 hoặc a= - 10; 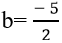;c=5

=> Tích a . b bằng 25.

Câu 8: Có bao nhiêu giá trị của m để phương trình: x³ + (5 − m)x² + (6 − 5m)x − 6m = 0 có 3 nghiệm phân biệt lập thành cấp số nhân ?

Lời giải:

Đáp án: C

* Ta có: x³ + (5 − m)x² + (6 − 5m)x − 6m = 0

* Để phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi:

* Do các nghiệm này lập thành cấp số nhân và ta sắp xếp các nghiệm này theo thứ tự tăng dần được các dãy số sau:

- 3; -2; m lập thành cấp số nhân 

- 3; m; - 2 lập thành cấp số nhân 

m; -3; - 2lập thành cấp số nhân 

Vậy có 4 giá trị của m thỏa mãn đầu bài.

Câu 9: Cho dãy số (a_n) xác định bởi a₁, a_{n + 1} = q.a_n + 3 với mọi n ≥ 1 trong đó q là hằng số, a ≠ 0, q ≠ 1. Biết công thức số hạng tổng quát của dãy số viết được dưới dạng 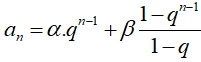 .Tính α + 2β

Lời giải:

Đáp án: C

Ta có: 

Đặt 

Khi đó 

Vậy

Do đó: 

Cách 2.

Theo giả thiết ta có a₁ = 5, a₂ = 5q + 3 Áp dụng công thức tổng quát, ta được 

Suy ra 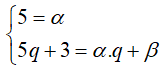 hay 

α + 2β = 5 + 2.3 = 11

Xem thêm các dạng bài tập toán hay khác:

300 Bài tập Toán 11 chương 3: Dãy số - Cấp số cộng và cấp số nhân (có đáp án năm 2024)

120 Bài tập về cấp số cộng (có đáp án năm 2024)

70 Bài tập về dãy số (có đáp án năm 2024)

Các công thức về Cấp số cộng, Cấp số nhân (2024) đầy đủ nhất

120 Bài tập về cấp số nhân (có đáp án năm 2024)