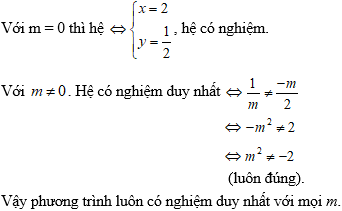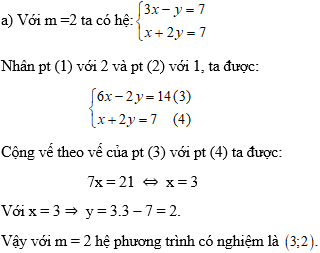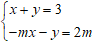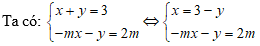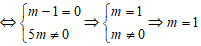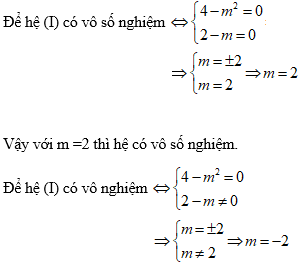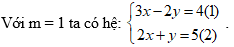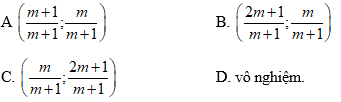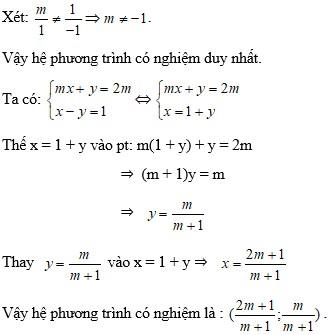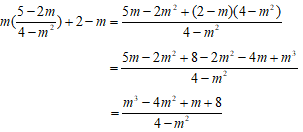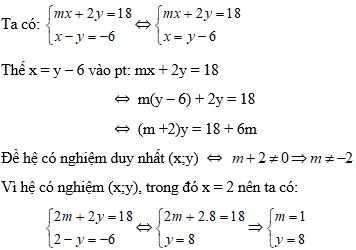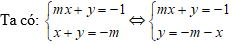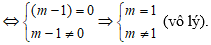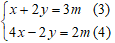30 Bài tập Cách giải hệ phương trình bậc nhất hai ẩn chứa tham số (2024) cực hay, có đáp án

Cách giải hệ phương trình bậc nhất hai ẩn chứa tham số 

1. Phương pháp giải

2. Ví dụ minh họa

Ví dụ 1: Cho hệ phương trình 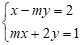. Tìm điều kiện của m để phương trình có nghiệm duy nhất.

Hướng dẫn:

Ví dụ 2: Cho hệ phương trình 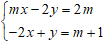. Tìm điều kiện của m để phương trình có nghiệm duy nhất và tìm nghiệm duy nhất đó.

Hướng dẫn:

Ví dụ 3: Cho hệ phương trình 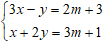 (m là tham số).

a) Giải hệ phương trình với m = 2.

b) Tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn x² + y² = 5.

Hướng dẫn:

3. Bài tập (có đáp án)

3.1. Bài tập trắc nghiệm

Cho hệ phương trình sau (I): 

Câu 1: Với m đạt giá trị nào để hệ phương trình có nghiệm duy nhất.

 A. m = 1

 B. m = –1

 C. m ≠ 1

 D. m ≠ 0

Lời giải:

Thế x = 3 – y vào pt: –m(3 – y) – y = 2m ⇒ (m -1)y = 5m (1)

Để hệ phương trình có nghiệm duy nhất ⇔ m -1 ≠ 0 ⇔ m ≠ 1.

Vậy với m ≠ 1 thì hệ phương trình (I) có nghiệm duy nhất.

Chọn đáp án C.

Câu 2: Với m đạt giá trị nào để hệ phương trình có vô số nghiệm.

 A. m = 1

 B. m = –1

 C. không có

 D. Mọi m nguyên dương

Lời giải:

Từ pt (1): Để hệ (I) có vô số nghiệm 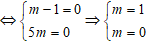 (vô lý).

Vậy không có giá trị nào của m thỏa mãn.

Chọn đáp án C.

Câu 3: Với m đạt giá trị nào để hệ phương trình vô nghiệm.

 A. m = 1

 B. m = –1

 C. m ≠ –1

 D. m ≠ 0

Lời giải:

Từ pt (1): Để hệ (I) vô nghiệm 

Vậy với m = 1 thì hệ phương trinh (I) vô nghiệm.

Chọn đáp án A.

Câu 4: Cho hệ phương trình sau: 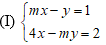. Khẳng định nào sau đây là không đúng?

 A. Hệ phương trình (I) có nghiệm duy nhất khi m ≠ ±2.

 B. Hệ phương trình (I) có vô số nghiệm khi m = 2.

 C. Hệ phương trình (I) vô nghiệm khi m = –2

 D. khẳng định A, B sai.

Lời giải:

Ta có:

Thế y = mx – 1 vào pt: 4x – my = 2 ⇒ 4x – m(mx – 1) = 2 ⇔ (4 – m²)x = 2 – m (1).

Để hệ (I) có nghiệm duy nhất (4 - m²) ≠ 0 ⇒ m² ≠ 4⇒m ≠ ±2.

Vậy với m ≠ ±2 thì hệ có nghiệm duy nhất.

Vậy với m = –2 thì hệ vô nghiệm.

Chọn đáp án D.

Câu 5: Cho hệ phương trình sau: 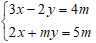. Với m = 1 thì hệ có nghiệm là?

 A. (x;y) = (2;1)

 B. (x;y) = (1;2)

 C. (x;y) = (2;–1)

 D. (x;y) = (1;1)

Lời giải:

Từ pt (2) ⇒ y = 5 – 2x.

3x – 2(5 – 2x) = 4 ⇔ 3x + 4x – 10 = 4 ⇔ 7x = 14 ⇔ x = 2.

Với x = 2 thì y = 5 – 2.2 = 1.

Vậy nghiệm của hệ phương trình là (x;y) = (2;1).

Chọn đáp án A.

Câu 6: Cho hệ phương trình sau: 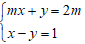 có nghiệm là?

Lời giải:

Chọn đáp án B.

Câu 7: Cho hệ phương trình sau: 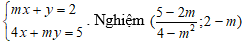 có là nghiệm của hệ phương trình không?

 A. Có

 B. Không.

Lời giải:

Thay 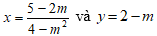 vào vế trái phương trình (1) ta được:

Mà vế phải của phương trình (1) bằng 2. Do đó vế trái và vế phải của phương trình (1) khác nhau, hay 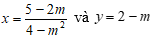 không phải là nghiệm của hệ phương trình.

Vậy Nghiệm không phải là nghiệm của hệ phương trình.

Chọn đáp án B.

Câu 8: Cho hệ phương trình sau: 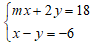. Với giá trị nào của m để hệ có nghiệm (x;y) trong đó x = 2.

 A. m = 1

 B. m = 2

 C. m = 4

 D. m = 5

Lời giải:

Vậy m = 1.

Chọn đáp án A.

Câu 9: Cho hệ phương trình sau: 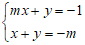. Bạn Nam nói hệ có nghiệm duy nhất khi m ≠ ±1, và bạn Tùng nói không có giá trị nào của m thỏa mãn để hệ vô nghiệm. Nam và Tùng nói đúng hay sai?

 A. Cả hai bạn Nam và Tùng đều sai.

 B. Cả hai bạn Nam và Tùng đều đúng.

 C. Bạn Nam sai, bạn Tùng đúng.

 D. bạn Nam đúng, bạn Tùng sai.

Lời giải:

Thay y = –m – x vào pt (1) ta được: mx + (–m – x) = – 1 ⇔ (m – 1)x = m – 1

Để hệ phương trình có nghiệm duy nhất ⇔(m-1) ≠ 0⇒m ≠ 1

Vậy với m ≠ 1 thì hệ có nghiệm duy nhất.

Để hệ phương trình vô nghiệm 

Vậy không có giá nào của m để hệ vô nghiệm.

Vậy bạn Nam trả lời sai, bạn Tùng trả lời đúng.

Chọn đáp án C.

Câu 10: Cho hệ phương trình: . Nghiệm nào sau đây là nghiệm của hệ phương trình?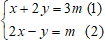

 A. (m;m).

 B. (m – 1;m)

 C. (m;m – 1)

 D. (- m;- m)

Lời giải:

Vì 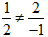 nên hệ phương trình có nghiệm duy nhất.

Nhân pt (1) với 1 và pt (2) với 2, ta được: 

Cộng vế theo vế của pt (3) và pt (4) ta được: 5x = 5m ⇔ x = m.

Với x = m ⇒ y = 2m – m = m.

Vậy nghiệm của hệ phương trình là: (m;m).

Chọn đáp án A.

3.2. Bài tập tự luyện 

Bài 1: Cho hệ phương trình $\left\{\begin{array}{l}mx+3y=6\\ x+2y=4\end{array}\right.$ (m là tham số). Tìm điều kiện của m để hệ phương trình vô số nghiệm.

Bài 2:  Cho hệ phương trình $\left\{\begin{array}{l}2mx-5y=-2\\ 5x-2my=3-2m\end{array}\right.$ (m là tham số)

a) Tìm m để hẹ phương trình có nghiệm duy nhất.

b) Tìm m nguyên để nghiệm duy nhất (x; y) sao cho x; y nguyên.

Bài 3: Cho hệ phương trình $\left\{\begin{array}{l}mx-y=2m\\ 4x-my=m+6\end{array}\right.$ (m là tham số)

a) Giải phương trình khi m = 1.

b) Giải và biện luận hệ phương trình đã cho theo m.

Bài 4: Cho hệ phương trình $\left\{\begin{array}{l}2mx+y=2\\ x+2my=4-4m\end{array}\right.$ (m là tham số)

a) Tìm m để hệ phương trình có nghiệm duy nhất.

b) Tìm các giá trị nguyên của m sao cho hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x nguyên; y nguyên.

Bài 5: Cho hệ phương trình $\left\{\begin{array}{l}mx+y=3\\ 4x+my=6\end{array}\right.$ (m là tham số)

Tìm điều kiện của m để hệ phương trình có nghiệm duy nhât (x; y) thỏa mãn x > 2; y > 0.

Bài 6: Cho hệ phương trình $\left\{\begin{array}{l}-2mx+y=5\\ mx+3y=1\end{array}\right.$ (m là tham số)

a) Giải hệ phương trình khi m = 1.

b) Tìm các giá trị của tham số m để hệ phương trình có nghiệm (x; y) thỏa mãn x – y = 2.

Bài 7: Cho hệ phương trình $\left\{\begin{array}{l}x-my=0\\ mx-y=m+1\end{array}\right.$ (với m là tham số)

Tìm hệ thức liên hệ giữa x và y không phụ thuộc vào m.

Bài 8: Cho hệ phương trình $\left\{\begin{array}{l}2x+4y=m+3\\ x-y=m+1\end{array}\right.$ (với m là tham số)

Tìm hệ thức liên hệ giữa x và y không phụ thuộc vào tham số m.

Bài 9: Cho hệ phương trình $\left\{\begin{array}{l}2mx+4y=3\\ x-2y=m+1\end{array}\right.$ (với m là tham số)

Tìm m để 2x – 3y = 0.

Bài 10: Cho hệ phương trình $\left\{\begin{array}{l}2mx+y=2\\ 8x+my=m+2\end{array}\right.$ (với m là tham số)

a) Giải hệ phương trình khi m = -1.

b) Tìm m để hệ phương trình có nghiệm (x; y) = (2; -6).

c) Giải và biện luận hệ phương trình theo m.

d) Tìm hệ thức liên hệ giữa x và y không phụ thuộc vào m.

e) Tìm m để 4x + 3y = 7

f) Tìm m để x – y > 0.

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

50 Bài tập Giải hệ phương trình bằng phương pháp thế (có đáp án năm 2023)

50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2023)

50 Bài tập Phương trình bậc hai một ẩn (có đáp án năm 2023)

50 Bài tập Công thức nghiệm thu gọn (có đáp án năm 2023)

50 Bài tập Hệ thức Vi – ét và ứng dụng (có đáp án năm 2023)