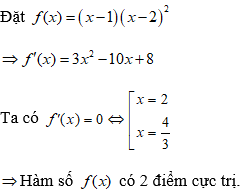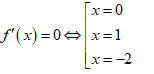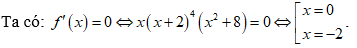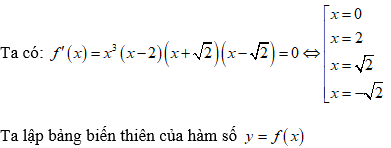30 Bài tập về đạo hàm trị tuyệt đối (2024) có đáp án

30 Bài tập về đạo hàm trị tuyệt đối

I. Phương pháp giải

Ta sử dụng công thức đạo hàm theo định nghĩa để tính đạo hàm của hàm số y = |x|.

$\underset{∆x\to \infty }{\lim }\frac{f(x+∆x)-x}{∆x}$Khi thay giá trị |x| vào, đạo hàm trị tuyệt đối của x là:

$y\text{'}=\underset{∆x\to \infty }{\lim }\frac{\left|x+∆x\right|-\left|x\right|}{∆x}$

Nhìn vào công thức đạo hàm ở trên, các em thấy rằng đạo hàm sẽ không xác định được tại vị trí ∆x = 0, bởi vì hàm số y = |x| là hàm số không liên tục và có dạng:

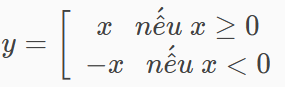
Đồ thị hàm số y = |x| khi vẽ sẽ giúp các em thấy rõ hơn.

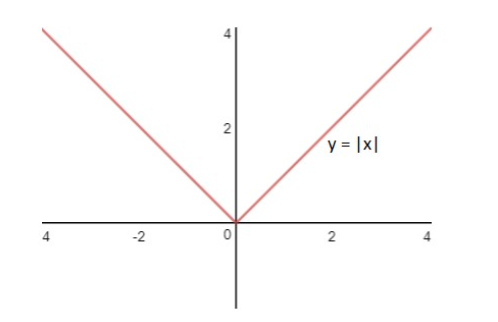
Do đó, chúng ta không thể thay trực tiếp ∆x = 0 vào (1) để tính được, mà ta cần biến đổi thành dạng khác để mẫu khác 0 khi thay ∆x = 0 vào. Các em có thể làm như sau:

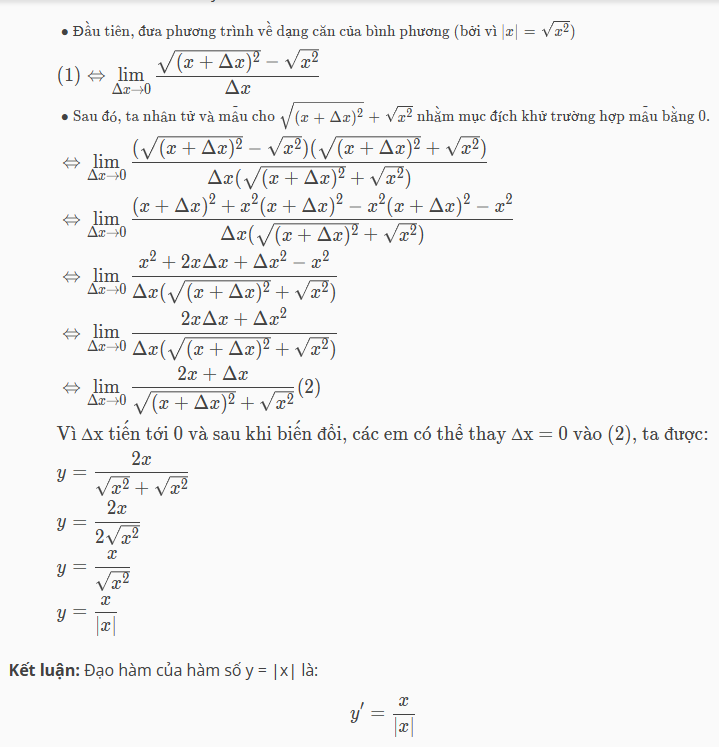
Để tính nhanh đạo hàm trị tuyệt đối, các em cần ghi nhớ một số công thức tính nhanh đạo hàm có thể kể đến như:

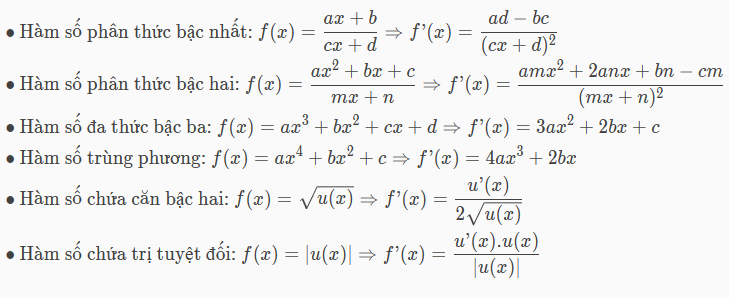
Ví dụ:

Hoặc 

Trong đó:

• Số gia của đối số là: ∆x=x – x0

• Số gia của hàm số là: ∆y=y – y0

Dựa vào công thức đạo hàm ban đầu, ta sẽ bắt đầu tính hàm số y = |x|

Thay giá trị |x| vào, ta sẽ tính đạo đạo hàm của y' bằng cách:

Nhìn vào công thức đạo hàm ở trên, các em thấy rằng đạo hàm sẽ không xác định được tại vị trí ∆x=0, bởi vì hàm số y=|x| là 1 hàm số không liên tục và có dạng:

• y= x nếu x >= 0

• y= -x nếu x < 0

Nhìn vào đồ thị y = |x| sẽ giúp bạn đọc dễ hình dung vị trí của y = |x| và xác định đúng giá của của |x|.

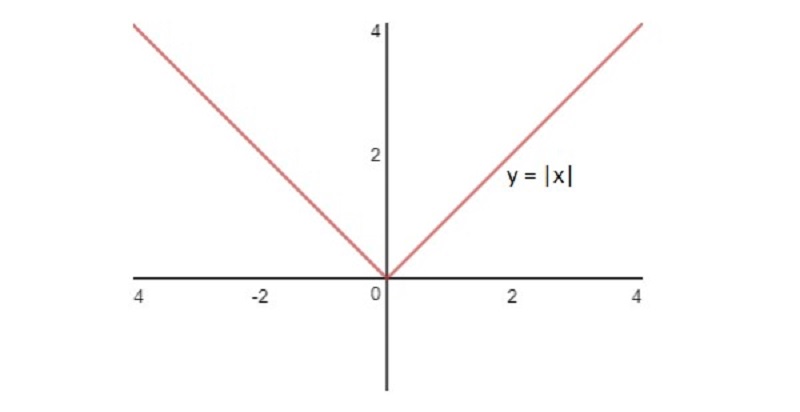
II. Bài tập vận dụng

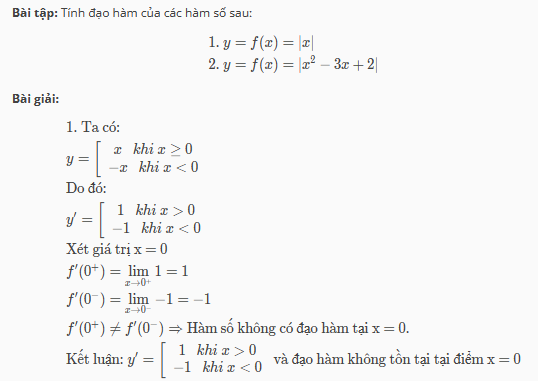
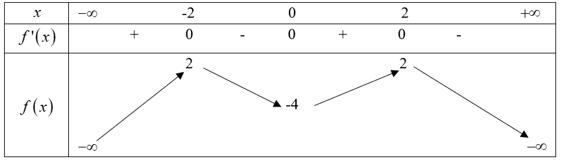
3: Cho hàm số y = f(x) có bảng biến thiên như sau. Đồ thị hàm số y = |f(x)| có bao nhiêu điểm cực trị?

A. 5.

B. 6.

C. 3.

D. 7.

Lời giải

Chọn D

Đồ thị hàm y = |f(x)| gồm 2 phần.

+ Phần đồ thị y = f(x) nằm trên Ox

+ Phần đồ thị lấy đối xứng qua Ox của đồ thị y = f(x) nằm dưới Ox

Đồ thị hàm số y = f(x) giao với trục Ox tại các điểm có hoành độ x₁; x₂; x₃; x₄

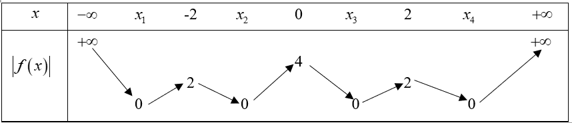
Từ đó ta có bảng biến thiên của y = |f(x)|

Từ bảng biến thiên này hàm số y = |f(x)| có 7 điểm cực trị.

4: Cho hàm số y = |(x - 1)(x - 2)²|. Số điểm cực trị của hàm số là:

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải

Chọn C

Mặt khác phương trình f(x) = (x - 1)(x - 2)² = 0 có 1 nghiệm đơn x = 1

Ta có số điểm cực trị của hàm số y = |(x - 1)(x - 2)²| là tổng số điểm cực trị của hàm số f(x) = (x - 1)(x - 2)² và số nghiệm bội lẻ của phương trình f(x) = 0.

Vậy số điểm cực trị của hàm số y = |(x - 1)(x - 2)²| là 3

5: Cho hàm số 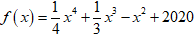, số điểm cực trị của hàm số y = f(|x|) là

A. 2.

B. 3.

C. 4.

D. 5.

Lời giải:

Chọn B

Số điểm cực trị dương của hàm số y = f(x) là n thì số điểm cực trị của hàm số y = f(|x|) là 2n + 1

Ta có f'(x) = x³ + x² - 2x = x(x - 1)(x + 2)

Hàm số y = f(x) có một điểm cực trị dương nên hàm số y = f(|x|) có 3 điểm cực trị.

6: Cho hàm số y = f(x) có đạo hàm f'(x) = x(x + 2)⁴ (x²+8). Số điểm cực trị của hàm số y = f(|x|) là:

A. 0.

B. 1.

C. 2.

D. 3.

Lời giải:

Chọn B

Do f'(x)chỉ đổi dấu khi đi qua điểm x = 0 nên hàm số f(x) có 1 điểm cực trị x = 0.

Số điểm cực trị dương của hàm số y = f(x) là n thì số điểm cực trị của hàm số y = f(|x|) là 2n + 1

Do đó hàm y = f(|x|) có duy nhất 1 điểm cực trị.

7: Cho hàm số y = f(x) có đạo hàm f'(x) = (x³ - 2x²)(x³ - 2x). Hàm số y = |f(x)| có nhiều nhất bao nhiêu điểm cực trị?

A. 9.

B. 8.

C. 7.

D. 6.

Lời giải:

Chọn A

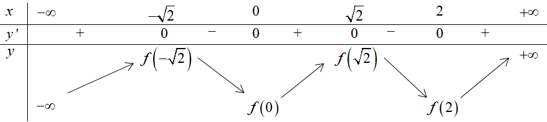
Từ bảng biến thiên ta thấy hàm số y = f(x) có 4 điểm cực trị, suy ra f(x) = 0 có tối đa 5 nghiệm phân biệt.

Do đó hàm số y = |f(x)| có tối đa 4 + 5 = 9 điểm cực trị.

8: Cho hàm số y = f(x) xác định và liên tục trên R, có bảng xét dấu của f'(x) như sau

Số điểm cực trị của đồ thị hàm số y = f(|x - 2|) + 2020 là:

A. 5.

B. 4.

C. 0.

D. 3.

Lời giải:

Chọn A

Xét hàm số .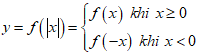

Khi đó ta có bảng xét dấu của hàm số y = f(|x|) như sau

Suy ra đồ thị hàm số y = f(|x|) có 5 điểm cực trị.

Suy ra đồ thị hàm số y = f(|x - 2|) có 5 cực trị (Tịnh tiến đồ thị hàm số y = f(|x|) sang phải 2 đơn vị thì số điểm cực trị không thay đổi).

Suy ra đồ thị hàm số y = f(|x - 2|) + 2020 có 5 cực trị (Tịnh tiến đồ thị hàm số y = f(|x - 2|) lên trên 2020 đơn vị thì số điểm cực trị không thay đổi).

Xem thêm các dạng bài tập hay, có đáp án:

30 Bài tập Tìm cực trị của hàm chứa dấu giá trị tuyệt đối (2024) cực hay, có lời giải

20 Bài tập Tính đạo hàm chứa dấu giá trị tuyệt đối (2024) chi tiết, có đáp án

20 Bài tập Cách tính giới hạn của hàm số có chứa trị tuyệt đối (2024) cực hay, có đáp án chi tiết

30 Bài tập Vẽ đồ thị hàm số chứa dấu giá trị tuyệt đối (2024) hay, có đáp án chi tiết

50 Bài tập Cách tính đạo hàm của hàm số có chứa trị tuyệt đối (2024) cực hay, có đáp án chi tiết