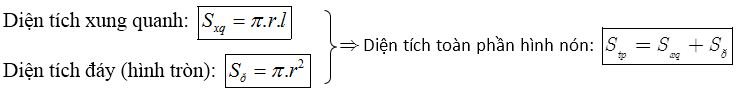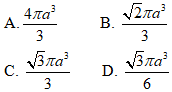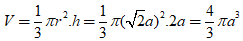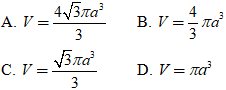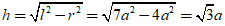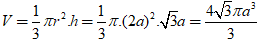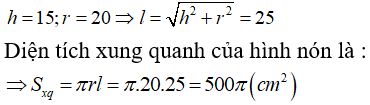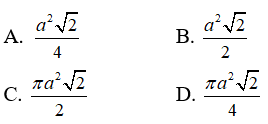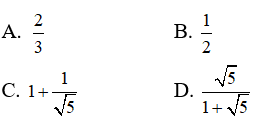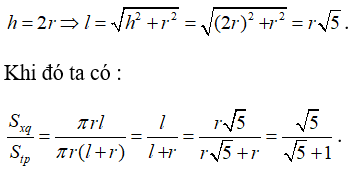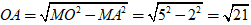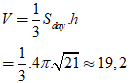Bài tập về các công thức tính mặt tròn xoay

I. Lý thuyết

A. MẶT NÓN

1. Mặt nón tròn xoay

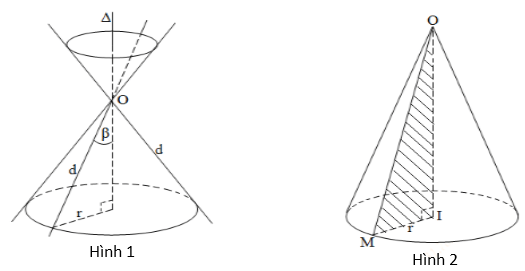
    Trong mặt phẳng (P), cho 2 đường thẳng d, Δ cắt nhau tại O và chúng tạo thành góc β với 0^o < β ≤ 90^o . Khi quay mp(P) xung quanh trục Δ với góc β không thay đổi được gọi là mặt nón tròn xoay đỉnh O (hình 1).

    - Người ta thường gọi tắt mặt nón tròn xoay là mặt nón.

    - Đường thẳng Δ gọi là trục, đường thẳng d được gọi là đường sinh và góc 2β gọi là góc ở đỉnh.

2. Hình nón tròn xoay

    Cho ΔOIM vuông tại I quay quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình, gọi là hình nón tròn xoay (gọi tắt là hình nón) (hình 2).

    - Đường thẳng OI gọi là trục, O là đỉnh, OI gọi là đường cao và OM gọi là đường sinh của hình nón.

    - Hình tròn tâm I, bán kính r = IM là đáy của hình nón.

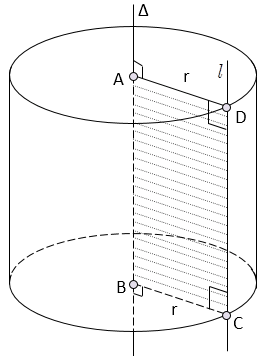
3. Công thức diện tích hình nón và thể tích khối nón

    Cho hình nón có chiều cao là h, bán kính đáy r và đường sinh là l thì có:

    - Thể tích khối nón: .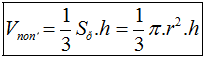

4. Tính chất:

    - TH1: Nếu cắt mặt nón tròn xoay bởi mp(P) đi qua đỉnh thì có các trường hợp sau xảy ra:

        + Nếu mp(P) cắt mặt nón theo 2 đường sinh ⇒ Thiết diện là tam giác cân.

        + Nếu mp(P) tiếp xúc với mặt nón theo một đường sinh. Trong trường hợp này, người ta gọi đó là mặt phẳng tiếp diện của mặt nón.

    - TH2: Nếu cắt mặt nón tròn xoay bởi mp(Q) không đi qua đỉnh thì có các trường hợp sau xảy ra:

        + Nếu mp(Q) vuông góc với trục hình nón ⇒ giao tuyến là một đường tròn.

        + Nếu mp(Q) song song với 2 đường sinh hình nón giao tuyến là 2 nhánh của 1 hypebol.

        + Nếu mp(Q) song song với 1 đường sinh hình nón giao tuyến là 1 đường parabol.

B. MẶT TRỤ

1. Mặt trụ tròn xoay

    Trong mp(P) cho hai đường thẳng Δ và l song song nhau, cách nhau một khoảng r. Khi quay mp(P) quanh trục cố định Δ thì đường thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay hay gọi tắt là mặt trụ.

    - Đường thẳng Δ được gọi là trục.

    - Đường thẳng l được gọi là đường sinh.

    - Khoảng cách r được gọi là bán kính của mặt trụ.

2. Hình trụ tròn xoay

    Khi quay hình chữ nhật ABCD xung quanh đường thẳng chứa một cạnh, chẳng hạn cạnh AB thì đường gấp khúc ABCD tạo thành một hình, hình đó được gọi là hình trụ tròn xoay hay gọi tắt là hình trụ.

    - Đường thẳng AB được gọi là trục.

    - Đoạn thẳng CD được gọi là đường sinh.

    - Độ dài đoạn thẳng AB = CD = h được gọi là chiều cao của hình trụ.

    - Hình tròn tâm A, bán kính r = AD và hình tròn tâm B, bán kính r = BC được gọi là 2 đáy của hình trụ.

    - Khối trụ tròn xoay, gọi tắt là khối trụ, là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ.

3. Công thức tính diện tích hình trụ và thể tích khối trụ

    Cho hình trụ có chiều cao là và bán kính đáy bằng r, khi đó:

    - Diện tích xung quanh của hình trụ: S_xq = 2πrh

    - Diện tích toàn phần của hình trụ: S_tp = S_xq + 2.S_Đay = 2πrh + 2πr²

    - Thể tích khối trụ: V = B.h = πr²h

4. Tính chất:

    - Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mp(α) vuông góc với trục Δ thì ta được đường tròn có tâm trên α và có bán kính bằng r với r cũng chính là bán kính của mặt trụ đó.

    - Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mp(α) không vuông góc với trục Δ nhưng cắt tất cả các đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng 2r và trục lớn bằng 2r/sinφ, trong đó φ là góc giữa trục Δ và mp(α) với 0⁰ < φ < 90⁰.

    - Cho mp(α) song song với trục Δ của mặt trụ tròn xoay và cách Δ một khoảng d.

        + Nếu d < r thì mp(α) cắt mặt trụ theo hai đường sinh ⇒ thiết diện là hình chữ nhật.

        + Nếu d = r thì mp(α) tiếp xúc với mặt trụ theo một đường sinh.

        + Nếu d > r thì mp(α) không cắt mặt trụ

II. Ví dụ minh họa

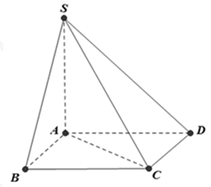
Ví dụ 1 Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy SC = a√6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:

Hướng dẫn giải:

+ Do ABCD là hình vuông cạnh a nên AC = a√2

+ Xét tam giác SAC có:
SA = 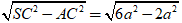 = 2a

+ Hình nón tròn xoay được tạo thành có bán kính đường tròn đáy r = AC = a√2 ; đường cao SA = 2a. Do đó, thể tích hình nón là:

Chọn A.

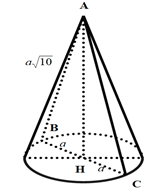
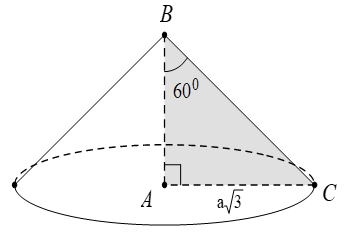
Ví dụ 2 Trong không gian, cho tam giác ABC cân tại A, AB = a√7 ; BC = 4a. Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH.

Hướng dẫn giải:

Do tam giác ABC là tam giác cân tại A có AH là đường trung tuyến nên AH ⊥ BC

Khi quay tam giác ABC xung quanh trục AH ta được hình nón có:

+ Đường sinh l = AB = a√7

+ Bán kính đáy r = 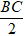 = 2a

Suy ra đường cao của hình nón là:

+ Thể tích của hình nón tạo thành là:

Chọn A.

III. Bài tập vận dụng

Câu 1: Hình nón (N) có đường sinh gấp hai lần đường cao. Góc ở đỉnh của hình nón là:

A. 120^o    

B. 90^o   

C. 60^o    

D. 30^o

Lời giải:

Gọi 2α là góc ở đỉnh của hình nón. Từ giả thiết ta có:

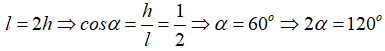
Câu 2: Hình nón có chiều cao bằng $\frac{4}{3}$ bán kính đáy. Tỉ số giữa diện tích toàn phần và diện tích xung quanh của hình nón là:

A. $\frac{4}{3}$   

B. $\frac{5}{7}$   

C. $\frac{8}{5}$ 

D. $\frac{9}{5}$

Lời giải:

Từ giả thiết ta có

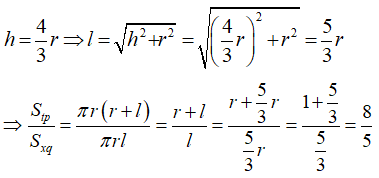
Câu 3: Hình nón có góc ở đỉnh là 90^o và có diện tích xung quanh là π$\sqrt{2}$ . Độ dài đường cao của hình nón là:

A. 1   

B. $\sqrt{2}$ 

C. $\frac{1}{\sqrt{2}}$    

D. 2

Câu 4: Cho hình nón tròn xoay có đường cao h=15cm và bán kính đáy r = 20cm. Diện tích xung quanh của hình nón là:

A. 1000π(cm²)   

B. 250π(cm²)    

C. 375π(cm²)   

D. 500π(cm²)

Câu 5: Tam giác ABC vuông cân đỉnh A có cạnh huyền là a. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo thành hình nón (N). Diện tích xung quanh của hình nón (N) là:

Lời giải:

Theo cách xây dựng hình nón ta có đường sinh của hình nón là: l = BC = a .

Bán kính đáy của hình nón là: r = AC = BC.sin45^o = $\frac{a}{\sqrt{2}}$

Vậy ta có diện tích xung quanh của hình nón (N) là:

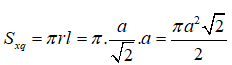
Đáp án đúng là C.

Câu 6: Hình nón (N) có đường sinh gấp hai lần bán kính đáy. Góc ở đỉnh của hình nón là :

A. 120^o    

B. 60^o   

C. 30^o   

D. 0^o

Lời giải:

Từ giả thiết ta có l = 2r .

Gọi 2α là góc ở đỉnh của hình nón, khi đó ta có :

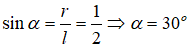
Vậy góc ở đỉnh của hình nón là 60^o .

Đáp án đúng là B.

Câu 7: Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón bằng :

Câu 8: Một chiếc phễu đựng dầu hình nón có chiều cao là 30cm và đường sinh là 50cm. Giả sử rằng lượng dầu mà chiếc phễu đựng được chính là thể tích của khối nón. Khi đó trong các lượng dầu sau đây, lượng dầu nào lớn nhất chiếc phễu có thể đựng được :

A. 150720π(cm³)   

B. 50400π(cm³)

C. 16000π(cm³)   

D. 12000π(cm³)

Lời giải:

Từ giả thiết ta có h = 30cm ; l = 50cm. Khi đó ta có

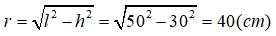
Thể tích khối nón là :

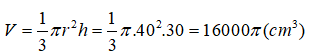
Đáp án đúng là C.

Câu 9: Cho hình trụ có được khi quay hình chữ nhật ABCD quanh trục AB. Biết rằng AB = 2AD = 2a. Thể tích khối trụ đã cho theo a là 

A. 2πa³   

B.πa³   

C. $\frac{2\pi a^3}{3}$ 

D.$\frac{\pi a^3}{2}$

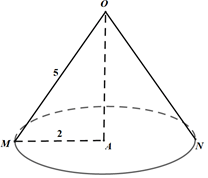
Câu 10: Cho một hình cầu bán kính 5, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo thành là một đường kính 4. Tính thể tích của khối nón có đáy là thiết diện vừa tạo và đỉnh là tâm hình cầu đã cho. ( kết quả làm tròn tới hàng phần trăm).

A.18,18    B. 19,19    C. 19,2.    D. 17,16

Hướng dẫn giải:

Gọi thiết diện là đường tròn tâm A, đường kính d= 4 ⇒ bán kính r = 2. Gọi MN là một đường kính của đường tròn (A).

Gọi O là tâm của mặt cầu đã cho.

Hình nón có đáy là thiết diện là hình tròn tâm A và đỉnh là O có:

• Bán kính đường tròn đáy là: r = 2.

• Đường sinh là OM = 5 ( = bán kính của hình cầu đã cho)

• Chiều cao:

Diện tích đường tròn đáy là: S = πr² = 4π

Thể tích khối nón cần tính là:

Chọn C

Xem thêm các dạng câu hỏi và bài tập liên quan khác:

20 bài tập về Hình chữ nhật, Hình thoi, Hình bình hành, Hình thang cân (2024) có đáp án, chi tiết nhất 

60 Bài tập khái niệm về mặt tròn xoay (có đáp án năm 2023) - Toán 12 

30 bài tập Tam giác đều. Hình vuông. Lục giác đều (2024) hay nhất, có đáp án 

Công thức diện tích toàn phần hình trụ (2024) chi tiết nhất 

30 Bài tập về tính chu vi, diện tích hình vuông (2024) có đáp án