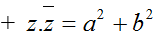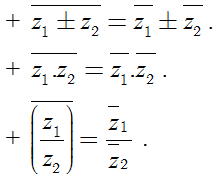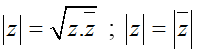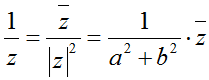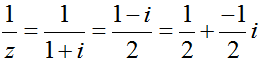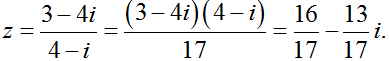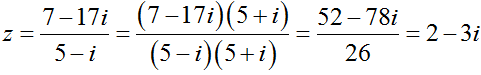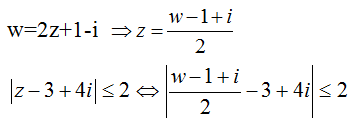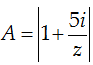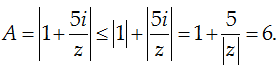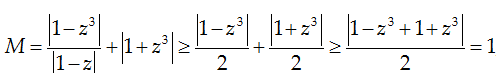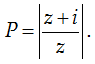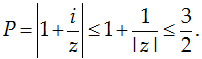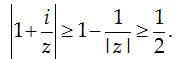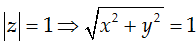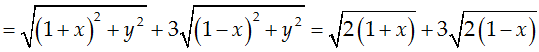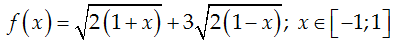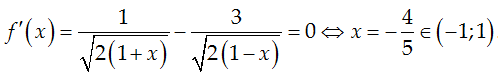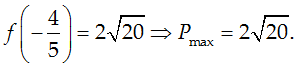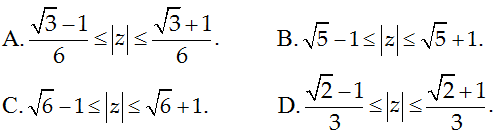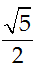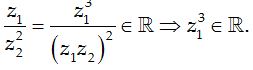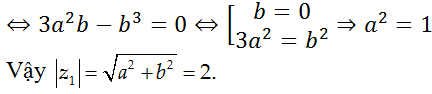Bài tập về bình phương số phức
I. Lý thuyết
1. Phần thực và phần ảo của số phức, số phức liên hợp.
a) Số phức z là biểu thức có dạng z = a + bi (a, b ∈ R, i2 = -1) . Khi đó:
+ Phần thực của z là a, phần ảo của z là b và i được gọi là đơn vị ảo.
b) Số phức liên hợp của z là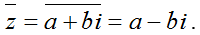 
.
+ Tổng và tích của z và z− luôn là một số thực.
Đặc biệt:
+ Số phức z = a + 0i có phần ảo bằng 0 được coi là số thực và viết là z = a
+ Số phức z = 0 + bi có phần thực bằng 0 được gọi là số ảo (hay số thần ảo) và viết là
+ Số i = 0 + li = li.
+ Số: 0 = 0 + 0i vừa là số thực vừa là số ảo.
2. Số phức bằng nhau.
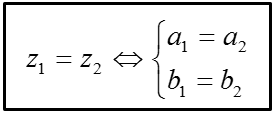
+ Cho hai số phức z1 = a1 + b1i, z2 + b2i (a1, a2, b1, b2 ∈ R). Khi đó:
3. Biểu diễn hình học của số phức, mô đun của số phức.
a) Biễu diễn hình học của số phức.
+ Số phức z = a + bi (a, b ∈ R) được biểu diễn bởi điểm M(a; b) trong mặt phẳng tọa độ.
+ z và z− được biểu diễn bởi hai điểm đối xứng nhau qua trục 0x.
b) Mô đun của số phức.
+ Mô đun của số phức z là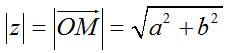 
.
+ 
4. Cộng, trừ và nhân số phức
Cho hai số phức z1 = a + bi và z2 = c + di thì:
• Phép cộng số phức: z1 + z2 = (a + c) + (b + d)i
• Phép trừ số phức: z1 - z2 = (a - c) + (b - d)i
- Mọi số phức z = a + bi thì số đối của z là -z = -a - bi: z + (-z) = (-z) + z = 0
• Phép nhân số phức: z1.z2 = (ac - bd) + (ad + bc)i
• Phép chia số phức: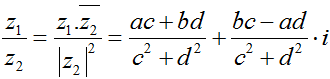
(với z2 ≠ 0)
- Chú ý :
• Với mọi số thực k và mọi số phức z = a + bi thì:
k(a + b)i = ka + kbi
• Với mọi số phức: 0z = 0
• Phép cộng và phép nhân các số phức có tất cả các tính chất của phép cộng và phép nhân của số thực.
• i4k = 1; i4k + 1 = i; i4k + 2 = -1; i4k + 3 = -i
5. Phép chia số phức
Cho hai số phức z1 = a + bi và z2 = c + di thì:
- Số phức nghịch đảo của z = a + bi ≠ 0: 
- 
(với z2 ≠ 0)
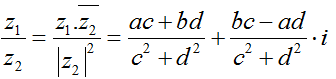
II. Ví dụ minh họa
Ví dụ 1: Cho số phức z = 2 + 5i . Tìm số phức w = iz + z−.
A. w = 7 - 3i. B. w = -3 - 3i. C. w = 3 = 3i. D. w = -7 - 7i.
Lời giải:
Ta có: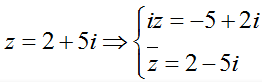 
⇔ w = iz + z− = (-5 + 2) + (2 - 5)i = -3 - 3i.
Vậy chọn đáp án B.
Ví dụ 2: Cho số phức z = (1 - 6i) - (2 - 4i). Phần thực, phần ảo của z lần lượt là
A. -1; -2. B. 1; 2. C. 2;1. D. – 2;1.
Lời giải:
Ta có : z = (1 - 6i) - (2 - 4i) = -1 -2i
Vậy chọn đáp án A.
III. Bài tập vận dụng
Câu 1: Cho số phức z = (2 + i)(1 - i) + 1 + 3i. Tính môđun của z.
A. 4√2. B. √13. C. 2√2. D. 2√5.
Lời giải:
Ta có: z = (2 + i)(1 - i) + 1 + 3i = (2.1 + 1.1) + (-1.2 + 1.1)i + 1 + 3i = 4 + 2i
. Vậy chọn đáp án D.
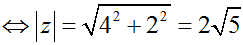
Câu 2: Số phức nghịch đảo của có phần ảo là:
A. 1 B. 1/2 C. -1 D. -1/2
Lời giải:
Chọn D.
Ta có: 
Câu 3: Phần thực của số phức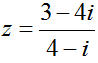 
bằng
A. 16/17 B. 3/4 C. -13/17 D. -3/4
Lời giải:
Chọn A.
Ta có: 
Câu 4: Số phức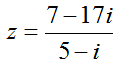 
có phần thực là
A. 3 B. 9/13 C. 2 D. -3
Lời giải:
Chọn C.
Ta có: 
⇒ Phần thực của z là: 2
Câu 5: Cho số phức z thỏa mãn điều kiện |z - 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích:
A. S = 9π B. S = 12π. C. S = 16π. D.S = 25π.
Lời giải:
Ta có:
<=> |w - 1 + i - 6 + 8i| ≤ 4 <=> |w - 7 + 9i| ≤ 4 (1)
Giả sử w = x + yi, khi đó (1) <=> (x - 7)2 + (y + 9)2 ≤ 16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4
Vậy diện tích cần tìm là S = π.42 = 16π
Chọn C.
Câu 6: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức
A.5 B.4 C.6 D.8
Lời giải:
Ta có:
Khi z = i thì A = 6
Chọn C.
Câu 7. Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất max M và giá trị nhỏ nhất min M của biểu thức M = |z2 + z + 1| + |z3 + 1|
A. max M = 5; min M = 1 B. max M = 5; min M = 2
C. max M = 4; min M = 1 D.max M = 4; min M = 2
Lời giải:
Ta có: M ≤ |z|2 + |z| + 1 + |z|3 + 1 = 5 ,
khi z = 1 thì M = 5 nên max M = 5
Mặt khác:
khi z = -1 thì M = 1 nên min M = 1
Chọn A.
Câu 8. Cho số phức z thỏa |z| ≥ 2 . Tìm tích của giá trị lớn nhất và nhỏ nhất của biểu thức:
Lời giải:
Ta có:
Mặt khác:
Vậy, giá trị nhỏ nhất của P là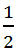 
, xảy ra khi z = -2i
giá trị lớn nhất của P bằng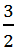 
xảy ra khi z = 2i
Chọn A.
Câu 9. Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức P = |1 + z| + 3|1 - z|
Lời giải:
Gọi z = x + yi.
Ta có:
=> y2 = 1 - x2 => x ∈ [-1; 1]
Ta có:
P = |1 + z| + 3|1 - z|
Xét hàm số:
Hàm số liên tục trên [-1; 1] và với x ∈ (-1; 1) ta có:
Ta có:
f(1) = 2; f(-1) = 6;
Chọn D.
Câu 10 . Cho số phức z thỏa mãn điều kiện |z2 + 4| = 2|z|. Khẳng định nào sau đây là đúng?
Lời giải:
Áp dụng bất đẳng thức |u| + |v| ≥ | u + v|, ta được:
2|z| + |-4| = |z2 + 4| + |-4| ≥ |z|2 => |z|2 - 2|z| - 4 ≤ 0 => |z| ≤ √5 + 1.
2|z| + |z|2 = |z2 + 4| + |-z2| ≥ 4 => |z|2 + 2|z| - 4 ≥ 0 => |z| ≥ √5 - 1
Vậy |z| nhỏ nhất là √5 - 1 khi z = -1 + i√5 và |z| lớn nhất là √5 + 1 khi z = 1 + i√5
Chọn B.
Câu 11. Cho z1; z2 là hai số phức liên hợp của nhau và thỏa mãn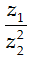 
∈ R và |z1 - z2| = 2√3. Tính môđun của số phức z1.
A. |z1| = √5
B. |z1| = 3
C. |z1| = 2
D. |z1| = 
Lời giải:
Gọi z1 = a + bi; z2 = a - bi.
Không mất tính tổng quát ta coi b ≥ 0
Do |z1 - z2| = 2√3 => |2bi| = 2√3 => b = √3
Do z1; z2 là hai số phức liên hợp của nhau nên z1; z2 ∈ R, mà:
Ta có:
(z1)3 = (a + bi)3 = (a3 - 3ab2) + (3a2b - b3)i ∈ R
Chọn C.
Xem thêm các dạng câu hỏi và bài tập liên quan khác:
60 Bài tập về phép chia số phức (có đáp án năm 2023)
60 Bài tập về số phức (có đáp án năm 2024)
60 Bài tập về ứng dụng hình học của tích phân (có đáp án năm 2024)
60 Bài tập về Hàm số lũy thừa (có đáp án năm 2024)
60 Bài tập về Khảo sát sự biến thiên và vẽ đồ thị hàm số (có đáp án năm 2024)
