Bài tập biểu diễn hình học các đại lượng của số phức
I. Lý thuyết
1. Định nghĩa
Số phức z = a + bi (a, b ) được biểu diễn bởi M(a; b) trong mặt phẳng toạ độ Oxy hay còn gọi là mặt phẳng phức. Và ngược lại mỗi điểm M(a; b) sẽ biểu diễn số phức z = a + bi.
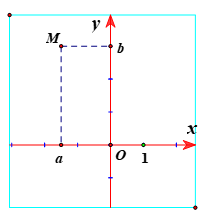
Trục Ox biểu diễn các số thực gọi là trục thực, trục Oy biểu diễn các số ảo gọi là trục ảo
Số phức z = a + bi (a, b ) cũng được biểu diễn bởi vectơ u→=(a;b), do đó M(a; b) là điểm biểu diễn của số phức z = a + bi (a, b ∈R) cũng có nghĩa là OM−→− biểu diễn số phức đó.
2. Tìm điểm biểu diễn hình học của số phức
Để tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện nào đó ta gọi M(x;y) biểu diễn số phức z rồi dựa vào điều kiện đã cho để tìm một hệ thức liên hệ giữa x;y mà kết luận tập hợp điểm. Nếu
a) ax + by + c = 0 thì tập hợp điểm là đường thẳng
b) (x-a)2 + (y-b)2 = r2thì tập hợp điểm là đường tròn tâm I(a;b) bán kính r.
Dựa vào biểu diễn hình học của số phức: Điểm M(a;b) biểu diễn cho số phức z=a+bi. Và ngược lại mỗi điểm M(a; b) sẽ biểu diễn số phức z = a + bi.
3. Tìm điểm biểu diễn của số phức z thỏa mãn điều kiện cho trước
Ta có: Nếu u→,v→ theo thứ tự biểu diễn các số phức z, z’ thì
u→+v→ biểu diễn số phức z + z’,
u→−v→ biểu diễn số phức z – z’,
ku→ (k∈R) biểu diễn số phức kz,
∣∣∣OM−→−∣∣∣=∣∣u→∣∣=|z|, với M là điểm biểu diễn của z.
II. Ví dụ minh họa
Ví dụ 1: Cho số phức z = 1+ 3i và số phức z’ = 2 + i. Hãy:
a) Biểu diễn số phức z và z’ trên mặt phẳng phức.
b) Biểu diễn số phức z + z’ và z’ – z trên mặt phẳng phức.
Lời giải
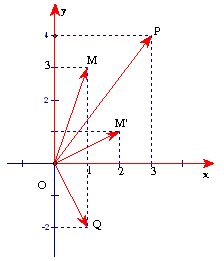
a) Biểu diễn số phức z = 1 + 3i là điểm M(1;3)
Biểu diễn số phức z’ = 2 + i là điểm M’(2;1)
b) z + z’ = 3 + 4i, biểu diễn trên mp phức bởi P(3;4
z’ – z = 1 – 2i, biểu diễn trên mp phức bởi Q(1;-2).
Ví dụ 2: Tập hợp số phức z trên hệ tọa độ phức mà thỏa mãn |z−3i|+|iz¯+3|=10.
Gọi z=x+yi.
Theo bài ra, ta có x2+(y−3)2−−−−−−−−−−−√+(y+3)2+x2−−−−−−−−−−−√=10.
⇒x2+(y−3)2=100+(y+3)2+x2−20(y+3)2+x2−−−−−−−−−−−√.
⇒10(y+3)2+x2−−−−−−−−−−−√=50+6y.
⇒25x2+16y2=400.
III. Bài tập vận dụng
Bài 1: Tập hợp số phức z trên hệ tọa độ phức mà thỏa mãn |z+1−i|=|z−1+2i|
Giả sử z=a+bi (a,b∈R). Ta có:
|z+1–i|=|z–1+2i|⇔|(a+1)+(b–1)i|=|(a–1)+(b+2)i| ⇔(a+1)2+(b–1)2=(a–1)2+(b+2)2 ⇔4a–6b–3=0
Vậy phương trình đường thẳng cần tìm là 4x–6y–3=0.
Bài 2: Tập hợp số phức z trên hệ tọa độ phức mà thỏa mãn |z+3i−2|=10
Mỗi số phức z=x+yi được biểu diễn bởi một điểm (x;y). Do đó, ta có tập số phức z thỏa mãn là:
|x+3i+yi−2|=10⇒(x−2)2+(y+3)2=100 là đường tròn tâm I(2,-3) và bán kính R=10.
Bài 3: Tìm tập hợp các điểm biểu diễn của số phức z sao cho u=z+2+3iz−i là một số thuần ảo.
Giải:
Đặt z=x+yi (x, y ∈ ℝ), khi đó:
u=(x+2)+(y+3)ix+(y−1)i=[(x+2)+(y+3)i][x−(y−1)i]x2+(y−1)2=(x2+y2+2x+2y−3)+2(2x−y+1)ix2+(y−1)2
u là số thuần ảo khi và chỉ khi:

Vậy tập hợp các điểm biểu diễn của z là đường tròn tâm I(-1,-1), bán kính 5–√, trừ điểm (0,1).
Bài 4: Trong mặt phẳng Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z−i|=|(1+i)z|
Giải:
Đặt z=x+yi (x,y ∈ ℝ)
Ta có:
|z−i|=|(1+i)z|⇔|x+(y−1)i|=|(x−y)+(x+y)i|⇔x2+(y−1)2=(x−y)2+(x+y)2
⇔x2+y2+2xy−1=0⇔x2+(y+1)2=2
Vậy tập hợp các điểm M biểu diễn các số phức z là đường tròn có phương trình x2+(y+1)2=2.
Bài 5: (Vận dụng) Trong các số phức z thỏa mãn điều kiện |z−2−4i|=|z−2i|. Tìm số phức z có module nhỏ nhất.
Giả sử số phức z cần tìm có dạng z = x + yi (x,y ∈ ℝ) và được biểu diễn bởi điểm M(x;y).
Ta có |x−2+(y−4)i|=|x+(y−2)i| (1) ⇔(x−2)2+(y−4)2−−−−−−−−−−−−−−−√=x2+(y−2)2−−−−−−−−−−−√
⇔y=−x+4. Do đó, tập hợp các điểm M biểu diễn các số phức z thỏa mãn (1) là đường thẳng x + y = 4.
Mặt khác, |z|=x2+y2−−−−−−√=x2+x2−8x+16−−−−−−−−−−−−−−√=2x2−8x+16−−−−−−−−−−−√
Ta có |z|=2(x−2)2+8−−−−−−−−−−−√≥22–√
Vậy |z|min⇔x=2⇒y=2. Do đó, z=2+2i.
Bài 6: (Vận dụng) Biết rằng số phức z thỏa mãn u=(z+3−i)(z¯¯¯+1+3i) là một số thực. Tìm giá trị nhỏ nhất của |z|.
Giải:
Đặt z=x+yi (x, y ∈ ℝ), ta có:
u=[(x+3)+(y−1)i][(x+1)−(y−3)i]=x2+y2+4x−4y+6+2(x–y−4)i
Ta có: u∈R⇔x−y−4=0
Tập hợp các điểm biểu diễn của z là đường thẳng d:x−y−4=0, M(x;y) là điểm biểu diễn của z. Môđun của z nhỏ nhất khi và chỉ khi độ dài OM nhỏ nhất ⇔OM⊥d. Tìm được M(-2;2) suy ra z=−2+2i.
Bài 7: (Vận dụng) Tìm số phức Z có mô đun lớn nhất và thỏa mãn điều kiện |z¯¯¯(1+i)−3+2i|=13√2.
Giải:
Gọi z=x+yi(x,y∈R) $\Rightarrow$ z¯=x−yi.
|z¯(1+i)−3+2i|=13√2⇔x2+y2−x−5y+398=0.
Gọi M (x;y) là điểm biểu diễn của z trong mặt phẳng tọa độ Oxy. Ta có M∈(C) là đường tròn có tâm I(12;52) và bán kính R=26√4.
Gọi d là đường thẳng đi qua O và I $\Rightarrow$ d: y=5x.
Gọi M1, M2 là hai giao điểm của d và (C). Ta có M1(34;154) và M2(14;54).
Ta thấy:
{OM1>OM2OM1=OI+R≥OM(M∈(C))
Vậy số phức cần tìm ứng với điểm biểu diễn M1 hay z=34+154i.
Bài 8: Cho số phức z=1–2i. Điểm nào dưới đây là điểm biểu diễn của số phức z trên mặt phẳng tọa độ?
A. Q(1;2)
B. N(2;1)
C. M(1;−2)
D. P(−2;1)
Bài 9: . Điểm biểu diễn hình học của số phức z=a+ai nằm trên đường thẳng:
A. y=x
B. y=2x
C. y=−x
D. y=−2x
Câu 10. Gọi A là điểm biểu diễn của số phức 5+8i và B là điểm biểu diễn của số phức −5+8i. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O.
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y=x.
Câu 11. Gọi A là điểm biểu diễn của số phức z=2+5i và B là điểm biểu diễn của số phức z′=−2+5i. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O.
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y=x.
Xem thêm các dạng câu hỏi và bài tập liên quan khác:
30 Bài tập về số phức (2024) có đáp án
60 Bài tập về phép chia số phức (có đáp án năm 2023)
60 Bài tập về số phức (có đáp án năm 2024)
60 Bài tập về Cực trị của hàm số (có đáp án năm 2024)
60 Bài tập về Khảo sát sự biến thiên và vẽ đồ thị hàm số (có đáp án năm 2024)




