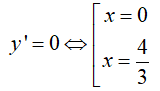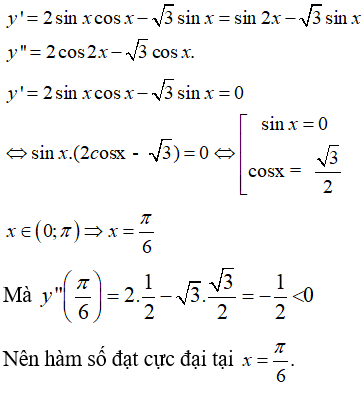60 Bài tập về Cực trị của hàm số (có đáp án năm 2024)

Kiến thức cần nhớ

1. Định nghĩa

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) và điểm $x_0\in (a;b)$ .

- Nếu tồn tại số h > 0 sao cho f (x) < f (x₀)  với mọi $x\in (x_0-h;x_0+h)$ và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực đại tại x₀ .

- Nếu tồn tại số h > 0 sao cho f (x) > f (x₀) với mọi $x\in (x_0-h;x_0+h)$ và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực tiểu tại x₀ .

2. Điều kiện cần để hàm số có cực trị

Định lý 1: Giả sử hàm số f(x) đạt cực trị tại điểm x_o. Khi đó, nếu f(x) có đạo hàm tại điểm x_o thì f‘(x_o) = 0.

Lưu ý:

- Đạo hàm f‘(x) có thể bằng 0 tại điểm x_o nhưng hàm số f(x) không đạt cực trị tại điểm x_o.

- Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.

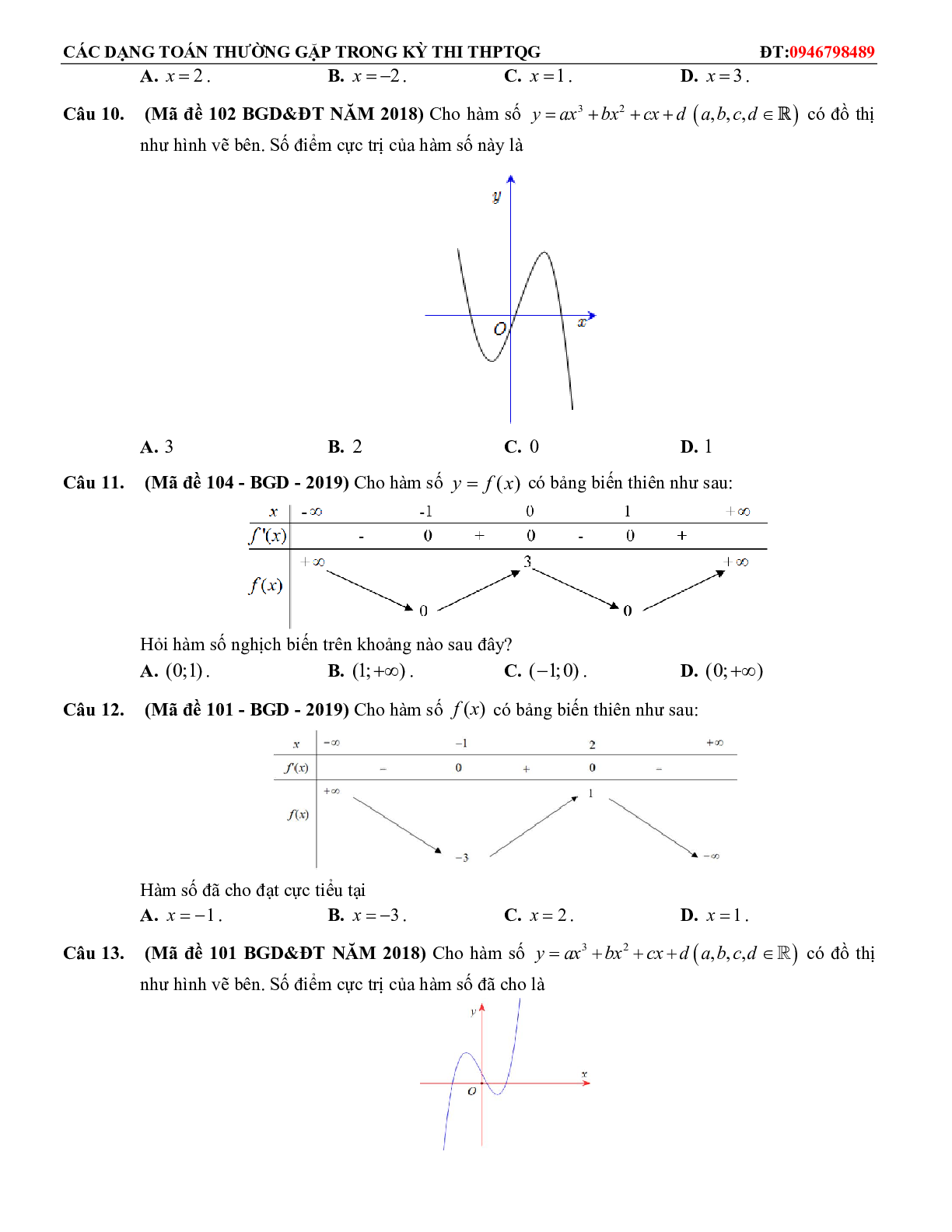
- Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng 0, hoặc tại đó hàm số không có đạo hàm.

- Hàm số đạt cực trị tại x_o và nếu đồ thị hàm số có tiếp tuyến tại điểm (x_o ; f(x_o)) thì tiếp tuyến đó song song với trục hoành.

Ví dụ : Hàm số y = |x| và hàm số y = x³

3. Điều kiện đủ để hàm số có cực trị

Định lý 2: Giả sử hàm số y = f(x) liên tục trên K = ( x₀ -h: x₀ +h ) và có đạo hàm trên K hoặc trên$K\backslash \text{{}{x}_0\text{}}$ , với h >0 .

- Nếu f '(x) > 0 trên khoảng (x₀ - h; x₀) và  trên $(x_0;x_0+h)$ thì x₀ là một điểm cực đại của hàm số f(x) .

- Nếu f '(x) < 0  trên khoảng (x₀ - h; x₀) và f '(x) > 0 trên $(x_0;x_0+h)$ thì x₀ là một điểm cực tiểu của hàm số f(x) .

Minh họa bằng bảng biến thiến

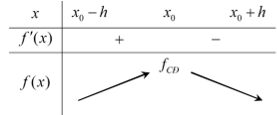
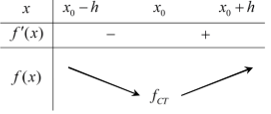
Lưu ý:

- Như vậy: Điểm cực trị phải là một điểm trong của tập hợp D (D ⊂ ℝ). Nếu f’(x) không đổi dấu thì hàm số không có cực trị.

(Nhấn mạnh: x_o ∈ (a; b)⊂ D nghĩa là x_o là một điểm nằm ở giữa trong của D).

Ví dụ: Hàm số  xác định trên D= [0,+∞). Ta có y ≥ y (0) với mọi x, nhưng x = 0 không phải là cực tiểu của hàm số vì D không chứa bất kì 1 lân cận nào của điểm 0.

^- Nếu hàm số y = f (x) đạt cực đại (cực tiểu) tại x₀ thì x₀ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f (x₀) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là f _CĐ ( f_CT ), còn điểm M (x₀;f( x₀)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

^- Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

- Giá trị cực đại (cực tiểu) f(x_o) nói chung không phải là GTLN (GTNN) của  f(x) trên tập hợp D.

- Hàm số có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập hợp D. Hàm số cũng có thể không có điểm cực trị.

- x_o là một điểm cực trị của hàm số f(x) thì điểm (x_o ; f(x_o)) được gọi là điểm cực trị của đồ thị hàm số f(x) .

4. Định lý 3: Giả sử hàm số f  có đạo hàm cấp một trên khoảng (a; b) chứa điểm x_o ;  f ‘(x_o) = 0 và f  có đạo hàm cấp hai khác 0 tại điểm x_o

a) Nếu f ”(x_o) < 0 thì hàm số f  đạt cực đại tại điểm x_o
b) Nếu f ”(x_o) < 0 thì hàm số f  đạt cực tiểu tại điểm x_o

Lưu ý:

- Không cần xét hàm số f(x) có hay không có đạo hàm tại điểm x = x_o nhưng không thể bỏ qua điều kiện hàm số liên tục tại điểm x_o.

Các dạng bài tập về cực trị của hàm số

Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số đó

Dạng 2. Tìm cực trị của hàm số khi biết y, y’

Dạng 3. Tìm m để hàm số đạt cực trị tại x = x0

Dạng 4. Tìm m để hàm số có n cực trị

Dạng 5. Đường thẳng đi qua 2 điểm cực trị

Dạng 6. Tìm m để hàm số có cực trị thỏa mãn điều kiện cho trước

Dạng 7. Tam giác cực trị 

Dạng 8. Bài toán cực trị hàm số chứa dấu trị tuyệt đối

Dạng 9. Tìm cực trị của hàm số f(u) khi biết bảng biến thiên, đồ thị f’(x)

Bài tập tự luyện

1 Bài tập vận dụng

Bài 1. Áp dụng quy tắc I, hãy tìm các điểm cực trị của các hàm số sau:

a) y = x⁴ – 2x³ + x² – 8;

b) $y=\frac{x-3}{x+4}$

Lời giải:

a) TXĐ: D = $\mathrm{ℝ}$.

Ta có: y’ = 4x³ – 6x² + 2x

$y\text{'}=0$$\iff \left[\begin{array}{c}x=1\\ x=\frac{1}{2}\\ x=0\end{array}\right.$

Bảng biến thiên:

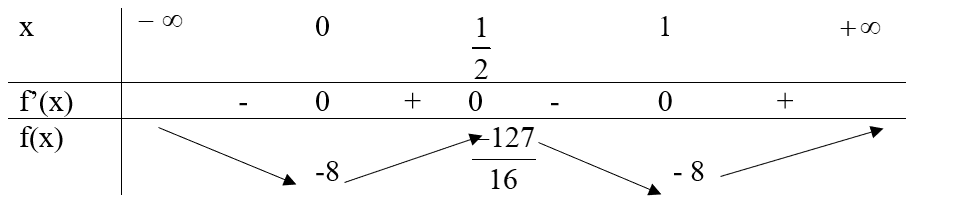
Hàm số đạt cực tiểu tại x = 0 và x = 1; f_CT = f(0) = f(1) = – 8

Hàm số đạt cực đại tại $x=\frac{1}{2};$$\hspace{0.17em}{f}_{CD}=\frac{-127}{16}$

b) $y=\frac{x-3}{x+4}$

TXĐ: D = R\{– 4}.

$y\text{'}=\frac{7}{{(x\text{\hspace{0.17em}}+4)}^2}>0$$\forall x\ne -4$

Phương trình y’ = 0 vô nghiệm nên hàm số không có cực trị.

Bài 2. Tìm cực trị của hàm số $f\left(x\right)=x^4-2x^2+\text{\hspace{0.17em}\hspace{0.17em}}10$.

Lời giải:

Hàm số đã cho xác định với mọi x

Ta có: f’(x) = 4x³ – 4x

$f\text{'}\left(x\right)=0$$\hspace{0.17em}\iff \left[\begin{array}{c}x=0\\ x=\pm 1\end{array}\right.$

Ta có: f”(x) = 12x² – 4

Suy ra: f”(0) = – 4 < 0 nên x = 0 là điểm cực đại.

f”(1) = f”(– 1)  = 8 > 0 nên x = 1 và x = –1 là điểm cực tiểu.

Kết luận:

Hàm số f(x) đạt cực tiểu tại x = 1 và x = – 1; f_CT = f(1) = f(–1) = 9.

Hàm số f(x) đạt cực đại tại x = 0 và f_CD = f(0) = 10.

Bài 3. Áp dụng quy tắc II, hãy tìm các điểm cực trị của các hàm số sau:

a) y = 2x⁴ – 4x²  + 2;

b) y = x⁵ – 2x³ + x + 1;

c) $y=x^2+\frac{2}{x}$

Lời giải:

a) y = 2x⁴ – 4x²  + 2

TXĐ: D = R.

Ta có: y’ = 8x³ – 8x.

$y\text{'}=0$$\hspace{0.17em}\iff \left[\begin{array}{c}x=0\\ x=\pm 1\end{array}\right.$

Đạo hàm cấp hai: y” (x) = 24x² – 8

Vì y”(– 1) = 16 > 0; y”(1) = 16 > 0 nên hàm số đạt cực tiểu tại x = – 1; x = 1 và y_CT = y(1) = y(– 1) = 0.

và y” (0) = –8 < 0 nên hàm số đạt cực đại tại x = 0 và y_CD = y(0) = 2.

b) y = x⁵ – 2x³ + x + 1

TXĐ: D = R.

Ta có: y’ = 5x⁴ – 6x² + 1

$y\text{'}=0$$\hspace{0.17em}\iff \left[\begin{array}{c}x=\pm 1\\ x=\pm \frac{1}{\sqrt{5}}\end{array}\right.$

Đạo hàm cấp hai: y” = 20x³ – 12x

Và y”(1)  = 8 > 0 nên hàm số đạt cực tiểu tại x = 1.

y”(– 1) = – 8 < 0 nên hàm số đạt cực đại tại x = – 1.

$y"\left(\frac{1}{\sqrt{5}}\right)\text{}$$\hspace{0.17em}\hspace{0.17em}=\text{\hspace{0.17em}\hspace{0.17em}}\frac{-8\sqrt{5}}{5}\text{\hspace{0.17em}\hspace{0.17em}}<0$ nên hàm số đạt cực đại tại $x=\frac{1}{\sqrt{5}}$

$y"\left(\frac{-1}{\sqrt{5}}\right)\text{}$$\hspace{0.17em}\hspace{0.17em}=\text{\hspace{0.17em}\hspace{0.17em}}\frac{8\sqrt{5}}{5}\text{\hspace{0.17em}\hspace{0.17em}}>0$ nên hàm số đạt cực tiểu tại $x=-\frac{1}{\sqrt{5}}$

Vậy hàm số đã cho có 2 điểm cực đại, 2 điểm cực tiểu.

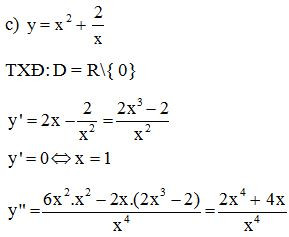
y”(1) = 6 > 0 nên hàm số đạt cực tiểu tại x = 1 và y_CT = y(1) = 3.

Bài 4. Tìm tất cả các giá trị của tham số m để hàm số  y = x³ – mx²  + (2m – 3).x – 3 đạt cực đại tại  x = 1.

Lời giải:

TXĐ: D = R.

Và y’ = 3x² – 2mx + 2m – 3;

 y” (x) = 6x – 2m

Để hàm số đã cho đạt cực đại tại x = 1 thì:

$$\begin{gathered} \left\{\begin{array}{c}y\text{'}\left(1\right)=0\\ y"\left(1\right)<0\end{array}\right. \\ \iff \left\{\begin{array}{c}3-2m+2m-3=0\\ 6-2m<0\end{array}\right. \\ \hspace{0.17em}\iff \left\{\begin{array}{c}0=0\left(ld\right)\\ m>3\end{array}\right.\iff m>\text{\hspace{0.17em}}3 \end{gathered}$$

Vậy để hàm số đã cho đạt cực đại tại x = 1 thì m > 3.

Bài 5. Tìm tất cả các giá trị của tham số m để hàm số y = x³ - 2x² +mx + 1 đạt cực đại tại x = 1.

Lời giải:

Bài 6 Cho hàm số y = x³ - 2x² + 3. Điểm M(0; 3) là?

Lời giải:

Bài 7. Tìm điểm cực đại của hàm số y = sin2x + $\sqrt{3}$cosx + 1 với x ∈ (0; π)

Lời giải:

Bài 8. Có bao nhiêu mệnh đề đúng trong các phát biểu sau?

1. Hàm số không có đạo hàm tại x = 0.

2. Hàm số không liên tục tại x = 0.

3. Hàm số không có cực trị tại x = 0.

4. Hàm số đạt cực trị tại x = 0.

Lời giải:

Hiển thị đáp án

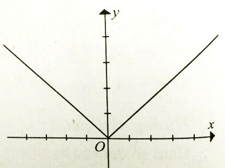
Đồ thị hàm số y = |x| có dạng hình vẽ.

Từ đồ thị trong hình ta có hàm số y = |x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó. Sử dụng định nghĩa cực trị ta có hàm số y = |x| đạt cực tiểu tại x = 0

Do đó mệnh đề 1 và 4 đúng.

Bài 9. Cho hàm số y = -3x⁴ - 2x³ + 3. Hàm số có?

Lời giải:

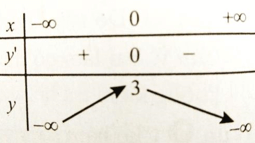
Ta có y' = -12x³ - 4x

Xét y'=0 => x = 0

Hàm số chỉ có một cực đại tại x = 0.

Bài 10. Cho hàm số y = x⁴ - 2(m - 1)x² + m². Tìm m để hàm số có 3 điểm cực trị là 3 đỉnh của 1 tam giác vuông

Lời giải:

2 Bài tập tự luyện có hướng dẫn

Xem thêm các dạng bài tập liên quan khác:

60 Bài tập về Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có đáp án năm 2023)

60 Bài tập về sự đồng biến, nghịch biến của hàm số (có đáp án năm 2023)

60 Bài tập về Hàm số lũy thừa (có đáp án năm 2023)

60 Bài tập về Lôgarit (có đáp án năm 2023)

60 Bài tập về Phương trình mũ và phương trình logarit (có đáp án năm 2024)