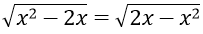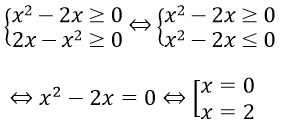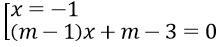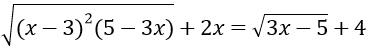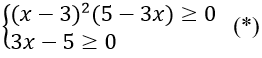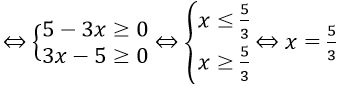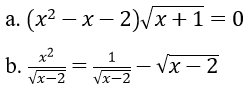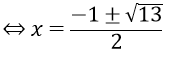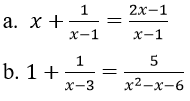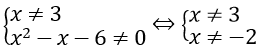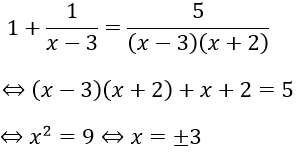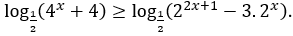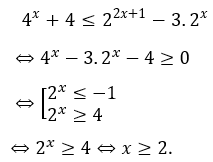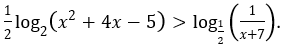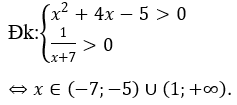30 bài tập biến đổi phương trình và bất phương trình cùng cơ số 2024 (có đáp án)

Bài tập biến đổi phương trình và bất phương trình cùng cơ số

I. Lý thuyết

A. Phương trình

- Phương trình tương đương: Hai phương trình f₁(x) = g₁(x) và f₂(x) = g₂(x) được gọi là tương đương nếu chúng có cùng tập nghiệm

- Kí hiệu là f₁(x) = g₁(x) ⇔ f₂(x) = g₂(x)

- Phép biến đổi không làm thay đổi tập nghiệm của phương trình gọi là phép biến đổi tương đương.

- Phương trình hệ quả: f₂(x) = g₂(x) gọi là phương trình hệ quả của phương trình f₁(x) = g₁(x) nếu tập nghiệm của nó chứa tập nghiệm của phương trình f₁(x) = g₁(x)

- Kí hiệu là f₁(x) = g₁(x) ⇒ f₂(x) = g₂(x)

- Để giải phương trình ta thực hiện các phép biến đổi để đưa về phương trình tương đương với phương trình đã cho đơn giản hơn trong việc giải nó. Một số phép biến đổi thường sử dụng:

   + Cộng (trừ) cả hai vế của phương trình mà không làm thay đổi điều kiện xác định của phương trình ta thu được phương trình tương đương phương trình đã cho.

   + Nhân (chia) vào hai vế với một biểu thức khác không và không làm thay đổi điều kiện xác định của phương trình ta thu được phương trình tương đương với phương trình đã cho.

   + Bình phương hai vế của phương trình ta thu được phương trình hệ quả của phương trình đã cho.

Bình phương hai vế của phương trình (hai vế luôn cùng dấu) ta thu được phương trình tương đương với phương trình đã cho.

B. Bất phương trình

1. Định nghĩa

Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.

2. Phương trình lôgarit cơ bản

 = b ⇔ x = ab (0 < a ≠ 1).

 <=> 

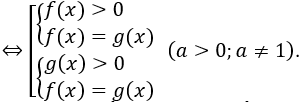
3. Các bước giải phương trình logarit bằng cách đưa về cùng cơ số

* Bước 1. Tìm điều kiện của phương trình (nếu có).

* Bước 2. Sử dụng định nghĩa và các tính chất của lôgarit để đưa các lôgarit có mặt trong phương trình về cùng cơ số.

* Bước 3.Biến đổi phương trình về phương trình lôgarit cơ bản đã biết cách giải.

* Bước 4. Kiểm tra điều kiện và kết luận.

II. Ví dụ minh họa

Ví dụ 1: Giải phương trình

Lời giải:

Điều kiện:

Thử lại ta thấy cả x = 0 và x = 2 đều thỏa mãn phương trình

Vậy tập nghiệm của phương trình là S = {0;2}

Ví dụ 2: Giải phương trình:

Với điều kiện trên phương trình đã cho tương đương với phương trình

<=>  + 2x - 8 = 0

Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là {2}.

III. Bài tập vận dụng

Bài 1: Giải phương trình

Lời giải chi tiết:

Điều kiện: x > 0

Phương trình đã cho tương đương với phương trình:

<=>  = 0 <=>  = 0 <=> x = 1

Vật phương trình đã cho có nghiệm x = 1

Bài 2: Tìm tập nghiệm S của phương trình log₃(2x+1) -log₃(x-1) = 1

Lời giải chi tiết:

Ta có điều kiện xác định 0 2x + 1> 0 và x - 1 >  <=> x > 1

 = 1

<=>  = 1

<=> 

<=> 

<=> 

<=> x = 4 ( thỏa mãn điều kiện xác định)

Bài 3: Gọi x1, x2 là nghiệm của phương trình  . Tính x1, x2

Lời giải chi tiết:

Điều kiện: x > 0 và x khác 1

<=> 

<=> 

<=> 

<=>  x = 4 hoặc x = 1/4 (thỏa mãn điều kiện đưa ra)

Vậy tích x1. x1 = 4. 1/4 = 1

Bài 4: Tổng tất cả các nghiệm thực của phương trình

Lời giải chi tiết:

Điều kiện xác định: x > 0

Khi đó  <=>  <=> 

<=>  hoặc  <=>   hoặc 

Do đó tổng tất cả các nghiệm của phương trình đã cho bằng 

Bài 5: Tìm m để cặp phương trình sau tương đương

x² + mx - 1 = 0  (1) và (m-1)x² + 2(m-2)x + m - 3 = 0   (2)

Lời giải:

Giả sử hai phương trình (1) và (2) tương đương

Ta có (m-1)x² + 2(m-2)x + m - 3 = 0

⇔ 

Do hai phương trình tương đương nên x = -1 cũng là nghiệm của phương trình  (1)

Thay x = -1 vào phương trình (1) ta được m = 0

Với m = 0 thay vào hai phương trình ta thấy không tương đương.

Vậy không có giá trị nào của m thỏa mãn.

Bài 6: Giải phương trình

Lời giải:

Điều kiện:

Ta thấy x = 3 thỏa mãn điều kiện (*)

Nếu x ≠ 3. thì (*)

Do đó điều kiện xác định của phương trình là x = 3 hoặc x = 5/3

Thay x = 3 và x = 5/3 vào phương trình thấy chỉ có x = 3 thỏa mãn

Vậy phương trình đã cho có nghiệm duy nhất S = {3}

Bài 7: Giải phương trình

Lời giải:

a. Điều kiện: x ≥ -1.

Ta có x = -1 là một nghiệm.

Nếu x > -1 thì √(x+1) > 0. Do đó phương trình tương đương

x² - x - 2 = 0 ⇔ x = -1 hoặc x = 2.

Đối chiếu điều kiện ta được nghiệm của phương trình là x = -1, x = 2.

Vậy phương trình đã cho có hai nghiệm S = {-1; 2}

b. ĐKXĐ: x > 2

Với điều kiện đó phương trình tương đương với phương trình

x² = 1 - (x - 2)⇔ x² + x - 3 = 0

Đối chiếu với điều kiện ta thấy không có giá trị nào thỏa mãn

Vậy phương trình vô nghiệm

Bài 8: Giải phương trình

Lời giải:

a. Điều kiện: x ≠ 1.

Với điều kiện trên phương trình tương đương x² - x + 1 = 2x - 1 ⇔ x = 1 hoặc x = 2

Đối chiếu điều kiện ta được phương trình có nghiệm duy nhất x = 2.

b. ĐKXĐ : 

Với điều kiện đó phương trình tương đương với

Đối chiếu với điều kiện ta có nghiệm của phương trình là x = -3

Bài 9: Giải bất phương trình sau

Lời giải:

Bất phương trình tương đương

Vậy tập nghiệm của bất phương trình là [2;+∞).

Bài 10: Giải bất phương trình sau

Lời giải:

Xem thêm các dạng câu hỏi và bài tập liên quan khác:

500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2024) 

100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2024)

200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2024) 

30 Bài tập bài tập tập hợp tất cả giá trị thoả mãn bất phương trinh tích thương 2024 (có đáp án) 

30 bài tập về bất phương trình (2024) có đáp án