Bài tập về tập hợp tất cả giá trị thoả mãn bất phương trinh tích thương

I. Phương pháp giải

1. Bất phương trình dạng tích:$A\left(x\right).B\left(x\right)>0$ ;

                             (hoặc $A\left(x\right).B\left(x\right)<0;A\left(x\right).B\left(x\right)\ge 0;A\left(x\right).B\left(x\right)\le 0$);

2. Bất phương trình dạng thương: $\frac{A\left(x\right)}{B\left(x\right)}>0$

                                      (hoặc $\frac{A\left(x\right)}{B\left(x\right)}<0;\frac{A\left(x\right)}{B\left(x\right)}\ge 0;\frac{A\left(x\right)}{B\left(x\right)}\le 0$).

3. Định lý về dấu của nhị thức bậc nhất $ax+b(a\ne 0)$:

Nhị thức bậc nhất cùng dấu với a khi $x>-\frac{b}{a}$

Nhị thức bậc nhất trái dấu với a khi $x<-\frac{b}{a}$

Do $-\frac{b}{a}$ là nghiệm của nhị thức $ax+b$ nên định lý được phát biểu:

Nhị thức $ax+b(a\ne 0)$ cùng dấu với a với các giá trị của x lớn hơn nghiệm của nhị thức, trái dấu với a với các giá trị của x nhỏ hơn nghiệm của nhị thức.

4. Phương pháp giải các bất phương trình dạng tích, thương: Phân tích thành nhân tử chứa các nhị thức bậc nhất. Lập bảng xét dấu của nhị thức bậc nhất $ax+b$

II. Một số ví dụ

Ví dụ 1: Giải bất phương trình $(2x-9)(1945+x)>0$.

Tìm cách giải: Với tích $A.B>0$ xảy ra khi A và B cùng dấu. Do đó $A>0$ và $B>0$ hoặc $A<0$ và $B<0$. Ta có cách giải:

Giải

Cách 1: Bất phương trình đã cho tương đương với:

$\begin{array}{l}\iff [\begin{array}{l}\{\begin{array}{l}2x-9>0\\ 1945+x>0\end{array}\\ \{\begin{array}{l}2x-9<0\\ 1945+x<0\end{array}\end{array}\iff [\begin{array}{l}\{\begin{array}{l}2x>9\\ x>-1945\end{array}\\ \{\begin{array}{l}2x<9\\ x<-1945\end{array}\end{array}\\ \iff [\begin{array}{l}\{\begin{array}{l}x>4,5\\ x>-1945\end{array}\\ \{\begin{array}{l}x<4,5\\ x<-1945\end{array}\end{array}\iff [\begin{array}{l}x>4,5\\ x<-1945\end{array}\end{array}$

Vậy nghiệm của bất phương trình là $x>4,5;x<-1945$.

* Chú ý: Bằng việc lập bảng xét dấu của từng thừa số của tích là nhị thức bậc nhất ta có cách 2: Lập bảng xét dấu:

Vậy nghiệm của bất phương trình: $x>4,5$ hoặc $x<-1945$.

Ví dụ 2: Giải bất phương trình $\left(x-6\right)\left(x+10\right)<-x^2+x+30$.

* Tìm cách giải: Ta phân tích vế phải thành nhân tử, xuất hiện nhân tử chung và chuyển vế để đưa về phương trình tích.

Giải

a)     Ta có:

 $\begin{array}{l}-x^2+x+30\\ =-x^2+6x-5x+30\\ =-\left(x-6\right)\left(x+5\right)\end{array}$

Do đó bất phương trình thành $\left(x-6\right)\left(x+10\right)+\left(x-6\right)\left(x+5\right)<0$

$\iff \left(x-6\right)\left(2x+15\right)<0$. Lập bảng xét dấu:

Nghiệm của bất phương trình là: $-7,5<x<6$.

III. Bài tập vận dụng

Câu 1: Giải bất phương trình $x^4+36\ge 13x^2$ sau đó biểu diễn nghiệm trên trục số.

* Tìm cách giải: Chuyển tất cả về một vế rồi phân tích vế đó thành nhân tử và giải bất phương trình tích.

Giải

Ta có $x^4+36\ge 13x^2\iff x^4-13x^2+36\ge 0$

$\begin{array}{l}\iff x^4-9x^2-4x^2+36\ge 0\\ \iff \left(x^2-9\right)\left(x^2-4\right)\ge 0\end{array}$

$\iff \left(x-2\right)\left(x+2\right)\left(x-3\right)\left(x+3\right)\ge 0$. Lập bảng xét dấu:

Nghiệm của bất phương trình là: $[\begin{array}{l}x\le -3\\ -2\le x\le 2\\ x\ge 3\end{array}$. Biểu diễn nghiệm:

Câu 2:  Giải bất phương trình: $\frac{2016-6x}{x\left(x+8\right)}\le 0$.

* Tìm cách giải: Đây là bất phương trình dạng thương của $\left(2016-6x\right)$ chia cho $x\left(x-8\right)$.

Ta có:

 $\begin{array}{l}2016-6x=0\iff x=336;\\ x+8=0\iff x=-8\end{array}$.

Giải

ĐKXĐ: $x\ne 0$ và $x\ne -8$. Đặt $A=\frac{2016-6x}{x\left(x+8\right)}$. Lập bảng xét dấu:

$A\le 0$ khi $[\begin{array}{l}-8<x<0\\ x\ge 336\end{array}$.

Câu 3: Giải bất phương trình $\frac{-x^2-5x+28}{x^2+2x-15}\ge -2\left(1\right)$

Và biểu diễn nghiệm trên trục số.

* Tìm cách giải: Nếu chuyển vế, rút gọn vế trái ta được bất phương trình dạng thương. Phân tích các tử, mẫu thành nhân tử rồi lập bảng xét dấu.

Giải

ĐKXĐ: $x\ne 3;x\ne -5$

$\begin{array}{l}\left(1\right)\iff \frac{-x^2-5x+28}{x^2+2x-15}+2\ge 0\\ \iff \frac{x^2-x-2}{x^2+2x-15}\ge 0\\ \iff \frac{\left(x+1\right)\left(x-2\right)}{\left(x-3\right)\left(x+5\right)}\ge 0\end{array}$

Lập bảng xét dấu ta có:

Nghiệm của bất phương trình là $[\begin{array}{l}x<-5\\ -1\le x\le 2\\ x>3\end{array}$. Biểu diễn nghiệm:

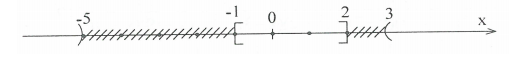
Câu 4: Cho biểu thức $A=\left[\frac{5}{x+3}-\frac{5x-15}{2x-9}.\left(\frac{2x-9}{x^2-9}-2x+9\right)\right]:\frac{1-x}{1+x}$.

Tìm x để $A<0$

* Tìm cách giải: Khi rút gọn biểu thức và khi tìm x để $A<0$ cần lưu ý ĐKXĐ. Do sau khi chia $1-x$ cũng thành mẫu số nên $x\ne \pm 1$.

Giải

Rút gọn A: ĐKXĐ: $x\ne \pm 3;x\ne \pm 1;x\ne 4,5$. Ta có:

$A=\left[\frac{5}{x+3}-\frac{5\left(x-3\right)}{\left(2x-9\right)}.\frac{\left(2x-9\right)\left(1-x^2+9\right)}{\left(x-3\right)\left(x+3\right)}\right].\frac{1+x}{1-x}$

    $\begin{array}{l}=\left[\frac{5}{x+3}-\frac{5\left(1-x^2+9\right)}{x+3}\right].\frac{1+x}{1-x}\\ =\frac{5\left(x-3\right)\left(x+3\right)}{x+3}.\frac{1+x}{1-x}\\ =\frac{5\left(x-3\right)\left(1+x\right)}{1-x}\end{array}$

Lập bảng xét dấu:

Vậy để $A<0$ thì $[\begin{array}{l}-1<x<1\\ x>3;x\ne 4,5\end{array}$.

Câu 5: Giải bất phương trình:

                   $\frac{1}{x^2-x}+\frac{1}{x^2-3x+2}+\frac{1}{x^2-5x+6}+...+\frac{1}{x^2-39x+380}<0$.

* Tìm cách giải: Bất phương trình có ẩn ở mẫu nên lưu ý ĐKXĐ.

Ta có $x^2-x=x\left(x-1\right);x^2-3x+2=\left(x-1\right)\left(x-2\right);...$ có dạng tổng quát $A.\left(A-1\right)$.

Mà $\frac{1}{A\left(A-1\right)}=\frac{A-\left(A-1\right)}{A\left(A-1\right)}=\frac{1}{A-1}-\frac{1}{A}$. Ta phân tích các phân thức ở vế trái rồi rút gọn, sẽ được một phân thức dạng thương.

Giải

ĐKXĐ: $x\notin \left\{0;1;2;3;....;19;20\right\}$.

Biến đổi bất đẳng thức thành:

$\frac{1}{x\left(x-1\right)}+\frac{1}{\left(x-1\right)\left(x-2\right)}+\frac{1}{\left(x-2\right)\left(x-3\right)}+...+\frac{1}{\left(x-19\right)\left(x-20\right)}<0$

$\iff \frac{1}{x-1}-\frac{1}{x}+\frac{1}{x-2}-\frac{1}{x-1}+...+\frac{1}{x-20}-\frac{1}{x-19}<0$

$\iff \frac{1}{x-20}-\frac{1}{x}<0\iff \frac{20}{x\left(x-20\right)}<0$.

Đặt $A=\frac{20}{x\left(x-20\right)}$. Lập bảng xét dấu

$A<0$ khi $x\notin \left\{1;2;3;...;19\right\}$và $0<x<20$.

Câu 6:  Giải bất phương trình $\frac{m-5}{x-2}>3$ với m là tham số.

* Tìm cách giải: Bất phương trình có ẩn ở mẫu là có tham số nên phải lưu ý ĐKXĐ và biện luận tham số m khi giải bất phương trình.

Giải

ĐKXĐ: $x\ne 2$

$\frac{m-5}{x-2}>3\iff \frac{m-5}{x-2}-3>0\iff \frac{\left(m+1\right)-3x}{x-2}>0$

Ta thấy $m+1-3x=0\iff x=\frac{m+1}{3}$.

Ta có $\frac{m+1}{3}>2\iff m>5$ và $\frac{m+1}{3}<2\iff m<5$.

Đặt $B=\frac{\left(m+1\right)-3x}{x-2}$.

Lập bảng xét dấu: khi $m>5$

Với $m>5$ ta có nghiệm của bất phương trình là: $2<x<\frac{m+1}{3}$.

Lập bảng xét dấu: khi $m<5$

Với $m<5$ ta có nghiệm của bất phương trình là: $\frac{m+1}{3}<x<2$

Câu 8: Lập bất phương trình cho bài toán sau:

Cô Mai chia đều 10 cái kẹo cho 2 bạn nhỏ. Hỏi mỗi bạn được bao nhiêu cái kẹo để sau khi chia xong cô Mai vẫn còn kẹo?

A. 2x < 10

B. 2x > 10

C. 10x < 2

D. 10x > 2

Trong đó, x là số kẹo mỗi bạn nhận được

Lời giải: Chọn đáp án A.

Gọi số kẹo mỗi bạn nhận được là x (cái kẹo)

Khi đó, 2 bạn sẽ có tất cả 2x (kẹo)

Để sau khi chia kẹo xong, cô Mai vẫn còn kẹo thì 2x < 10

Câu 9:  Bạn Oanh có 15000 đồng, Oanh muốn mua x quyền vở  và 1 cái bút giá 4000 đồng, biết giá mỗi quyền vở là 3000 đồng, Lập phương trình liên quan ẩn x?

A. 4000 + 3000.x < 15000

B. 4000 + 3000x > 15000

C. 3000x < 15000

D. Tấy cả đáp án đều sai

Lời giải: Chọn đáp án B

Giá của x quyển vở là 3000x (đồng)

Tổng số tiền mua 1 cái bút và x quyển vở là 4000 + 3000. X ( đồng)

Vì số tiền bạn Oanh có 15000 nên ta có bất phương trình sau: 4000 + 3000.x < 15000

Câu 10:: kết luận nào sau đây là đúng khi nói về nghiệm của bất phương trình (x + 4)(x+4) > (x-1)( x + 9) + 25

A. Bất phương trình vô nghiệm

B. Bất phương trình có vô số nghiệm 

C. Bất phương trình có tập nghiệm S = {x > 0}

D. Bất phương trình có tập nghiệm S = {x < 0}

Lời giải: Chọn đáp án B

Ta có (x + 4)(x + 4) > (x -2)(x +10) + 25

<=> x² + 8x + 16 > x² + 8x - 20 + 25

<=> x² + 8x + 16 - x² - 8x + 20 - 25 > 0

<=> 11 > 0 

Vì 11 > 0 luôn đúng nên phương trình có vô số ngiệm.

Xem thêm các dạng câu hỏi và bài tập liên quan khác:

300 Bài tập Toán 8 chương 4: Bất phương trình bậc nhất một ẩn (có đáp án năm 2024) 

500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2024) 

100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2024) - Toán 10 

30 bài tập về bất phương trình (2024) có đáp án 

30 Bài tập về miền nghiệm của bất phương trình (2024) có đáp án