Bài tập hệ bất phương trình bậc nhất hai ẩn
Kiến thức cần nhớ
1. Hệ bất phương trình bậc nhất hai ẩn
- Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn.
- Cặp số (x0;y0) là nghiệm của một hệ bất phương trình bậc nhất hai ẩn khi (x0;y0) đồng thời là nghiệm của tất cả các bất phương trình trong hệ đó.
Ví dụ:
{x+2y<9y−2x>9là một hệ bất phương trình hai ẩn gồm 2 bất phương trình x+2y<9 và y−2x>9.
{x2+y2<5x−y>4 không phải là hệ bất phương trình bậc nhất hai ẩn bởi x2+y2<5 là bất phương trình bậc
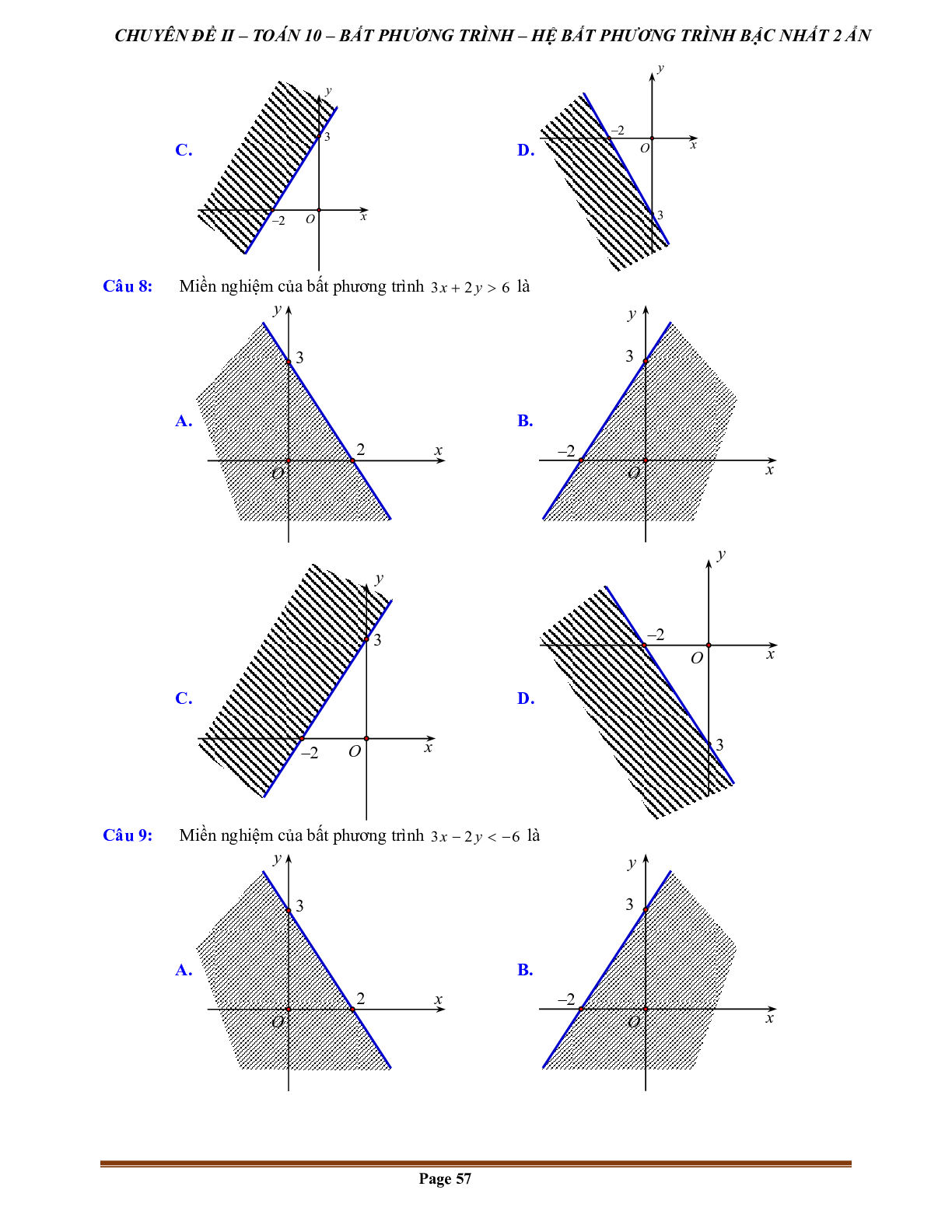
hai 2 ẩn.
- Cho hệ bất phương trình hai ẩn {x+y>9x−y<9.
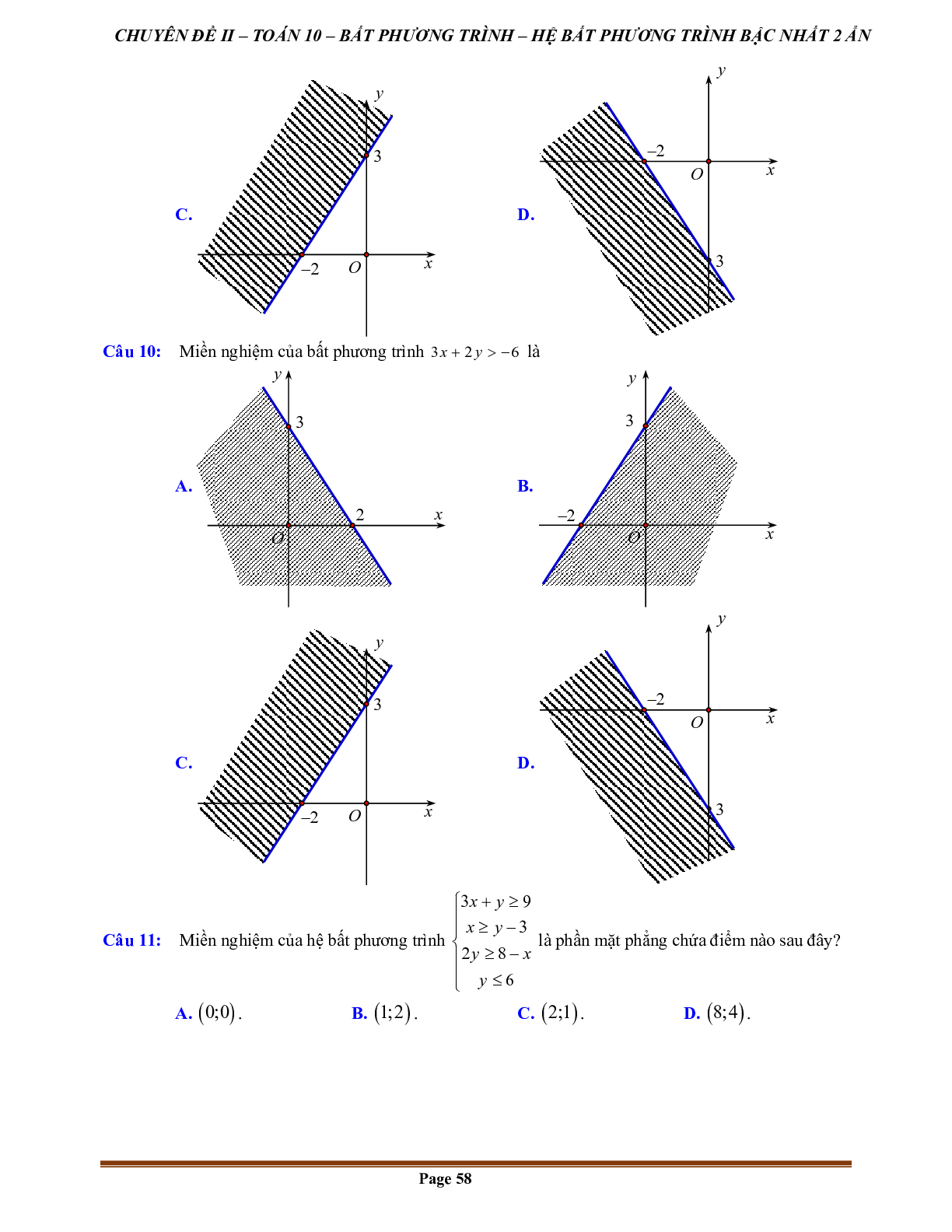
Cặp (x; y) = (10; 2) là nghiệm của bất phương trình x + y > 9 và cũng là nghiệm của bất phương trình x – y < 9. Nên cặp (x; y) = (10; 2) là nghiệm của hệ bất phương trình trên.
2. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
- Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn là miền nghiệm của hệ bất phương trình đó.
- Miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.
- Cách xác định miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn:
+ Trên cùng một mặt phẳng tọa độ, xác định miền nghiệm của mỗi bất phương trình bậc nhất hai ẩn trong hệ và gạch bỏ miền còn lại.
+ Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.
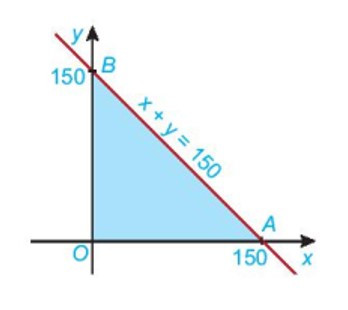
Ví dụ: Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn:{x≥0y≥0x+y≤150:
Bước 1: Xác định miền nghiệm D1 của bất phương trình x ≥ 0 và gạch bỏ phần miền còn lại.
- Đường thẳng x = 0 là trục tọa độ Oy.
- Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy nằm bên phải trục Oy.
Bước 2: Tương tự, miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox nằm bên trên trục Ox.
Bước 3: Miền nghiệm D3 của bất phương trình x + y ≤ 150:
- Vẽ đường thẳng d: x + y = 150.
- Vì 0 + 0 ≤ 150 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 150.
Do đó, miền nghiệm D3 của bất phương trình x + y ≤ 150 là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Từ đó ta có miền nghiệm tô màu xanh chính là giao miền nghiệm của các bất phương trình trong hệ.
3. Ứng dụng của hệ bất phương trình bậc nhất hai ẩn
Nhận xét: Tổng quát, người ta chứng minh được rằng giá trị lớn nhất (hay nhỏ nhất) của biểu thức F(x;y)=ax+by, với (x;y) là tọa độ các điểm thuộc miền đa giác A1A2...An, tức là các điểm nằm bên trong hay nằm trên các cạnh của đa giác, đạt được tại một trong các đỉnh của đa giác đó.
Ví dụ: Cho hệ bất phương trình bậc nhất hai ẩn: {x≥0y≥0x+y≤1002x+y≤120và F(x;y)=3,5x+2y. Tìm giá trị lớn nhất của F(x;y).
Hướng dẫn giải:
Bước 1: Xác định miền nghiệm của hệ bất phương trình trên.
- Xác định miền nghiệm D1 của bất phương trình x ≥ 0.
- Đường thẳng x = 0 là trục tọa độ Oy.
- Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy nằm bên phải trục Oy.
- Tương tự, miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox nằm bên trên trục Ox.
- Miền nghiệm D3 của bất phương trình x + y ≤ 100:
+ Vẽ đường thẳng d1: x + y = 100.
+ Vì 0 + 0 ≤ 100 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 100.
Do đó, miền nghiệm D3 của bất phương trình x + y ≤ 100 là nửa mặt phẳng bờ d1 chứa gốc tọa độ O.
- Miền nghiệm D4 của bất phương trình 2x + y ≤ 120:
+ Vẽ đường thẳng d2: 2x + y = 120.
+ Vì 2. 0 + 0 ≤ 120 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình 2x + y ≤ 120.
Do đó, miền nghiệm D4 của bất phương trình 2x + y ≤ 120 là nửa mặt phẳng bờ d2 chứa gốc tọa độ O.
Từ đó ta có miền nghiệm tô màu xanh chính là giao miền nghiệm của các bất phương trình trong hệ.
Miền nghiệm là miền tứ giác OABC với O(0;0), A(0;100), B(20;80) và C(60;0).
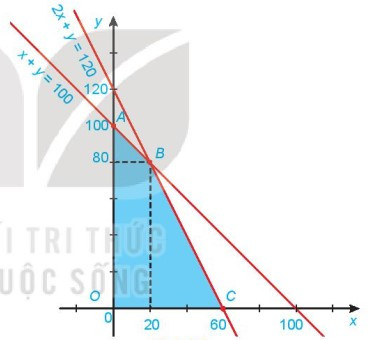
Bước 2: Tính giá trị của biểu thức F tại các đỉnh của tứ giác
F(O) = 0; F(A) = 200; F(B) = 230; F(C) = 210.
Bước 3: So sánh các giá trị thu được ở Bước 2, kết luận giá trị lớn nhất của F(x;y) là 230.
Các dạng bài tập Bất phương trình bậc nhất hai ẩn
(Xem trong file đính kèm)
Hệ thống bài tập
Dạng 1: Các bài toán biểu diễn bất phương trình bậc nhất hai ẩn
Dạng 2: Các bài toán hệ bất phương trình bậc nhất hai ẩn
Dạng 3: Các bài toán thực tiễn
Hệ thống bài tập trắc nghiệm
Dạng 1. Tìm nghiệm bất phương trình bậc nhất hai ẩn.
Dạng 2. Tìm miền nghiệm của hệ bất phương trình bậc nhất hai ẩn.
Dạng 3. Tìm giá trị nhỏ nhất- giá trị lớn nhất.
Dạng 4. Áp dụng bài toán thực tiễn.
Bài tập tự luyện
1. Bài tập vận dụng
1.1. Bài tập tự luận
Bài 1. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
a) {x<0y>0 b){x2<0y>0 c) 2x+y>0 d) {x−y<0x+y>1010
Hướng dẫn giải
- Hệ bất phương trình {x<0y>0là hệ bất phương trình bậc nhất hai ẩn vì có 2 bất phương trình x < 0 và y
> 0 đều là bất phương trình bậc nhất hai ẩn.
- Hệ bất phương trình {x2<0y>0 không là hệ bất phương trình bậc nhất hai ẩn vì có bất phương trình
x2 < 0 không là bất phương trình bậc nhất hai ẩn.
- 2x + y > 0 không là hệ bất phương trình bậc nhất hai ẩn vì chỉ có một bất phương trình bậc nhất hai ẩn.
Hệ bất phương trình {x−y<0x+y>1010là hệ bất phương trình bậc nhất hai ẩn vì có 2 bất phương trình x – y
< 0 và x + y > 1010 đều là bất phương trình bậc nhất hai ẩn.
Vậy có hệ {x<0y>0 và {x−y<0x+y>1010 là hệ bất phương trình bậc nhất hai ẩn.
Bài 2. Cho hệ bất phương trình {x≥0y≥0x+y≤1202x+y≤180
a) Tìm 2 nghiệm của hệ trên.
b) Cho F(x;y)=2x+2y. Tìm giá trị lớn nhất của F(x;y).
Hướng dẫn giải
a) Chọn (x; y) = (1; 1).
Thay x = 1 và y = 1 vào bất phương trình x ≥ 0 ta được 1 ≥ 0 là mệnh đề đúng. Do đó cặp (1; 1) là nghiệm của bất phương trình x ≥ 0.
Thay x = 1 và y = 1 vào bất phương trình y ≥ 0 ta được 1 ≥ 0 là mệnh đề đúng. Do đó cặp (1; 1) là nghiệm của bất phương trình y ≥ 0.
Thay x = 1 và y = 1 vào bất phương trình x + y ≤ 120 ta được 1 + 1 ≤ 120 là mệnh đề đúng. Do đó cặp (1; 1) là nghiệm của bất phương trình x + y ≤ 120.
Thay x = 1 và y = 1 vào bất phương trình 2x + y ≤ 180 ta được 2. 1 + 1 ≤ 180 là mệnh đề đúng. Do đó cặp (1; 1) là nghiệm của bất phương trình 2x + y ≤ 180.
Vậy (x; y) = (1; 1) là nghiệm của hệ bất phương trình {x≥0y≥0x+y≤1202x+y≤180.
Tương tự ta chọn được (x; y) = (2; 2) thỏa mãn tất cả các bất phương trình trong hệ đã cho. Do đó (2; 2) là nghiệm của hệ bất phương trình {x≥0y≥0x+y≤1202x+y≤180.
Vậy 2 nghiệm của hệ trên là (1; 1) và (2; 2).
b)
- Xác định miền nghiệm D1 của bất phương trình x ≥ 0.
+ Đường thẳng x = 0 là trục tọa độ Oy.
+ Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy nằm bên phải trục Oy.
- Tương tự, miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox nằm bên trên trục Ox.
- Miền nghiệm D3 của bất phương trình x + y ≤ 120:
+ Vẽ đường thẳng d1: x + y = 120.
+ Vì 0 + 0 ≤ 120 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 120.
Do đó, miền nghiệm D3 của bất phương trình x + y ≤ 120 là nửa mặt phẳng bờ d1 chứa gốc tọa độ O.
- Miền nghiệm D4 của bất phương trình 2x + y ≤ 180:
+ Vẽ đường thẳng d2: 2x + y = 180.
+ Vì 2. 0 + 0 ≤ 180 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình 2x + y ≤ 180.
Do đó, miền nghiệm D4 của bất phương trình 2x + y ≤ 180 là nửa mặt phẳng bờ d2 chứa gốc tọa độ O.
Từ đó ta có miền nghiệm không bị gạch chính là giao miền nghiệm của các bất phương trình trong hệ.
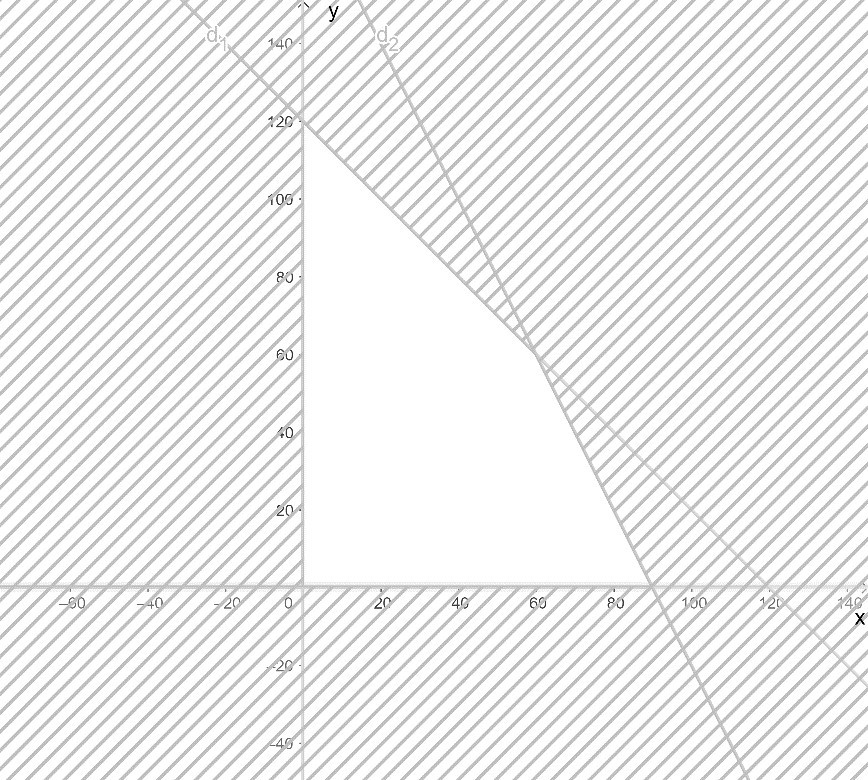
Bài 3. Cho hệ bất phương trình {x+2y<0x−4y>−6. Hỏi đây có phải hệ bất phương trình bậc nhất hai ẩn
không? Khi cho y = 0, x có thể nhận các giá trị nguyên nào?
Hướng dẫn giải
{x+2y<0x−4y>−6là hệ bất phương trình bậc nhất hai ẩn bởi vì có 2 bất phương trình x + 2y < < 0 và x – 4y
> - 6 là bất phương trình bậc nhất 2 ẩn.
Khi y = 0, hệ trở thành: {x<0x>−6⇔−6<x<0
Vậy x có thể nhận các giá trị nguyên là: {−5;−4;−3;−2;−1}.
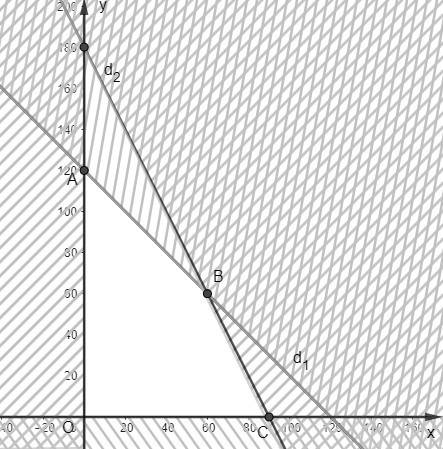
Miền nghiệm của hệ bất phương trình trên là miền tứ giác OABC với:
O(0;0), A(0;120), B(60;60), C(90;0).
Ta có: F(O) = 0; F(A) = 240; F(B) = 240; F(C) = 180.
Vậy giá trị lớn nhất của F(x;y) là 240 khi (x;y)=(60;60) hoặc (0;120).
1.2. Bài tập trắc nghiệm
Bài 4. Tìm khẳng định sai trong các khẳng định sau:
A. Hệ {x+y≥−1y2−1≤0không phải là hệ bất phương trình bậc nhất hai ẩn;
B. Hệ {x≥1+y5x+y<0là hệ bất phương trình bậc nhất hai ẩn;
C. Hệ {x+1+y>0x2+y<0là hệ bất phương trình bậc nhất hai ẩn;
D. Hệ {12x+2y<7x+3y≤0là hệ bất phương trình bậc nhất hai ẩn;
Hướng dẫn giải
Đáp án đúng là: C
+ Vì {x+y≥−1y2−1≤0chứa bất phương trình bậc hai y2 – 1 ≤ 0 nên hệ này không phải là hệ bất phương
trình bậc nhất hai ẩn.
Do đó khẳng định A đúng.
+ Vì {x≥1+y5x+y<0chứa hai bất phương trình x ≥ 1 + y và 5x + y < 0 đều là các bất phương trình bậc nhất
hai ẩn, nên hệ này là hệ bất phương trình bậc nhất hai ẩn.
Do đó khẳng định B đúng.
+ Vì {x+1+y>0x2+y<0chứa bất phương trình bậc hai x2 + y < 0 nên hệ này không phải là hệ bất phương
trình bậc nhất hai ẩn.
Do đó khẳng định C sai.
+ Vì {12x+2y<7x+3y≤0chứa hai bất phương trình 12x+y<7 và x + 3y ≤ 0 đều là các bất phương trình bậc
nhất hai ẩn nên hệ này là hệ bất phương trình bậc nhất hai ẩn.
Do đó khẳng định D đúng.
Vậy ta chọn đáp án C.
Bài 5. Cặp số (0; –3) là nghiệm của hệ bất phương trình nào sau đây?
A. {x−y≤1x+3y≤3x−4
B. {2x−y>02x+y>1
C. {−x−4y>−32x+y≤2
D. {2x−y≤−35y≥−1
Hướng dẫn giải
Đáp án đúng là: C
+ Ta có: 0 – (–3)= 3 > 1 và 0 + 3. (–3) < 3.0 – 4 (–9 < –4) là mệnh đề đúng.
Do đó cặp số (0; –3) không là nghiệm của bất phương trình x – y ≤ –1.
Vậy nên cặp số (0; –3) không là nghiệm của hệ bất phương trình{x−y≤1x+3y≤3x−4.
+ Ta có: 2.0 – (–3)= 3 > 0 và 2.0 + (–3) = – 3 < 1.
Do đó cặp số (0; –3) không là nghiệm của bất phương trình 2x + y > 1.
Vậy nên cặp số (0; –3) không là nghiệm của hệ bất phương trình{2x−y>02x+y>1.
+ Ta có: –0 – 4.(–3)= 12 > – 3 và 2.0 + (–3) = – 3 < 2.
Do đó cặp số (0; –3) là nghiệm của cả hai bất phương trình –x –4y > –3 và 2x + y ≤ 2.
Vậy nên cặp số (0; –3) là nghiệm của hệ bất phương trình{−x−4y>−32x+y≤2.
+ Ta có: 2.0 – (–3)= 3 > – 3 và 5. (–3) = – 15 <– 1.
Do đó cặp số (0; –3) không là nghiệm của cả hai bất phương trình 2x – y ≤ –3 và 5y ≥ –1.
Vậy nên cặp số (0; –3) không là nghiệm của hệ bất phương trình{2x−y≤−35y≥−1.
Vậy nên cặp số (0; –3) là nghiệm của hệ bất phương trình{−x−4y>−32x+y≤2.
Do đó ta chọn đáp án C.
Bài 6. Miền không gạch chéo trong hình vẽ dưới đây (không chứa bờ), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
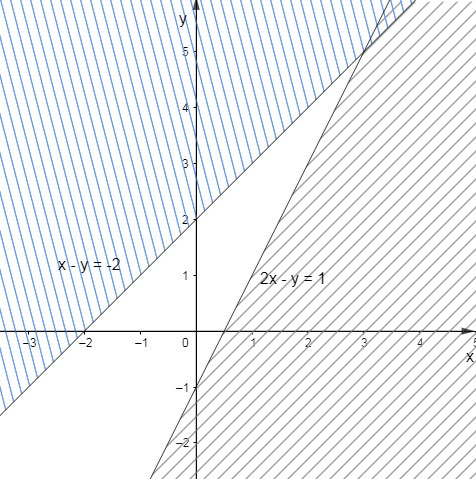
A. {x−y≥−22x−y≥1
B. {x−y>−22x−y<1
C. {x−y<−22x−y>1
D. {x−y<−22x−y<1
Hướng dẫn giải
Đáp án đúng là: B
Đường thẳng x – y = –2 chia mặt phẳng tọa độ thành hai nửa mặt phẳng.
Xét điểm O(0; 0), ta có: 0 – 0 = 0 > –2 .
Mặt khác điểm O thuộc miền nghiệm của hệ bất phương trình cần tìm. Do đó ta có bất phương trình thứ nhất của hệ là x – y > –2.
Đường thẳng 2x – y = 1 chia mặt phẳng tọa độ thành hai nửa mặt phẳng.
Xét điểm O(0; 0), ta có: 2.0 – 0 = 0 < 1 .
Mặt khác điểm O thuộc miền nghiệm của hệ bất phương trình cần tìm. Do đó ta có bất phương trình thứ hai của hệ là 2x – y < 1.
Suy ra hệ cần tìm là: {x−y>−22x−y<1
Ta chọn đáp án B.
2. Bài tập tự luyện có hướng dẫn
(Xem thêm trong file đính kèm)
Xem thêm các dạng bài tập liên quan khác:
200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)
100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)
500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2023)
60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024) có đáp án
300 Bài tập Toán 8 chương 4: Bất phương trình bậc nhất một ẩn (có đáp án năm 2023)